Kütle ve Ağırlık Merkezi 11. Sınıf Fizik
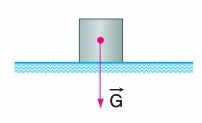
Ağırlık, bir cisme etki eden yerçekimi kuvvetidir. Yönü daima yerin merkezine doğru olan vektörel bir büyüklüktür. Büyüklüğü; G = m. g dir. Burada,
G: Cismin ağırlığı
m: Cismin kütlesi
g: Yerçekimi ivmesidir.
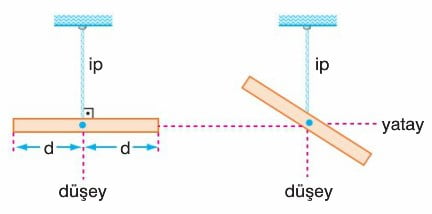
Bir cismin her birim kütlesine etkiyen yerçekimi kuvvetlerinin bileşkesinin uygulama noktasına ağırlık merkezi denir. Cismin kütle merkezi de aynı noktada tanımlanabilir.
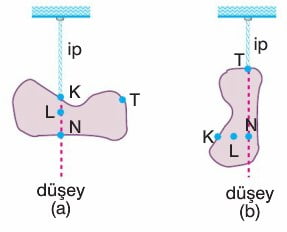
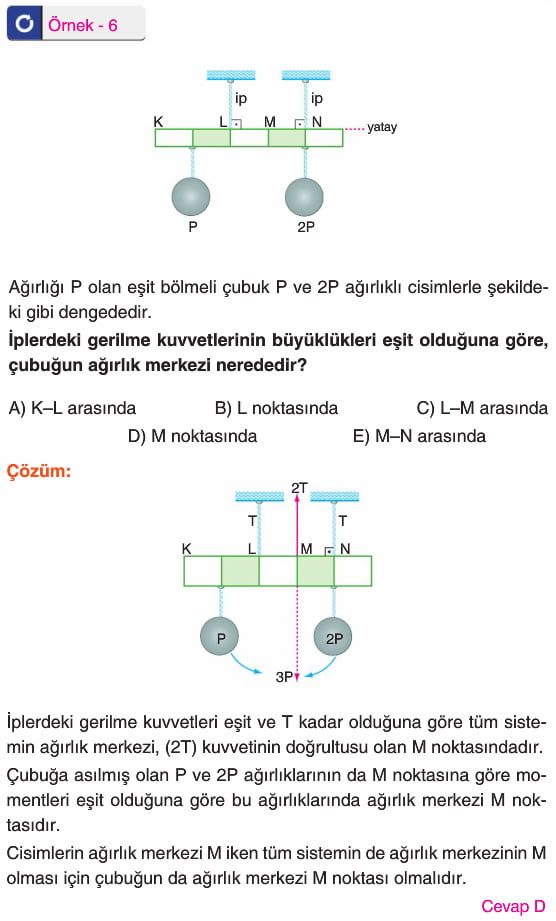
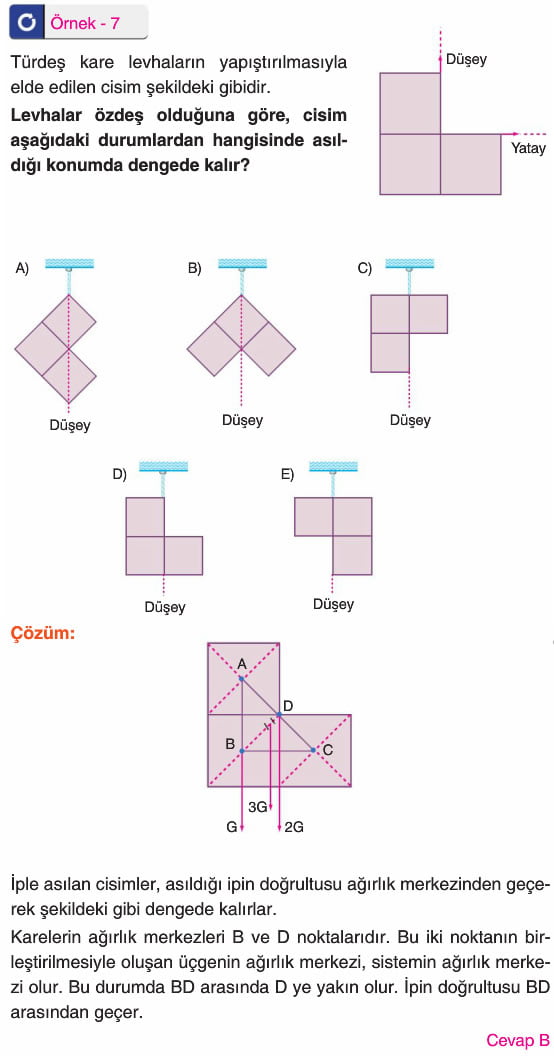
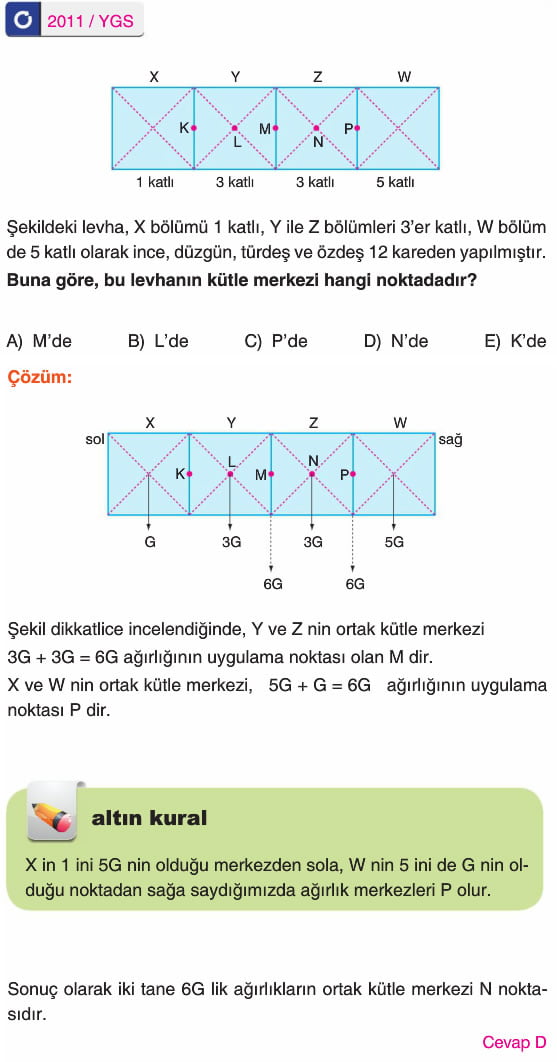
Ağırlık merkezinden asılan tüm cisimler, asıldıkları konumda dengede kalır. Ağırlık merkezinden asılmazsa, ipin uzantısı ağırlık merkezinden geçerek şekildeki gibi dengede kalır. (a) ipin uzantısı K, L, N noktalarının üstünden geçtiğinden bu noktalar ağırlık merkezi olabilir. (b) ipin uzantısı T, N noktalarının üstünden geçtiğinden, (a) daki yorumdan da N noktasının ağırlık merkezi olduğu bulunur.
Bazı Türdeş ve Geometrik Cisimlerin Ağırlık Merkezi
1. Türdeş çubuğun ağırlık merkezi orta noktasıdır.
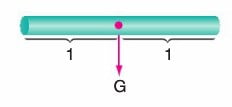
2. Türdeş çember, daire ve kürenin ağırlık merkezleri kendi geometrik merkezleridir.
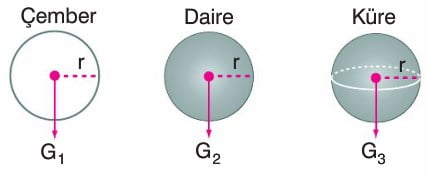
3. Düzgün ve türdeş kare, dikdörtgen, paralelkenar ve eşkenar dörtgen şeklindeki tellerin ve levhaların ağırlık merkezi köşegenlerin kesişim noktasıdır.
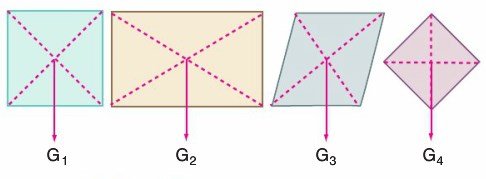
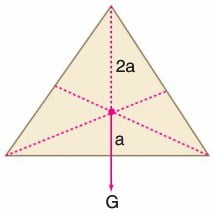
4. Türdeş üçgen şeklindeki levhanın ağırlık merkezi kenarortaylarının kesim noktasıdır.
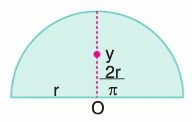
5. Yarım çemberin ağırlık merkezi, yarım çember şeklinde kıvrılmış bir telin ağırlık merkezi, O noktasından ğ uzaklıktaki y noktasındadır.
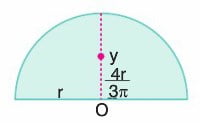
6. Yarım daire şeklindeki levhanın ağırlık merkezi, O noktasından y= 4r / 3pi uzaklıktaki y noktasındadır.
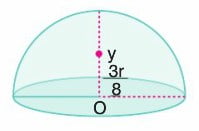
7. Yarım küre şeklindeki cismin ağırlık merkezi, şekildeki O noktasından y = g uzaklıktaki y noktasındadır.
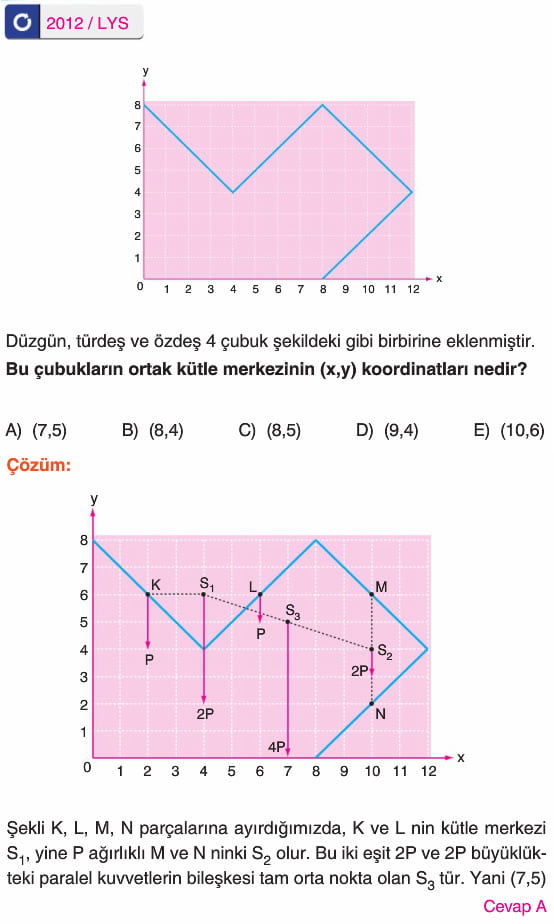
Ağırlık Merkezinin Koordinatları
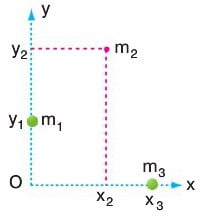
Aynı düzlemde bulunan birden çok cisimden oluşmuş sistemin ağırlık merkezi, cisimlerin ağırlıklarının herhangi bir noktaya göre torklarının toplamı, toplam ağırlığın aynı noktaya göre torkuna eşitlenerek bulunabilir.
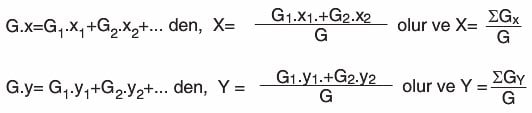
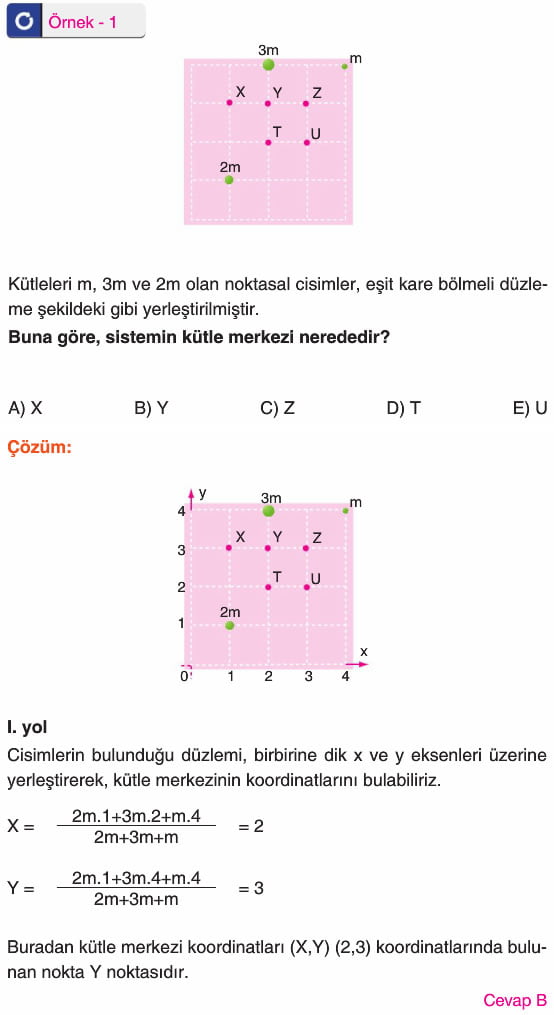
Ağırlık için yazılan bağıntı kütle için de geçerli olur. Dolayısıyla; Şekildeki m1, m2 ve m3 kütlelerinin kütle merkezinin koordinatları:
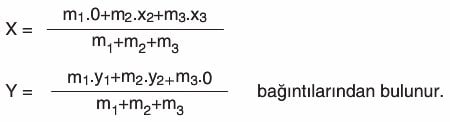
Not: Bu tip sorularda, kütle merkezinin koordinatları bulunarak ta sonuca gidilebilir. Ayrıca kütlelerin ikişerli kütle merkezlerini bulup çözüm yapılabilir.
Taktik: Kütle değerleri uygun verildiğinde bu sorudaki gibi, kütlelerin ikişer ikişer kütle merkezlerini bulabiliriz. Örneğin; 2m ve m kütlelerinin merkezi T noktasıdır. Burada 3m kütleli cisim olduğu varsayılarak, bu cisimle, 3m kütleli cismin merkezi Y noktası olur.
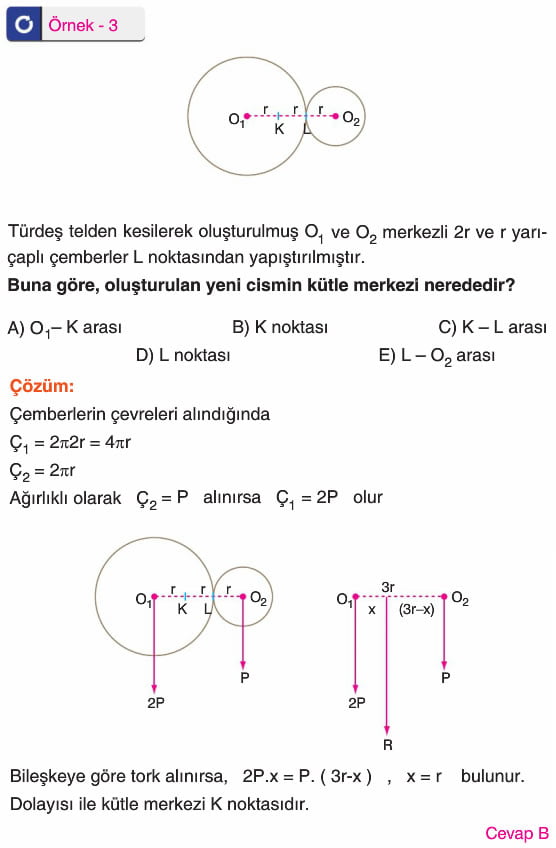
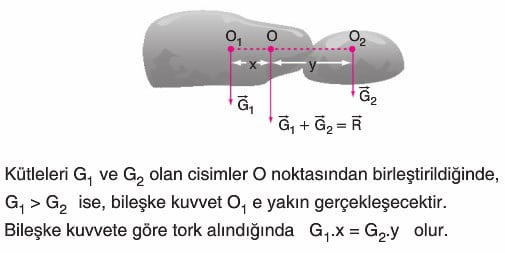
Birleştirilmiş Cisimlerin Kütle Merkezinin Bulunması
Basit Makineler konusuna gitmek için tıklayın.
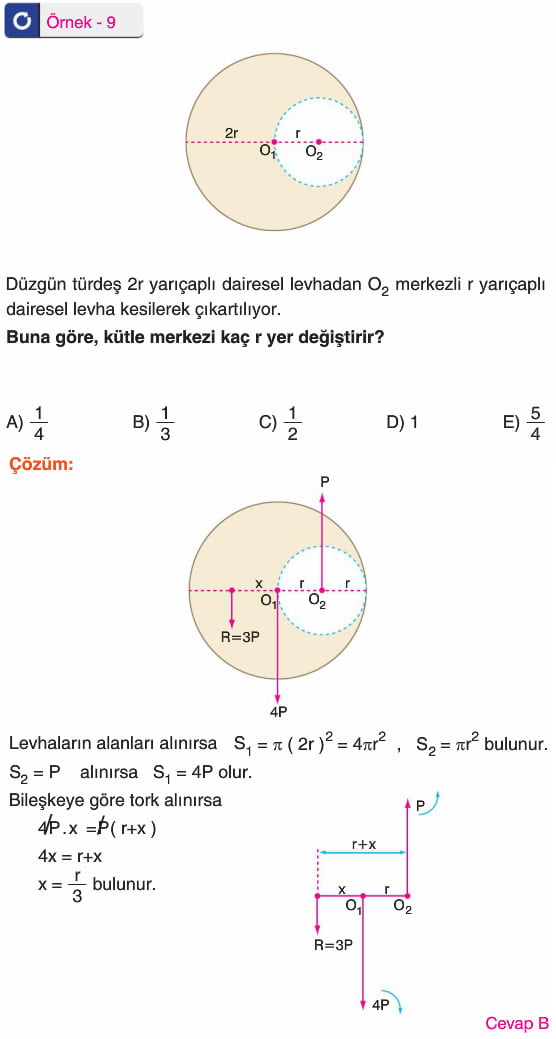
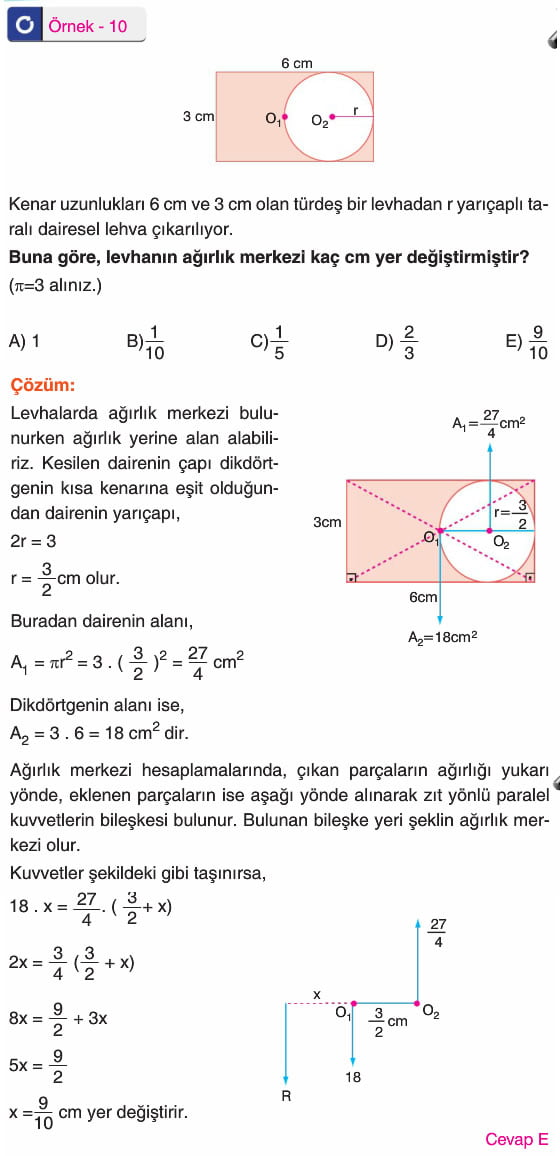
İçinden Parça Çıkarılan Cisimlerin Ağırlık Merkezinin Bulunması
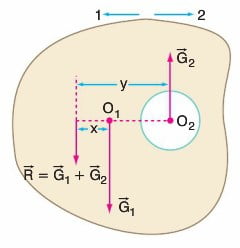
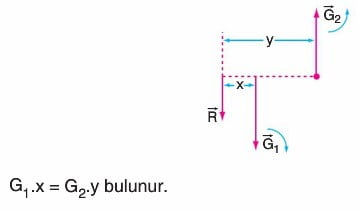
01 merkezli cisimden o2 merkezli parça çıkarıldığında sistemin kütle merkezi o1 den x kadar 1 yönüne kayar. Bileşkeye göre tork alındığında,
Çözümlü Örnek Test Soruları: Kütle ve Ağırlık Merkezi
1. Homojen bir çubuğun kütle merkezi neresindedir?
A) Çubuğun uç noktasında
B) Çubuğun tam ortasında
C) Çubuğun herhangi bir yerinde
D) Çubuğun ağırlık merkezinde
Çözüm:
Homojen bir çubuğun kütle yoğunluğu her yerde aynı olduğundan, kütle merkezi çubuğun tam ortasındadır.
Doğru cevap: B
2. Bir dikdörtgen levhanın kütle merkezi nerededir?
A) Köşegenlerin kesişim noktasında
B) Bir kenarın orta noktasında
C) Bir köşesinde
D) Herhangi bir noktada
Çözüm:
Homojen bir dikdörtgen levhanın kütle merkezi, köşegenlerin kesişim noktasında bulunur.
Doğru cevap: A
3. Aşağıdaki cisimlerden hangisinin ağırlık merkezi belirtilen yerindedir?
A) Üçgenin kenar orta noktalarında
B) Çemberin herhangi bir noktasında
C) Kürenin merkezinde
D) Düzgün dairenin herhangi bir noktasında
Çözüm:
Düzgün bir kürenin ağırlık merkezi, her zaman merkezinde yer alır.
Doğru cevap: C
4. Aşağıdaki ifadelerden hangisi kütle merkezi için doğrudur?
A) Kütle merkezi her zaman cismin içinde bulunur.
B) Cisim düzensiz ise kütle merkezi dışında olabilir.
C) Kütle merkezi, yalnızca düzgün cisimler için tanımlanır.
D) Kütle merkezi ile ağırlık merkezi farklıdır.
Çözüm:
Düzensiz şekilli bir cismin kütle merkezi, cismin dışında bir noktada yer alabilir.
Doğru cevap: B
5. Bir masa gibi düzgün olmayan cisimlerde ağırlık merkezini bulmak için hangi yöntem kullanılır?
A) Çubuğun tam ortasına bakılır.
B) Cismin herhangi bir köşesi seçilir.
C) Asma yöntemi uygulanır.
D) Üst kenarına kuvvet uygulanır.
Çözüm:
Düzgün olmayan cisimlerin ağırlık merkezini bulmak için asma yöntemi kullanılır. Bu yöntemde, cisim birkaç farklı noktadan asılır ve ağırlık merkezinin konumu belirlenir.
Doğru cevap: C
6. Ağırlık merkezi ve kütle merkezi aynı olan bir cisim için hangisi doğrudur?
A) Cisim homojen olmalıdır.
B) Cisim düzensiz şekilli olmalıdır.
C) Cisim yalnızca sıvı olmalıdır.
D) Ağırlık merkezi cisim dışında yer almalıdır.
Çözüm:
Ağırlık merkezi ve kütle merkezi aynı olan bir cisim homojen ve düzenli bir yapıya sahip olmalıdır.
Doğru cevap: A