Kümeler İle İlgili Temel Kavramlar 9. sınıf
Küme Kavramı
Küme, aynı özellikleri taşıyan iyi tanımlanmış nesneler topluluğudur. Yapılan tanım herkes tarafından aynı şekilde anlaşılmıyorsa iyi tanımlanmış olmaz.
Örneğin, “sınıftaki gözlüklü öğrenciler” ifadesi iyi tanımlandığı için bir küme belirtir. Fakat “haftanın bazı günleri” ifadesi iyi tanımlanmadığı için bir küme belirtmez.

Kümenin Elemanları ve Eleman Sayısı
Bir kümeyi oluşturan nesnelere o kümenin elemanları denir.
- Kümeler A, B, … gibi büyük harflerle gösterilir.
- Bir A kümenin eleman sayısı s(A) şeklinde gösterilir.
- Eğer x elemanı, A kümesinin elemanı ise x ∈ A,
- Eğer x elemanı, A kümesinin elemanı değilse x ∉ A,
şeklinde gösterilir.
Örneğin, A kümesi “36 yı bölen asal sayılar” şeklinde tanımlanırsa A kümesinin elemanları 2 ve 3 olur.
2 ∈ A, 3 ∈ A, 5 ∉ A şeklinde yazılır.
s(A) = 2 dir.
Küme Gösterim Yöntemleri
Liste Yöntemi

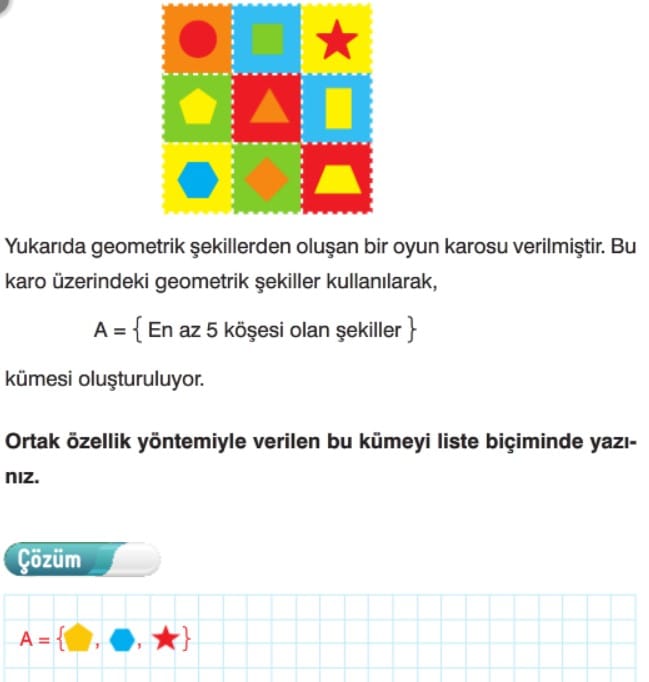
Ortak Özellik Yöntemi

Venn Şeması



Boş Küme

Çözümlü Sorular
Eşit Küme

Sonlu ve Sonsuz Küme

Evrensel Küme



Kümeler İle İlgili Temel Kavramlar Çözümlü Sorular
Kümeler Online Testler Tıklayın
Kümelerle İlgili Temel Kavramlar konusundan sonra gelen konular ise Alt Küme ve Eşit Kümeler konularıdır. Bu konulara gitmek için aşağıdaki bağlantılara tıklayabilirsiniz.
Kümelerde Temel Kavramlar Konuları
- Kümeler ile İlgili Temel Kavramlar
→ Kümeler ile İlgili Temel Kavramlar Soru Çözümleri - Alt Küme
→ Alt Küme Soru Çözümleri - Eşit Kümeler ve Soruları
Çözümlü Test Soruları
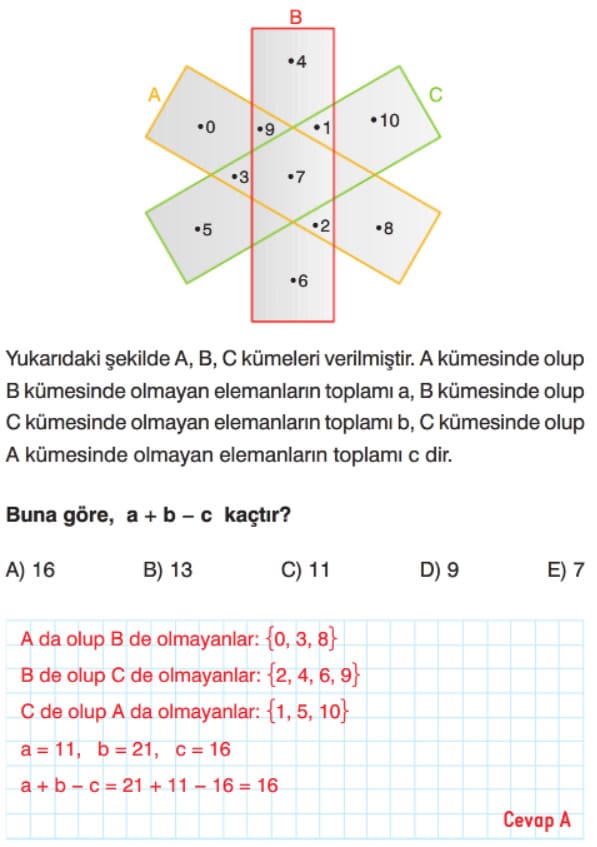
1. A = {2, 4, 6, 8} ve B = {4, 8, 10, 12} kümeleri veriliyor. A ∩ B (A kesişim B) kümesi aşağıdakilerden hangisidir?
A) {2, 6}
B) {4, 8}
C) {10, 12}
D) {2, 4, 6, 8, 10, 12}
Cevap: B (A ve B kümelerinde ortak olan elemanlar {4, 8}’dir.)
2. A = {x | x bir rakamdır} kümesi kaç elemanlıdır?
A) 8
B) 9
C) 10
D) 11
Cevap: C (Rakamlar {0,1,2,3,4,5,6,7,8,9} olduğundan kümede 10 eleman vardır.)
3. Evrensel küme E = {1, 2, 3, 4, 5, 6, 7, 8, 9} ve A = {2, 4, 6, 8} kümesi veriliyor. A kümesinin tümleyeni A’ aşağıdakilerden hangisidir?
A) {1, 3, 5, 7, 9}
B) {2, 4, 6, 8}
C) {1, 2, 3, 4, 5, 6, 7, 8, 9}
D) {1, 2, 3, 5, 7}
Cevap: A (A’nın tümleyeni, Evrensel Küme’de olup A’da olmayan elemanlardır: {1, 3, 5, 7, 9}.)
4. A = {a, b, c, d} ve B = {b, d, e, f} kümeleri veriliyor. A ∪ B (A birleşim B) kümesi aşağıdakilerden hangisidir?
A) {a, b, c, d}
B) {b, d, e, f}
C) {a, b, c, d, e, f}
D) {a, c, e, f}
Cevap: C (A ve B kümelerindeki tüm elemanlar yazılır: {a, b, c, d, e, f}.)
5. Boş küme ile ilgili aşağıdakilerden hangisi yanlıştır?
A) Boş küme {} ile gösterilir.
B) Boş kümenin eleman sayısı sıfırdır.
C) Her küme boş kümeyi kapsar.
D) Boş kümenin en az bir elemanı vardır.
Cevap: D (Boş kümenin hiç elemanı yoktur, bu yüzden bu ifade yanlıştır.)
1. Boş küme her kümenin alt kümesidir. Herhangi bir A kümesi için Ø ⊂ A dır.
• Tanım gereği, boş kümenin elemanı yoktur. Boş kümenin elemanı olmadığından A kümesinden farklı bir elemanı da olamaz. A kümesinden farklı en az bir elemanı olmadığından boş küme her A kümesinin alt kümesidir.
2. Her küme evrensel kümenin alt kümesidir. Herhangi bir A kümesi için A ⊂ E dir.
• Tanım gereği, evrensel küme A kümesindeki tüm elemanları içerir. Yani A kümesinin her elemanı evrensel kümenin de elemanıdır. Alt küme tanımından her A kümesi evrensel kümenin alt kümesi olur.
3. Her küme kendisinin alt kümesidir. Herhangi bir A kümesi için A ⊂ A dır.
• A kümesinin her elemanı kendisinin de elemanıdır. Dolayısıyla A kümesinin kendisinden farklı elemanı yoktur. O hâlde her A kümesi kendisinin alt kümesi olur.
4. Herhangi A, B, C kümesi için A kümesi B kümesinin, B kümesi de C kümesinin alt kümesi ise A kümesi de C kümesinin alt kümesidir.
A ⊂ B, B ⊂ C ise A ⊂ C olur.
• A ⊂ B ise A kümesinin her elemanı B kümesinin elemanıdır. B⊂ C ise B kümesinin her elemanı C kümesinin de elemanıdır. O hâlde A
kümesinin her elemanı C kümesinin de elemanı olur. Bu durumda herhangi A, B, C kümeleri için A ⊂ B, B ⊂ C ise A ⊂ C dir.
Augustus De MORGAN (1806-1871)
Augustus De MORGAN (Ougıst De Morgın) asker bir babanın çocuğu olarak Hindistan’da doğmuştur. Çocukluk çağlarında arkadaşlarıyla fiziksel bozukluğu nedeniyle problem yaşamıştır. Augustus De Morgan, 1823 yılında Londra’dan ayrılarak Trinity College Cambridge’te (Trinity Kolej Kambriç) öğrenimine devam etmiştir. Burada üç yıl okumuş ardından Londra’ya geri dönerek yeni açılan Londra Üniversitesi matematik bölümüne öğretim üyesi olarak kabul edilmiştir. Bu tarihte De Morgan’ın henüz bir matematik yayını olmamasına rağmen kazandığı bu sıfat De Morgan’ın dehasını gösterir. De Morgan, özellikle cebire getirdiği yeni yaklaşımlarla başarılı olmuş ve cebirin saf doğasını anlamayı başarmıştır. Kendi adını taşıyan ve kümelerin bileşim ve kesişimini içeren De Morgan kuralları ile matematiksel mantığın en önemli ismi olmayı başarmıştır.