Bu yazımızda Küme Problemleri konu anlatımı ve çözümlü örnekler bulunmaktadır. Çözümlü sorular için Küme problemleri soru çözümleri yazımıza gidebilirsiniz.

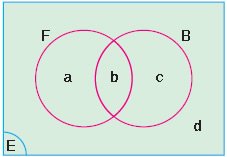
Futbol oynayanların kümesi: F
Basketbol oynayanların kümesi: B
a, b, c, d içinde bulundukları kümelerin eleman sayılarını göstersin.

Futbol oynayanların sayısı = a + b
Basketbol oynayanların sayısı = b + c
Sadece futbol oynayanların sayısı = a
Sadece basketbol oynayanların sayısı = c
Futbol ve basketbol oynayanların sayısı = b
Futbol veya basketbol oynayanların sayısı = a + b + c
Hiçbir oyun oynamayanların sayısı = d
En az bir oyun oynayanların sayısı = a + b + c
En çok bir oyun oynayanların sayısı = a + c + d

Küme Problemleri çözümlü örnekler

Kümeler Online Testler Tıklayın

Çözümlü Örnek Test Soruları: Küme Problemleri

Soru 1
Bir sınıfta 20 öğrenci futbol, 15 öğrenci basketbol, 10 öğrenci ise her iki sporu da yapmaktadır. Sınıfta toplam 30 öğrenci olduğuna göre, sadece futbol oynayan öğrenci sayısı kaçtır?
A) 5
B) 10
C) 15
D) 20

Çözüm
Her iki sporu yapan öğrenci sayısı 10’dur. Sadece futbol oynayan öğrenci sayısı, futbol oynayanlardan her iki sporu yapanlar çıkarılarak bulunur:
S(A) – S(A ∩ B) = 20 – 10 = 10.
Doğru cevap: B

Soru 2
Bir şehirde 100 kişi, 60 kişi gazete A’yı, 50 kişi gazete B’yi okumaktadır. Gazete A ve gazete B’yi birlikte okuyan 20 kişi olduğuna göre, yalnız bir gazete okuyan kişi sayısı kaçtır?
A) 70
B) 80
C) 90
D) 100

Çözüm
Yalnız bir gazete okuyanlar: (S(A) – S(A ∩ B)) + (S(B) – S(A ∩ B)) = (60 – 20) + (50 – 20) = 40 + 30 = 70.
Doğru cevap: A

Soru 3
Bir sınıfta 25 öğrenci matematik, 20 öğrenci fizik, 10 öğrenci ise her iki dersi de sevmektedir. Matematik veya fizik derslerinden en az birini seven öğrenci sayısı kaçtır?
A) 30
B) 35
C) 40
D) 45

Çözüm
Birleşim formülü:
S(A ∪ B) = S(A) + S(B) – S(A ∩ B).
S(A ∪ B) = 25 + 20 – 10 = 35.
Doğru cevap: B

Soru 4
40 kişilik bir grupta 25 kişi tenis, 15 kişi yüzme, 10 kişi ise her iki sporu yapmaktadır. Bu grupta sadece yüzme yapan kaç kişi vardır?
A) 5
B) 10
C) 15
D) 20

Çözüm
Sadece yüzme yapanlar:
S(B) – S(A ∩ B) = 15 – 10 = 5.
Doğru cevap: A

Soru 5
Bir ankette 50 kişi, 30 kişi kahve, 25 kişi çay içmektedir. Hem çay hem kahve içen kişi sayısı 15’tir. Yalnızca kahve içen kişi sayısı kaçtır?
A) 10
B) 15
C) 20
D) 25

Çözüm
Yalnızca kahve içenler:
S(A) – S(A ∩ B) = 30 – 15 = 15.
Doğru cevap: B

Soru 6
Bir dernekte 40 üyenin 20’si İngilizce, 15’i Fransızca, 5’i ise her iki dili de konuşmaktadır. Yalnızca İngilizce konuşan kişi sayısı kaçtır?
A) 10
B) 15
C) 20
D) 25

Çözüm
Yalnızca İngilizce konuşanlar:
S(A) – S(A ∩ B) = 20 – 5 = 15.
Doğru cevap: B

Soru 7
Bir okulda 80 öğrenci spor yapmaktadır. 50’si futbol, 40’ı voleybol, 20’si ise her iki sporu yapmaktadır. Hiçbir spor yapmayan öğrenci yoksa, okulda toplam kaç öğrenci vardır?
A) 100
B) 110
C) 120
D) 130

Çözüm
S(A ∪ B) = S(A) + S(B) – S(A ∩ B).
S(A ∪ B) = 50 + 40 – 20 = 70.
Sadece spor yapan öğrenci sayısı 70’tir. Toplam öğrenci sayısı 80 olduğundan: 80 – 70 = 10.
Doğru cevap: A

Soru 8
Bir sınıfta 30 öğrenci müzik, 25 öğrenci resim, 15 öğrenci ise her iki kulübe üye. Her iki kulübe üye olmayan kaç öğrenci vardır?
A) 5
B) 10
C) 15
D) 20

Çözüm
S(A ∪ B) = S(A) + S(B) – S(A ∩ B).
S(A ∪ B) = 30 + 25 – 15 = 40.
Toplam öğrenci sayısı: 40 – 15 = 25.
Doğru cevap: C

Küme Problemleri konu anlatımı videoları

Küme Problemleri Fem Akademi

• Küme problemleri çözülürken önce verilenlere uygun bir Venn Şeması çizilir. Sonra, kesişim bölgelerinden başlanarak eleman sayıları ile ilgili bölgelere yazılır. Bundan sonra gerekli denklemler kurulup çözüme gidilir.

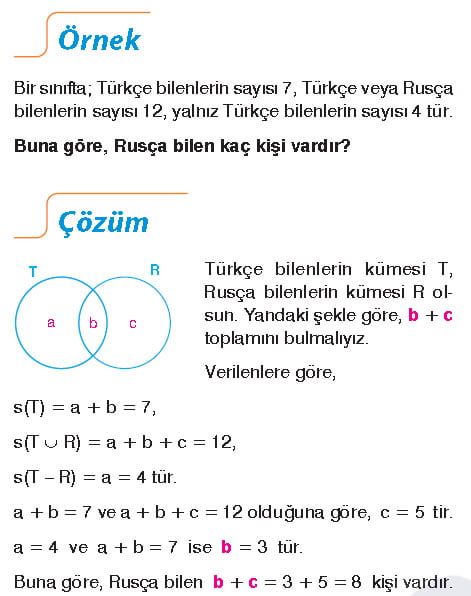
Soru: Bir sınıfta Türkçe bilenlerin sayısı 7, Türkçe ve Rusça bilenlerin sayısı 12, yalnız Türkçe bilenlerin sayısı 4 tür. Buna göre Rusça Bilen kaç kişi vardır. 29 kişinin bulunduğu bir sınıfta Türkçe dersinden geçen 15, matematik dersinden kalan 14 kişidir. Her iki dersten kalan 5 kişi olduğuna göre yalnız matematik dersinden geçen kaç kişi vardır?

Soru: 50 kişinin bulunduğu bir gezi grubunda yalnız Almanca ve yalnız Fransızca bilen kişi sayısı 35’tir. Gezi grubunda bu iki dili de bilmeyen kişi sayısı 10 olduğuna göre hem Almanca hem de Fransızca bilen kişi sayısı kaçtır?

Soru: En az bir dil bilenlerden oluşan bir turist kafilesinde 20 kişi Türkçe, 14 kişi Çince, 15 kişi Rusça konuşmaktadır. 8 kişi Türkçe ve Çince, 7 kişi Türkçe ve Rusça, 5 kişi Çince ve Rusça konuşmaktadır. Her üç dili konuşan 3 kişi olduğuna göre bu kafilede kaç kişi vardır?

Soru: Bir sınıftaki herkes futbol ve basketbol oyunlarından en az birini oynamaktadır. Futbol oynayanların sayısı 14, basketbol oynayanların sayısı 12, hem futbol hem de basketbol oynayanların sayısı 3 tür. Buna göre, bu sınıfta kaç öğrenci vardır?

Soru: 50 kişilik bir turist kafilesinde yalnız Çince bilenlerin sayısı yalnız Japonca bilenlerin sayısının 3 katıdır. Çince ve Japonca bilenlerin sayısı 4, Çince veya Japonca bilmeyenlerin sayısı 14 tür. Buna göre, bu turist kafilesinde Japonca bilen kaç kişi vardır?
Çözüm: Yalnız Japonca bilenlerin sayısına x denilirse yalnız Çince bilenlerin sayısı 3x olur. verilenler şemada şekildeki gibi gösterildikten sonra, tüm bölgelerdeki değerlerin toplamı 50 ye eşitlenir.

Soru: Satranç ve dama oyunlarından en az birini bilenlerin oluşturduğu 25 kişilik grupta satranç oynayanların sayısı dama oynayanların sayısının 2 katıdır. Bu grupta hem satranç hem de dama oynayan 8 kişi olduğuna göre, yalnız dama oynayan kaç kişi vardır?

Soru: Judo veya tekvando kursuna gidenlerden oluşan 16 kişilik bir grupta judo kursuna gidenlerin sayısı hem judo hem tekvando kursuna gidenlerin sayısının 3 katıdır. Yalnız Judo kursuna gidenlerin sayısı, tekvando kursuna gidenlerin sayısına eşit olduğuna göre, yalnız tekvando kursuna giden kaç kişi vardır?

Soru: Bir turist kafilesinde İngilizce, Türkçe ve Arapça dillerinden en az birini konuşabilenler vardır.
o İngilizce bilenler Türkçe ve Arapça konuşamamaktadır.
o Bu kafilede yalnız bir dil bilen 15 ve yalnız iki dil bilen 24 kişi vardır.
Buna göre, bu kafilede kaç kişi vardır?

Küme Problemleri konusu 9. sınıf matematik müfredatında Kümeler Ünitesinde Kümelerde İşlemler konusundan hemen sonra gelmektedir. Kümeler konusunda genellikle Ygs de 1 soru gelmektedir. Bu bir sorunun da küme problemlerinden gelme ihtimali oldukça yüksektir. Hazırladığımız bu yazımızda öncelikle text olarak küme problemleri konu anlatımını göreceksiniz. Bu yazdıklarımız yetersiz gelmişse eğer hemen altında farklı hocaların hazırladığı konu anlatımı videoları bulunmaktadır. Konunun en altında ise çözümlü örnekler yer almaktadır. Konu ile ilgili sorularınızı yorum yazarak bize gönderebilirsiniz.