Bu yazımızda Koşullu Önerme (İse Bağlacı) ve İki Yönlü Koşullu Önerme (Ancak ve Ancak Bağlacı) ders notları bulunmaktadır. Konuyu bitirdikten sonra Koşullu Önerme ve İki Yönlü Koşullu Soruları ve Çözümleri yazımıza gidebilirsiniz.
Sonraki Konu: Her ve Bazı Niceleyicileri

Koşullu Önerme

“Yağmur yağıyorsa bahçemizde yerler ıslaktır” önermesi p: “yağmur yağıyor” ve q: “bahçemizde yerler ıslak” önermelerinden elde edilmiş koşullu bir önermedir.

Yağmur yağdığında bahçemizde yerler ıslak olacağı için bu önerme doğru bir önermedir. Bu durumda “yağmur yağıyorsa, bahçemizde yerler ıslak değildir” önermesi yanlıştır. Çünkü bahçeye yağmur yağdığında yerler ıslak olur. Diğer yandan “yağmur yağmıyorsa bahçemizde yerler ıslaktır” önermesi de doğrudur. Çünkü bahçemizde yerlerin ıslak olması sadece yağmurun yağmasına bağlı değildir. “Yağmur yağmıyorsa bahçemizde yerler ıslak değildir” önermesi de doğrudur.

p ile q iki önerme olmak üzere,
p ise q koşullu bileşik önermesi “p ⇒ q” şeklinde gösterilir.

Bu önerme p doğru q yanlış iken yanlış, diğer durumlarda doğrudur.

p	q	p ⇒ q
1	1	1
1	0	0
0	1	1
0	0	1

ÖRNEK

p: “5 < 10” ile q: “-5 > -10” önermeleri için
p ⇒ q bileşik önermesini yazıp doğruluk değerini bulalım.

Çözüm:

p ⇒ q : “5 < 10” ⇒ “-5 > -10” dur.
5 < 10 olduğundan p önermesinin doğruluk değeri 1’dir.
-5 > -10 olduğundan q önermesinin de doğruluk değeri 1’dir.
Bu durumda p ⇒ q = 1 ⇒ 1 = 1 olur.

---

ÖRNEK

(p ∧ q’) ⇒ r = 0 olduğuna göre,
(p ∨ r) ⇒ q’ koşullu önermesinin doğruluk değerini bulalım.

Çözüm:

(p ∧ q’) ⇒ r = 0 olduğunda p ∨ q’ = 1 ve r = 0 olur.
p ∧ q’ = 1 ise p = 1 ve q’ = 1 dolayısıyla q = 0 olur.
O halde (p ∨ r) ⇒ q’ = (1 ∨ 0) ⇒ 1 = 1 bulunur.

ÖRNEK

p ∨ p’ ≡ q ve q ⇒ (p ∧ r’) = 1 olduğuna göre,
(p’ ∨ q) ∧ (p ∨ r) önermesinin doğruluk değerini bulalım.

Çözüm:

p ∨ p’ önermesinin doğruluk değeri 1 olduğundan
p ∨ p’ ≡ q ise q ≡ 1’dir. q ⇒ (p ∧ r’) ≡ 1 verildiğine göre,
1 ⇒ (p ∧ r’) ≡ 1 ise p ∧ r’ ≡ 1 olmalıdır.

p ∧ r’ ≡ 1 ise p ≡ 1 ve r’ ≡ 1 dolayısıyla p’ ≡ 0 ve r ≡ 0’dır.
O halde (p’ ∨ q) ∧ (p ∨ r) ≡ (0 ∨ 1) ∧ (1 ∨ 0) ≡ 1 ∧ 1 ≡ 1 bulunur.

---

BİLGİ

p ⇒ q koşullu önermesinin doğruluk değeri 1 ise bu koşullu önermeye gerektirme denir.

---

ÖRNEK

p ⇒ q : “x = 3 ⇒ x² = 9”

önermesinin bir gerektirme olup olmadığını inceleyelim.

Çözüm:

3² = 9 olduğundan “x = 3 ⇒ x² = 9” koşullu önermesi doğrudur. Bu durumda p ⇒ q : “x = 3 ⇒ x² = 9” önermesinin doğruluk değeri 1 olduğundan bu önerme bir gerektirmedir.

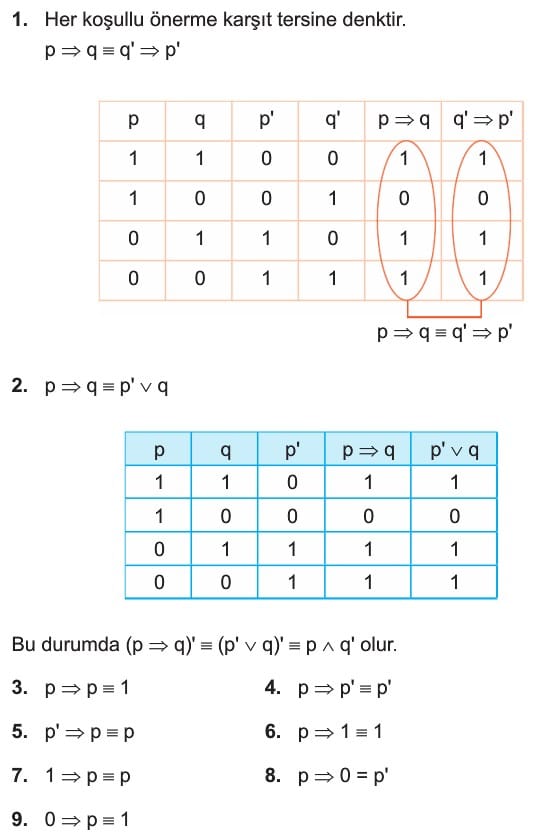
Koşullu Önermenin Karşıtı, Tersi, Karşıt Tersi

1. p ⇒ q koşullu önermesinin karşıtı, q ⇒ p koşullu önermesidir.
2. p ⇒ q koşullu önermesinin tersi, p’ ⇒ q’ koşullu önermesidir.
3. p ⇒ q koşullu önermesinin karşıt tersi, q’ ⇒ p’ koşullu önermesidir.

---

ÖRNEK

p : “a negatif tam sayıdır.”
q : “a³ negatif tam sayıdır.”

önermeleri veriliyor.

p ile q önermeleri için p ⇒ q koşullu önermesinin karşıtını, tersini ve karşıt tersini yazalım.

---

Çözüm:

Verilen önermelere göre,

• (p ⇒ q) : “a negatif tam sayı ise a³ negatif tam sayıdır.”
• Karşıtı, (q ⇒ p) : “a³ negatif tam sayı ise a negatif tam sayıdır.”
• Tersi, (p’ ⇒ q’) : “a negatif tam sayı değil ise a³ negatif tam sayı değildir.”
• Karşıt tersi, (q’ ⇒ p’) : “a³ negatif tam sayı değil ise a negatif tam sayı değildir.”

Koşullu Önermenin Özellikleri

İki Yönlü Koşullu Önerme

“Ancak ve ancak” bağlacı ile oluşturulan önermeye iki yönlü koşullu önerme denir. p ⇔ q biçiminde yazılır ve “p ancak ve ancak q” ya da “p gerek ve yeter şart q” diye okunur.

p ⇔ q önermesi p ⇒ q koşullu önermesi ile bunun karşıtı olan q ⇒ p koşullu önermesinin ∧ bağlacı ile bağlanmasından meydana gelir.

O halde, p ⇔ q ≡ (p ⇒ q) ∧ (q ⇒ p) yazılır.

p ve q önermeleri için p ⇔ q önermesinin doğruluk tablosu aşağıdaki gibidir.

Tablo incelendiğinde p ⇔ q önermesi, p ile q’nun doğruluk değerleri aynı iken doğru, farklı iken yanlıştır.

p	q	p ⇔ q
1	1	1
1	0	0
0	1	0
0	0	1

Verilen p ⇔ q iki yönlü koşullu önermesinin doğruluk değeri 1 ise bu önermeye çift gerektirme denir. Yani hem p ⇒ q, hem de q ⇒ p önermelerinin doğruluk değerleri 1 olursa çift gerektirme oluşur.

ÖRNEK

p : “m = 5’tir”
q : “3m – 2 = 13’tür”

önermeleri için p ⇔ q bileşik önermesini yazalım. Bu iki yönlü koşullu önermenin çift gerektirme olduğunu gösterelim.

---

Çözüm:

Verilen p ve q önermelerini iki yönlü koşullu önerme biçiminde yazarsak p ⇔ q : “m = 5 ancak ve ancak 3m – 2 = 13’tür” önermesi oluşur.

Bu iki yönlü koşullu önermenin çift gerektirme olduğunu gösterelim.

• m = 5 ise 3m – 2 = 13’tür.
  Çünkü:
  3 × 5 – 2 = 13
  15 – 2 = 13
  13 = 13
  dolayısıyla p ⇒ q = 1

• 3m – 2 = 13 ise m = 5’tir.
  Çünkü:
  3m = 13 + 2
  3m = 15
  m = 5 olur.
  q ⇒ p = 1

p önermesi için q yeter koşul, q önermesi de p için yeter koşul olduğundan p için gerek ve yeter koşul q’dur, dolayısıyla p ⇔ q önermesi çift gerektirmedir.

İki Yönlü Koşullu Önermenin Özellikleri

Koşullu Önerme ve İki Yönlü Koşullu Önerme Online Testler ve Çözümlü Sorular

 

Soru: “Meryem hasta ise okula gitmemiştir.” önermesinin karşıtı aşağıdakilerden hangisidir?
A) “Meryem hasta değilse okula gitmiştir.”
B) “Meryem okula gitmişse, hasta değildir.”
C) “Meryem hasta ise okula gitmiştir.”
D) “Meryem okula gitmişse, hastadır.”
E) “Meryem okula gitmemişse hastadır.”

Soru: p: “Hakan sınıftadır.”
q: “Murat sınıftadır.”
önermeleri veriliyor. Buna göre, p ise q önermesinin karşıt tersi aşağıdakilerden hangisidir?
A) Hakan sınıfta değilse, Murat sınıfta değildir.
B) Murat sınıfta değilse, Hakan sınıfta değildir.
C) Murat sınıfta ise, Hakan sınıftadır.
D) Hakan sınıfta ise Murat sınıftadır.
E) Hakan sınıfta değilse, Murat sınıftadır.

Soru: “Hava soğuk ise kar yağar.” önermesinin karşıt tersi aşağıdakilerden hangisidir?
A) Hava sıcak ise kar yağmaz.
B) Kar yağarsa hava soğuk olur.
C Hava soğuk değilse kar yağmaz.
D) Kar yağmazsa hava soğuk olmaz.
E) Kar yağmazsa hava soğuk olur.

Örnek Soru:
P: “Bir sayı pozitif.”
Q: “Sayının karesi pozitiftir.”
Bu durumu koşullu bir ifadeyle ifade edin ve doğruluğunu değerlendirin.
Çözüm: Koşullu Önerme: “Eğer bir sayı pozitifse, o zaman sayının karesi pozitiftir.” Bu durumda, P doğru olduğunda Q de doğrudur. Pozitif bir sayının karesi her zaman pozitiftir. Dolayısıyla, koşullu önerme doğrudur.

Örnek Soru:
P: “Bir doğal sayı tek bir sayıdır.”
Q: “Sayının karesi tekse, o sayı tek bir sayıdır.
Bu durumu iki yönlü koşullu bir ifadeyle ifade edin ve doğruluğunu değerlendirin.
Çözüm: İki Yönlü Koşullu Önerme: “Bir doğal sayı tek bir sayıdır, ve bir sayının karesi tekse, o sayı tek bir sayıdır.” Her iki yönlü ifade de doğrudur. Bir doğal sayı tekse, karesi de tek olacaktır; aynı şekilde bir sayının karesi tekse, o sayı tek olacaktır.