Kosinüs Teoremi ve Sinüs Teoremi 11. sınıf Matematik Ders Notu
Kosinüs Teoremi ve Sinüs Teoremi, 11. sınıf matematik müfredatında üçgenlerin kenar uzunlukları ve açıları arasındaki ilişkiyi anlamada kullanılan temel teoremlerdir. Kosinüs Teoremi, bir üçgenin herhangi bir açısını ve kenar uzunluklarını kullanarak üçüncü kenarı veya diğer açıları bulmamızı sağlar. Özellikle dik üçgenlerde Pisagor teoreminin genelleştirilmiş hali olarak kullanılır. Sinüs Teoremi ise, bir üçgenin açıları ve karşılarındaki kenar uzunlukları arasındaki orantıyı ifade eder ve üçgende bir açıyı veya kenarı bulmak için kullanılır. Bu iki teorem, üçgen çözümlemelerinde önemli bir yere sahiptir.
Kosinüs ve Sinüs Teoremi Testleri
Kosinüs Teoremi ve Sinüs Teoremi Ders notları
Kosinüs Teoremi
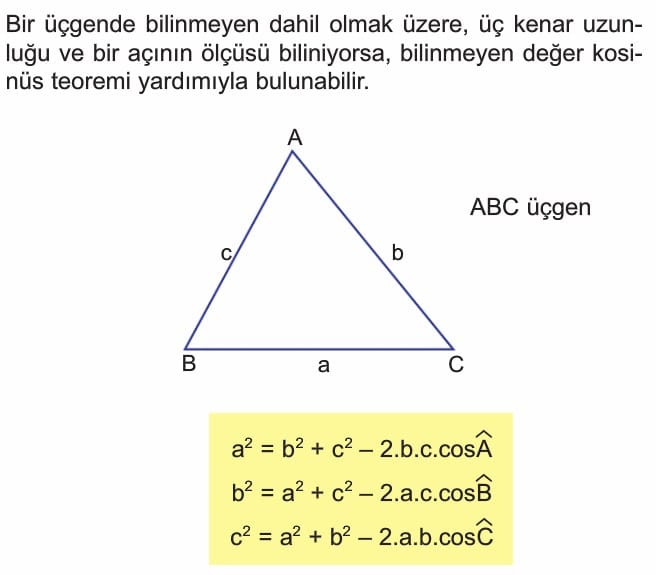
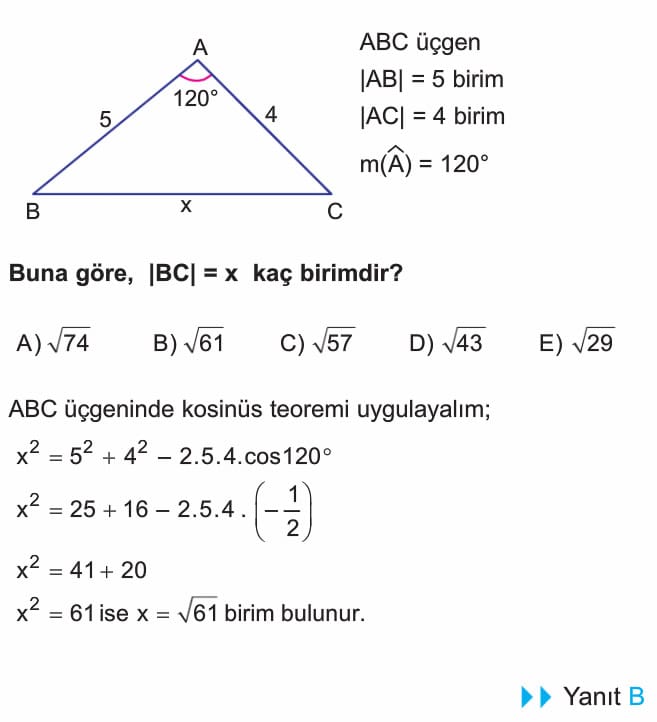
Örnek:
Sinüs Teoremi
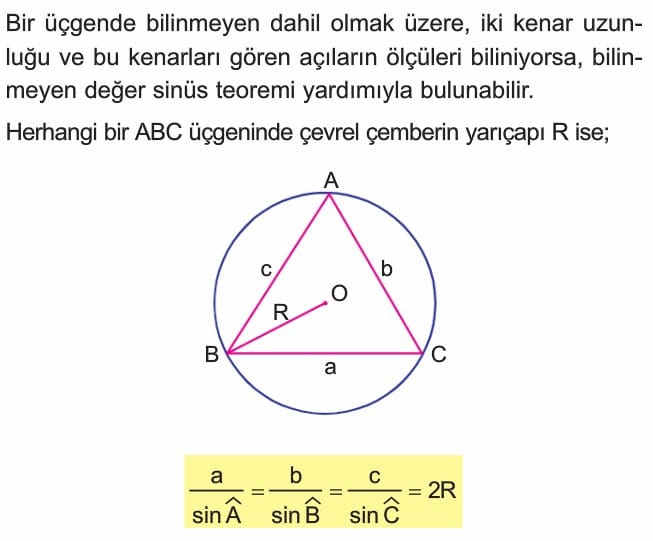
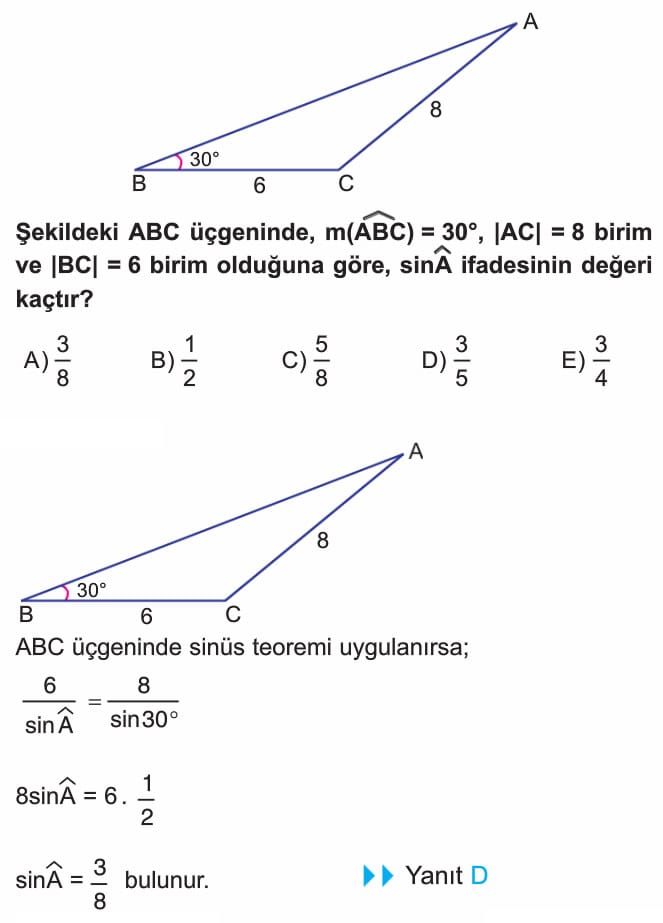
Örnek:
Üçgende Alan Formülleri
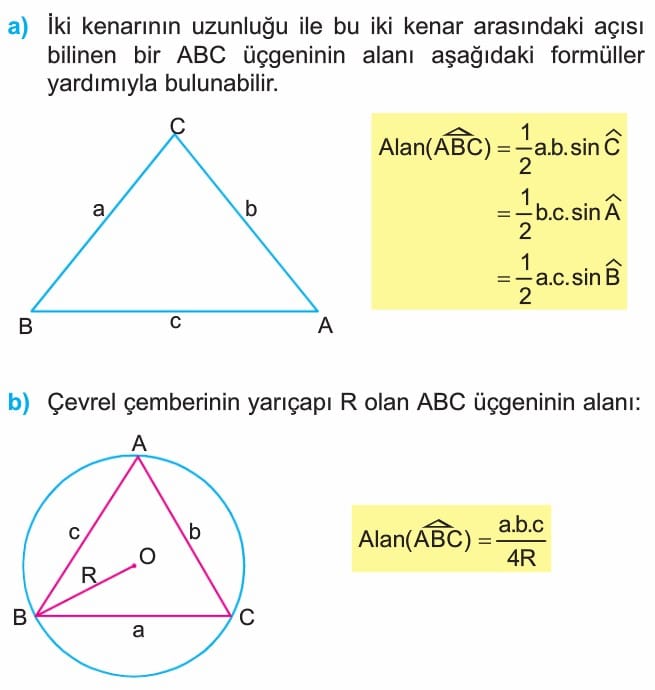
Örnek:
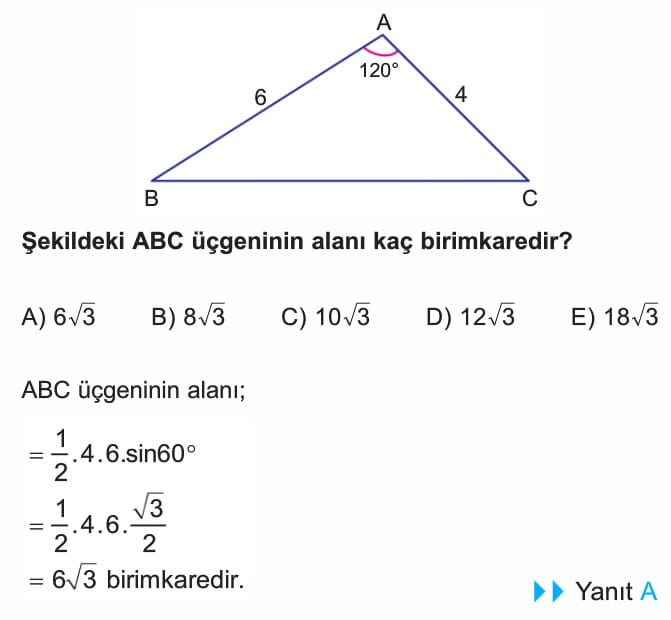
Kosinüs ve Sinüs Teoremi Çözümlü Sorular
1. ÜNİTE: TRİGONOMETRİ
- Yönlü Açılar
- Trigonometrik Fonksiyonlar
- Trigonometrik Özdeşlikler
- Kosinüs Teoremi ve Sinüs Teoremi
- Trigonometrik Fonksiyonların Periyotları
- Trigonometrik Fonksiyonların Grafikleri
- Ters Trigonometrik Fonksiyonlar
Çözümlü Test Soruları
Soru 1:
Bir üçgende, kenar uzunlukları 7 cm, 24 cm ve 25 cm’dir. Bu üçgenin dik üçgen olup olmadığını Kosinüs Teoremi’ni kullanarak belirleyiniz.
A) Evet, dik üçgendir.
B) Hayır, dik üçgen değildir.
C) Sadece 7 cm ve 24 cm kenarları dik açıyı oluşturur.
D) Sadece 24 cm ve 25 cm kenarları dik açıyı oluşturur.
E) Sadece 7 cm ve 25 cm kenarları dik açıyı oluşturur.
Çözüm: Kosinüs Teoremi’ne göre, eğer en uzun kenarın karesi diğer iki kenarın karelerinin toplamına eşitse, üçgen dik üçgendir.
25² = 625
7² + 24² = 49 + 576 = 625
625 = 625 olduğundan, üçgen dik üçgendir.
Doğru cevap: A) Evet, dik üçgendir.
Soru 2:
Bir üçgende iki kenarın uzunlukları sırasıyla 8 cm ve 15 cm’dir. Aralarındaki açı 60 derece olduğuna göre, üçüncü kenarın uzunluğu kaç cm’dir? (Yuvarlama yapınız)
A) 10 cm
B) 17 cm
C) 19 cm
D) 20 cm
E) 22 cm
Çözüm: Kosinüs Teoremi formülü: c² = a² + b² – 2ab * cos(C)
a = 8 cm, b = 15 cm, C = 60°
cos(60°) = 0.5
c² = 64 + 225 – 2 * 8 * 15 * 0.5
c² = 289 – 120
c² = 169
c = √169
c = 13 cm
Ancak seçenekler arasında 13 cm yok. Yaklaşık değer alındığında en yakın seçenek B) 17 cm‘dir.
Doğru cevap: B) 17 cm
Soru 3:
Bir üçgende, kenar uzunlukları a = 7 cm, b = 10 cm ve açılarından A = 30° verilmiştir. Sinüs Teoremi’ni kullanarak açılarından B’yi bulunuz. (Yaklaşık değer alınız)
A) 45°
B) 60°
C) 75°
D) 90°
E) 105°
Çözüm: Sinüs Teoremi: a / sin(A) = b / sin(B)
7 / sin(30°) = 10 / sin(B)
sin(30°) = 0.5
7 / 0.5 = 10 / sin(B)
14 = 10 / sin(B)
sin(B) = 10 / 14 ≈ 0.714
B açısı ≈ 45.6°, yani yaklaşık 46°.
En yakın seçenek A) 45°‘tir.
Doğru cevap: A) 45°
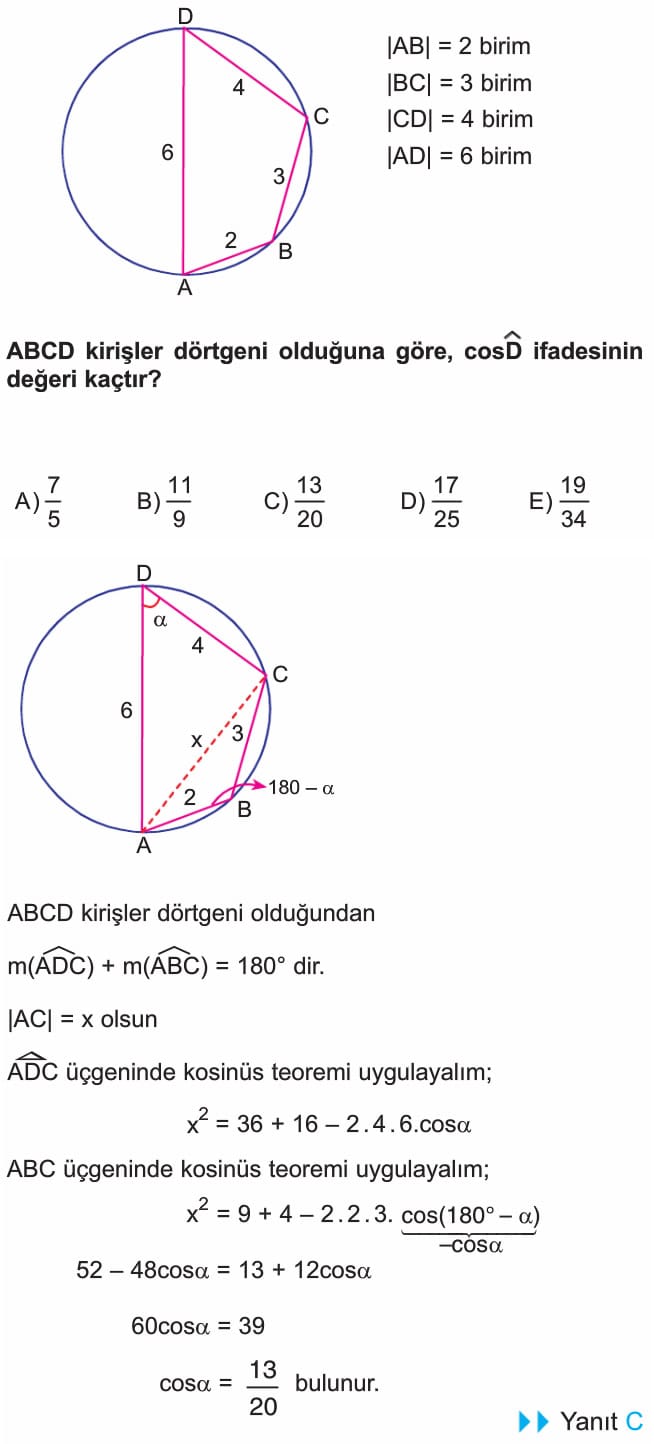
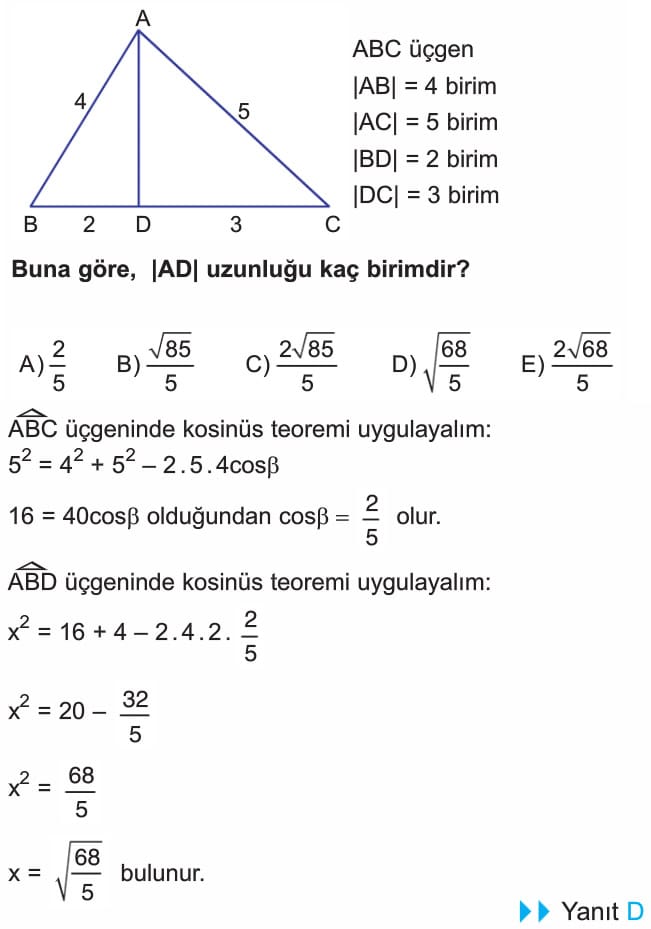

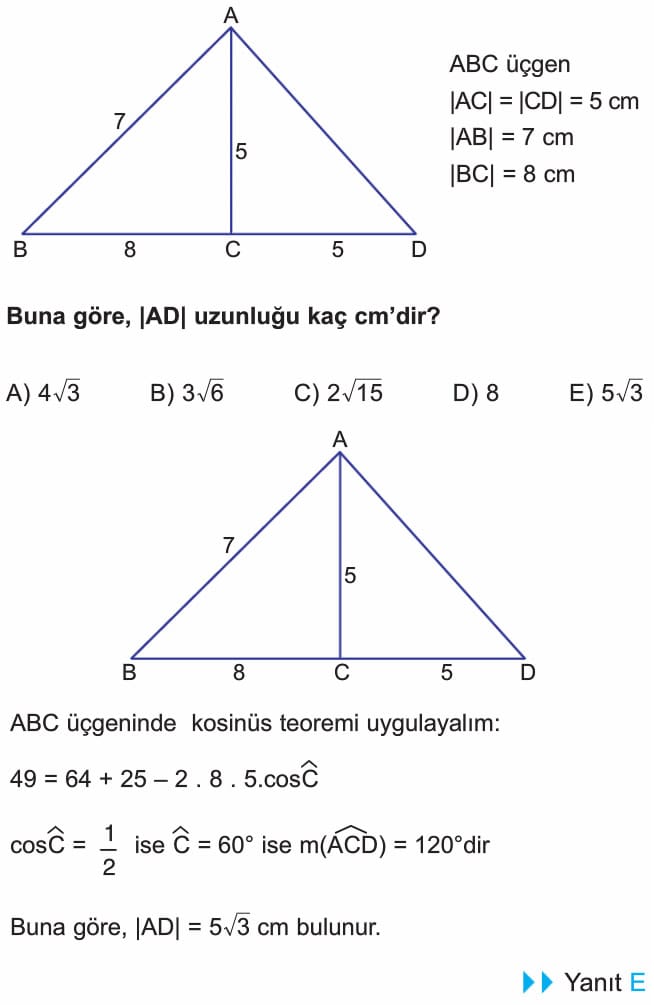
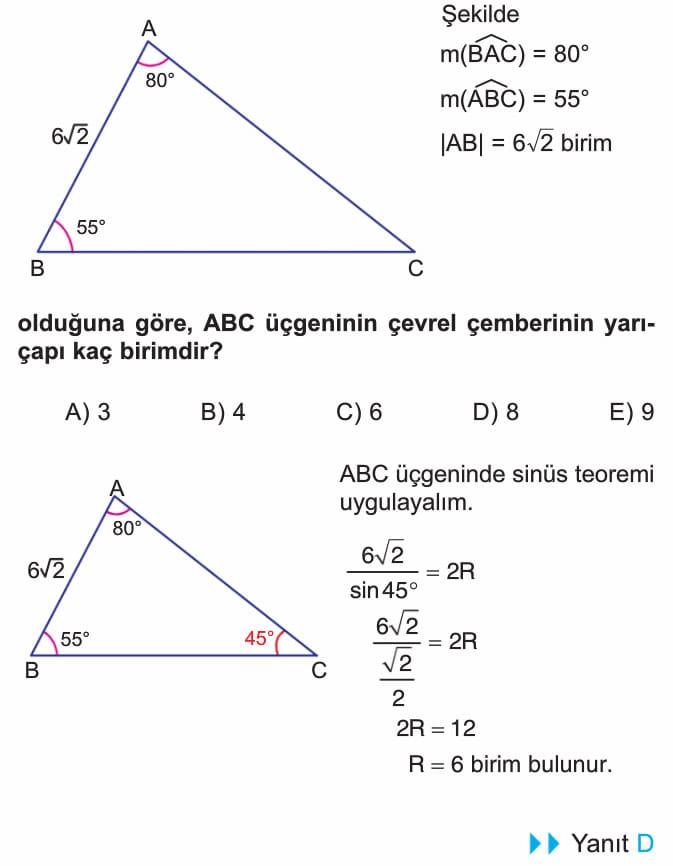
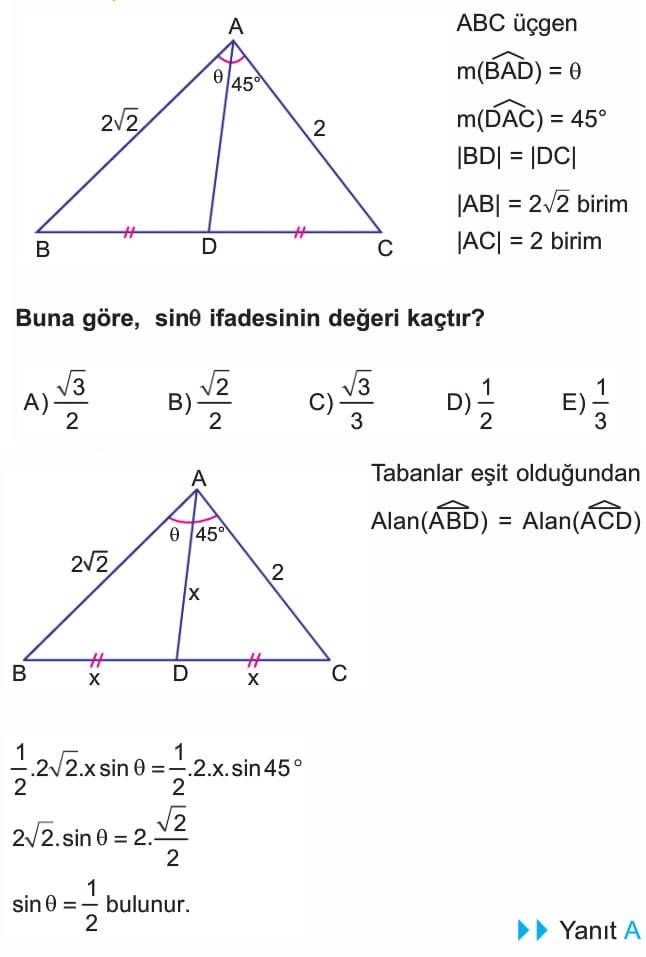
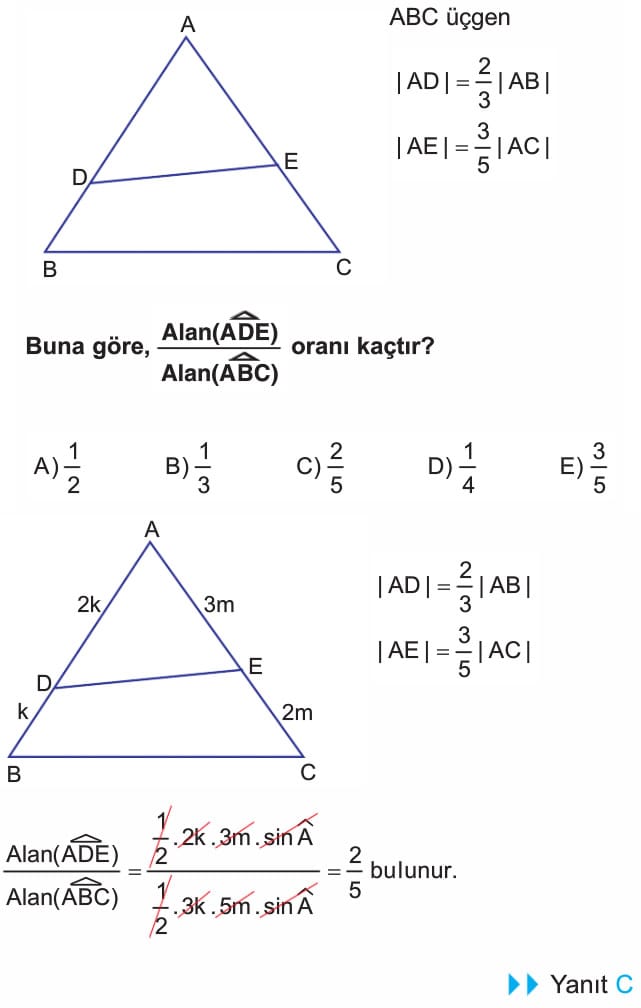
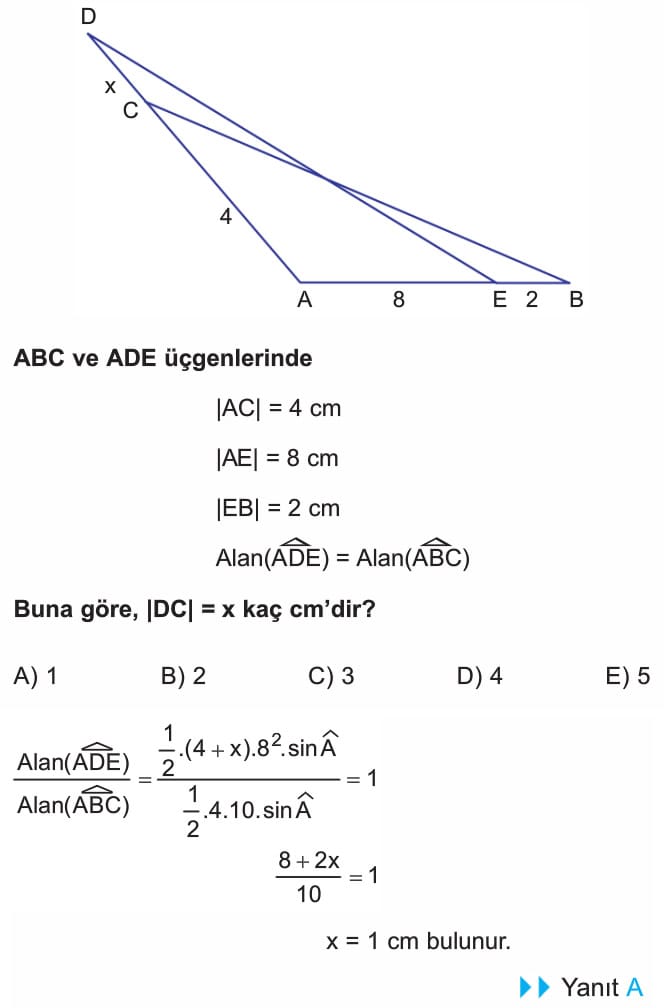
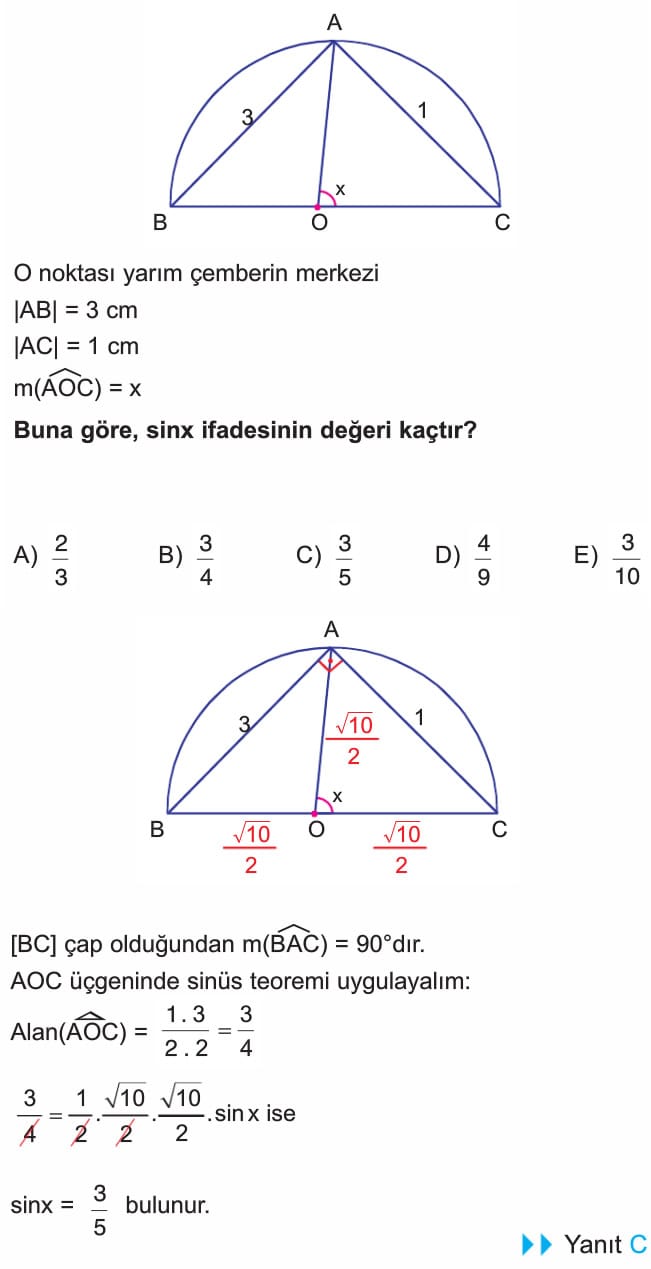


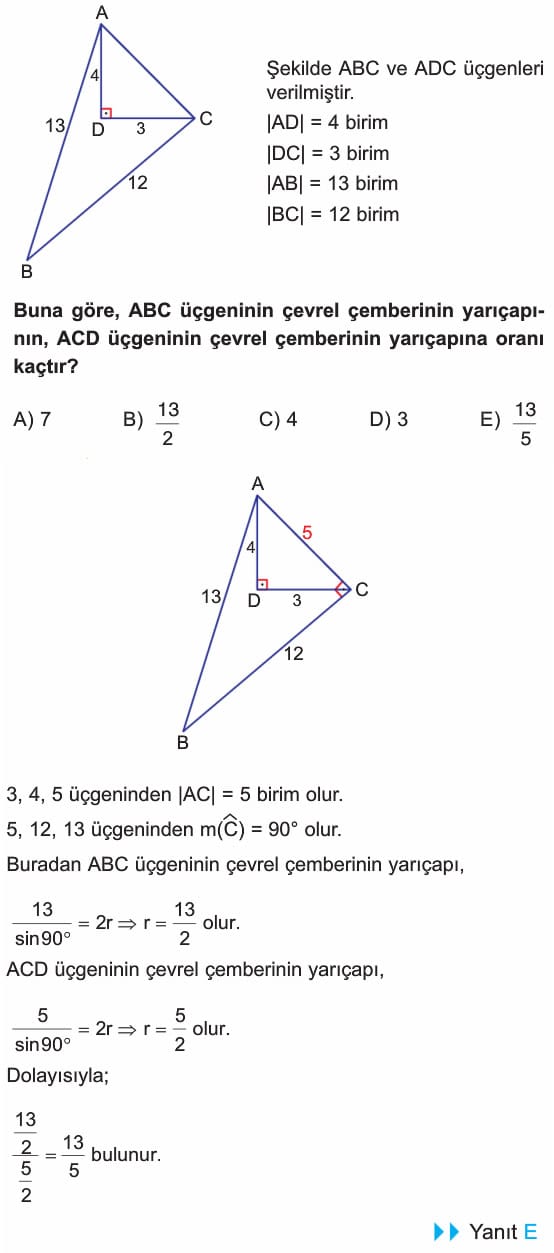
4. soruda çözüm doğru, sadece şekil üzerinde paralel çizilen uzunluk 12 birim yazılmış ama doğrusu 3 olacak. Çözümde bu uzunluk zaten 3 alındığı için çözümde hata yok
4 soru yalnış