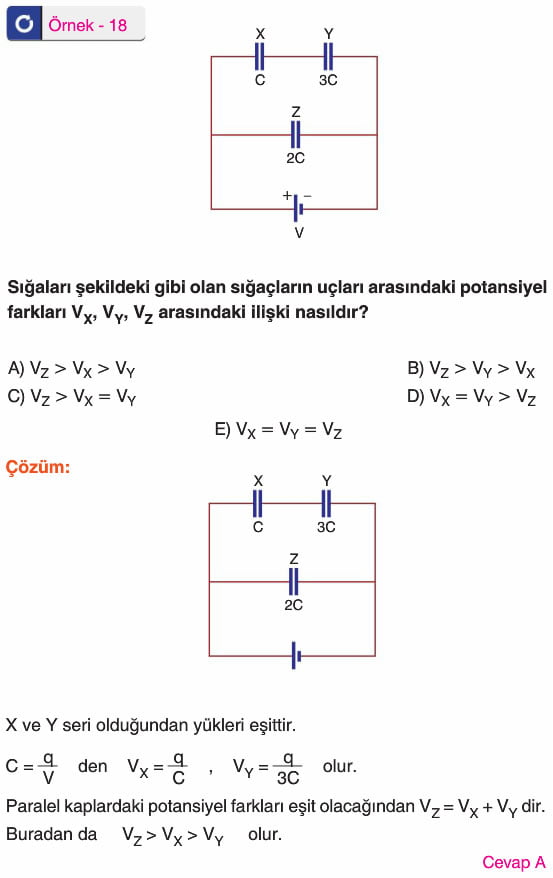
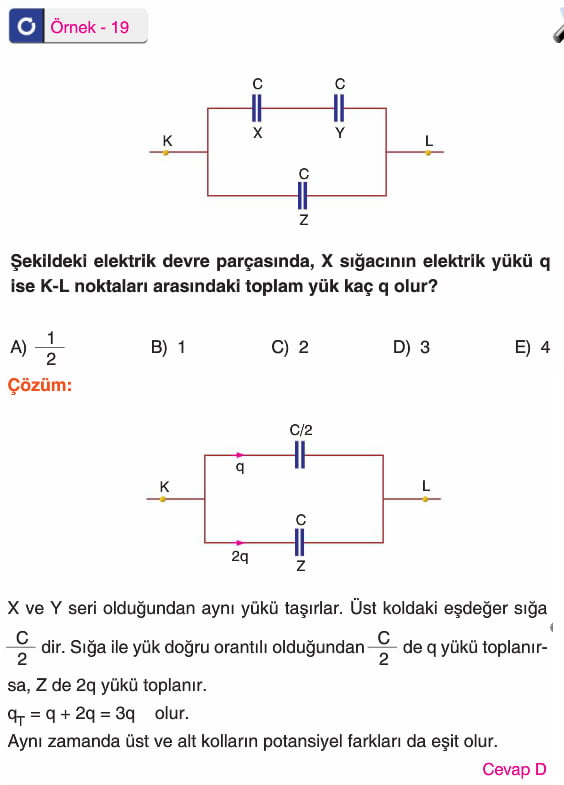
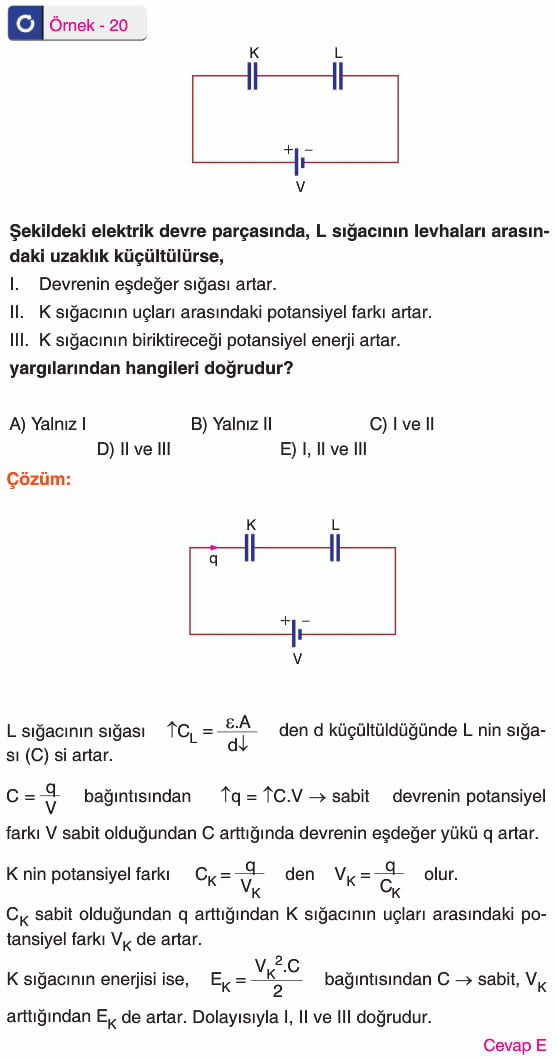
Kondansatörler (Sığaçlar) 11. Sınıf Fizik
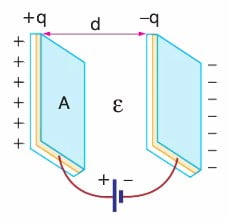
Aralarında yalıtkan bir ortam bulunan iki iletken levhadan oluşan ve elektrik yükü depolamaya yarayan sistemlere kondansatör denir. Kondansatörlerin iletken levhalarına armatür denir. Armatürleri düzlem levhalar şeklinde olan kondansatörler, yüzey alanları A olan iki armatür arasındaki uzaklık d olacak şekilde yan yana getirilip bir üretecin iki kutbuna bağlanması ile elde edilir.
Düzlem kondansatörün sığası C = ε. A/d
A: Levhaların yüzey alanı
d: Levhalar arasındaki uzaklık
ε: Yalıtkan ortamın dielektrik sabiti

Not: Eğer levhaların yüzey alanı eşit değil ise sığa bulunurken küçük levhanın alanı dikkate alınır. Levhalar eşit yüklü olup zıt işaretlidirler.

Sığacın Yükü ve Potansiyeli
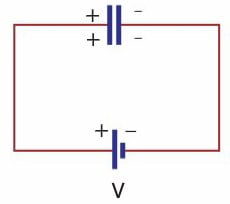
Kondansatörü bir üretecin kutuplarına bağladığımızda onu şekilde gösterildiği gibi yüklemiş oluruz. Üretecin pozitif kut- buna bağlanan levha +q yükünü kazanırsa, negatif kutbuna bağlanan levha -q yükünü kazanır. Sonuç olarak kondansatör q yüküyle yüklenmiş olur. Levhalardaki yük miktarı kondansatörün sığasına ve üretecin potansiyeline bağlıdır. q = C.V
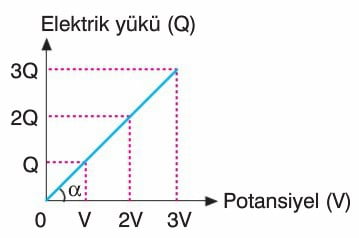
Kondansatörün üzerindeki yükün potansiyeline bağlı değişim grafiği şekildeki gibidir. Bu grafiğin eğimi, kondansatörün sığasını verir.
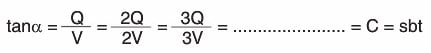
Kondansatörün sığası yukarıda gösterildiği gibi sabittir. Yani üzerindeki yüke ya da gerilime bağlı değildir.
Not: Kondansatörün yükü denilince, levhalardan yalnız birinin yükü, potansiyeli denilince iki levha arasındaki potansiyel farkı anlaşılır.
Sığacın Enerjisi

Sığası C olan bir kondansatörü üretece bağlayarak V potansiyel farkı oluşturursak, kondansatörü Q elektrik yüküyle yüklemiş oluruz. Yükü ve potansiyeli artan kondansatörde Elektriksel Potansiyel enerjisi birikir. Böylece kondansatörü yüklemek için üretecin harcadığı enerji, enerjinin korunumu ilkesine göre kondansatörde depolanmış olur. Kondansatörün yükünün potansiyeline bağlı grafiği şekildeki gibi olur.

Sığaçların Bağlanması
İhtiyaç duyulan değerdeki sığaya sahip tek bir kondansatörü her zaman bulmak mümkün değildir. Böyle durumlarda birden fazla kondansatör seri veya paralel bağlanabilir.
Seri Bağlama
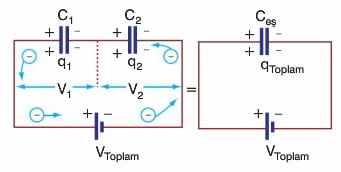
Kondansatörlerin uç uca eklenmesiyle elde edilen bağlama şeklidir. Üretecin verdiği elektronlar (-) kutba bağlı C2 kondansatörünün levhasında birikirler, etki ile elektriklenme yoluyla diğer levha ve kondansatörler de aynı miktarda elektrik yüküyle yüklenirler. Bu nedenle seri bağlı kondansatörlerin yükleri birbirine eşittir. Seri bağlı kondansatörlerin özellikleri şunlardır:


Paralel Bağlama
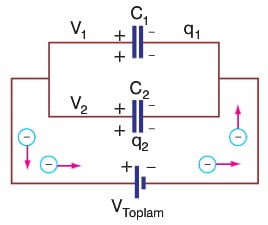
Birden fazla sığacın birer levhaları üretecin bir kutbuna, diğer levhaları da öteki kutbuna bağlanırsa, kondansatörler paralel bağlanmış olur. Üretecin verdiği elektronlar ortak uca geldiklerinde ikiye ayrılarak C1 ve C2 kondansatörlerinin levhalarında birikirler. Daha sonra diğer levhanın elektronlarını iterler. Böylece sistem yüklenmiş olur.

Not: Paralel bağlı kondansatör sisteminde, potansiyel farkları eşit olduğundan q = C.V bağıntısına göre, sığası büyük olan kondansatörün yükü de büyük olur.
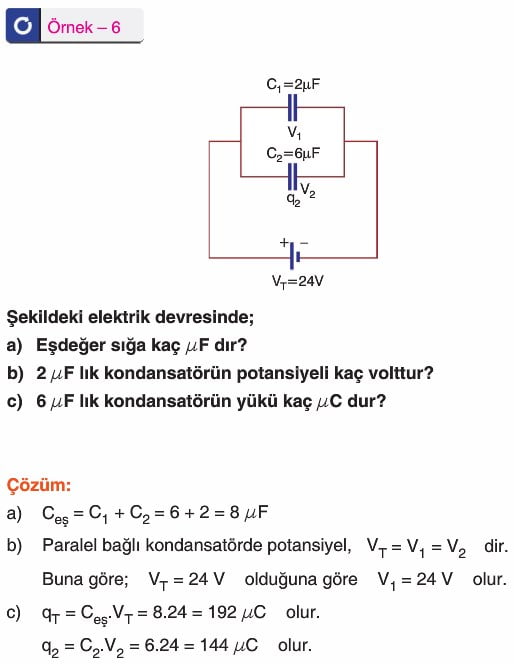
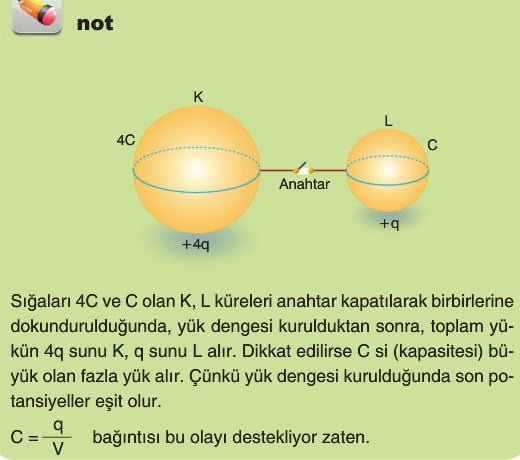
Yüklü İki Sığacın Bağlanması
Yüklü iki kondansatör birbirine iki türlü bağlanabilir.
1. Durum: Aynı kutuplar birbirine bağlandığında (paralel bağlama) kondansatörlerin toplam yükleri korunur. Toplam yük yeni durumda kondansatörler arasında paylaşılır.
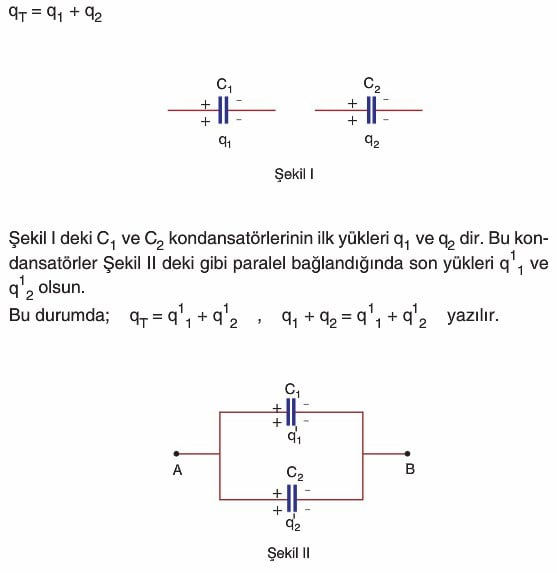
Kondansatörlerin potansiyelleri eşit olacağından, A-B noktaları arasındaki yeni potansiyel farkını V kabul ederek (Ortak Potansiyel)
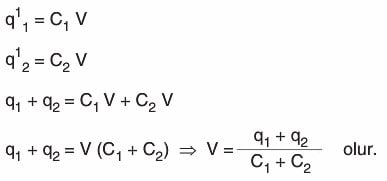
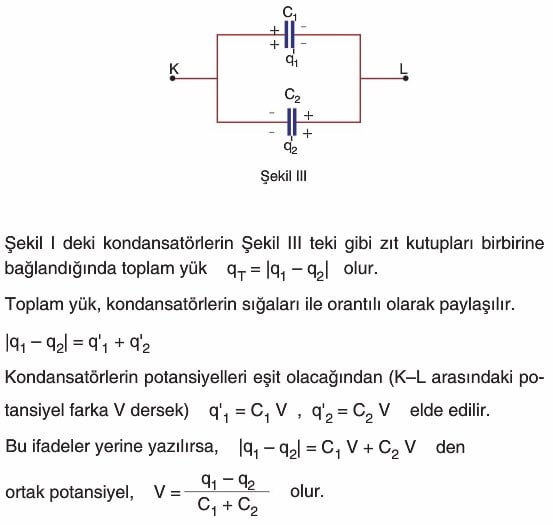
2. Durum
Çözümlü Sorular
Çözümlü Örnek Test Soruları: Kondansatörler (Sığaçlar)
- Bir kondansatörün sığası, aşağıdaki faktörlerden hangisine bağlı değildir?
A) Kondansatör plakaları arasındaki mesafe
B) Kondansatör plakalarının büyüklüğü
C) Kondansatörün şarj ettiği voltaj
D) Kondansatörün içine yerleştirilen dielektrik malzemeÇözüm:
Kondansatörün sığası, plakalar arasındaki mesafe, plakaların büyüklüğü ve dielektrik malzemeye bağlıdır, ancak şarj ettiği voltajla doğrudan ilişkili değildir.
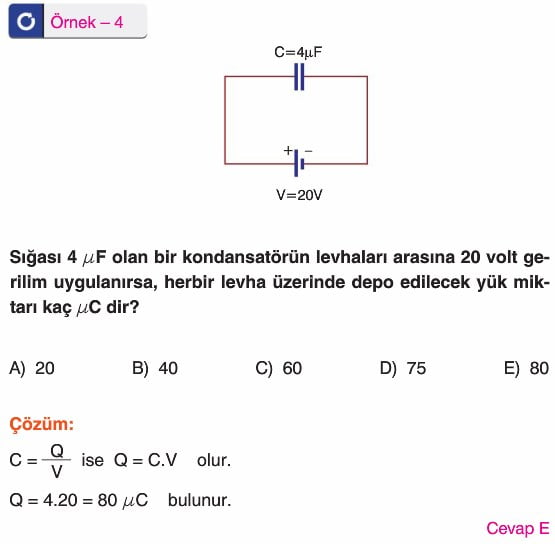
Cevap: C - Bir kondansatörün sığası 10 µF, gerilmesi ise 12 V’dur. Kondansatörün üzerine depolanan enerji nedir?
A) 0,72 J
B) 1,44 J
C) 0,6 J
D) 1,2 JÇözüm:
Kondansatörün depoladığı enerji formülü:
E = 1/2 × C × V²
E = 1/2 × 10 × 10⁻⁶ × 12² = 1/2 × 10 × 10⁻⁶ × 144 = 0,72 × 10⁻³ J = 0,72 J
Cevap: A - Bir kondansatörün sığası 4 µF, gerilmesi 20 V’dur. Kondansatörün depoladığı enerji nedir?
A) 1,6 J
B) 2 J
C) 0,8 J
D) 4 JÇözüm:
E = 1/2 × C × V²
E = 1/2 × 4 × 10⁻⁶ × 20² = 1/2 × 4 × 10⁻⁶ × 400 = 0,8 J
Cevap: C - Kondansatörün sığası 20 µF ve plakalar arasındaki mesafe 1 cm olan bir kondansatörün dielektrik sabiti 2.5’tir. Dielektrik malzeme çıkarıldığında, kondansatörün sığası ne olur?
A) 5 µF
B) 8 µF
C) 10 µF
D) 25 µFÇözüm:
Dielektrik malzeme kondansatörün sığasını artırır. Dielektrik sabiti çıkarıldığında, sığa eski haline döner.
Sığa dielektrik sabiti ile ters orantılıdır.
Cevap: B - Bir kondansatörün kapasitansı 5 µF’dir. Kondansatörün üzerine 15 V gerilim uygulandığında, kondansatörün şarj ettiği yük miktarı nedir?
A) 0,075 C
B) 0,25 C
C) 0,075 µC
D) 0,25 µCÇözüm:
Q = C × V
Q = 5 × 10⁻⁶ × 15 = 75 × 10⁻⁶ C = 0,075 C
Cevap: A

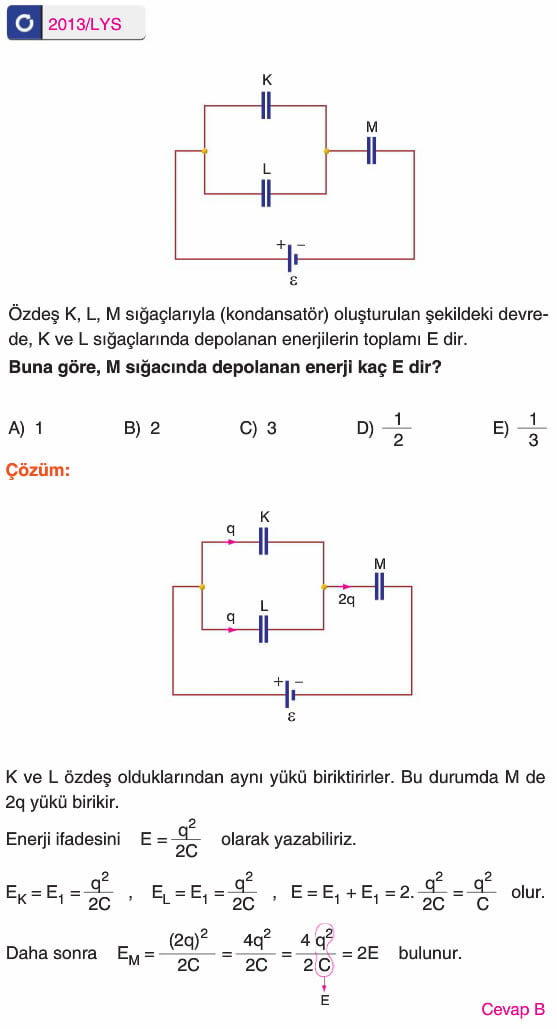
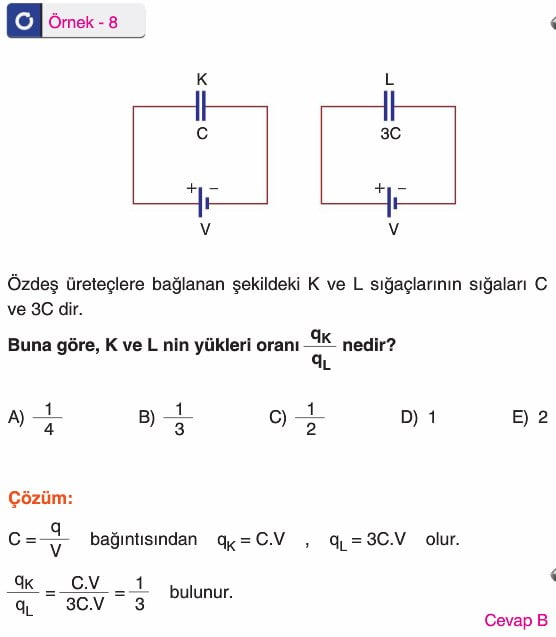


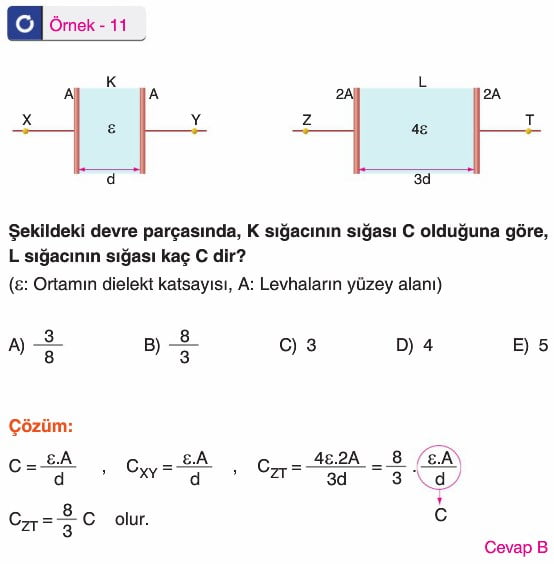

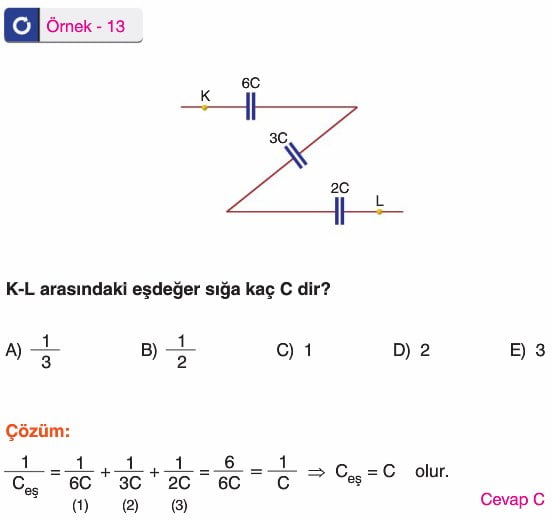
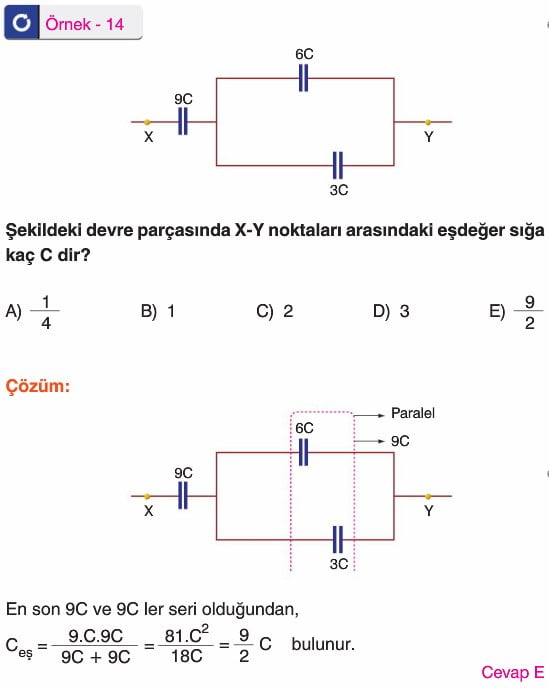
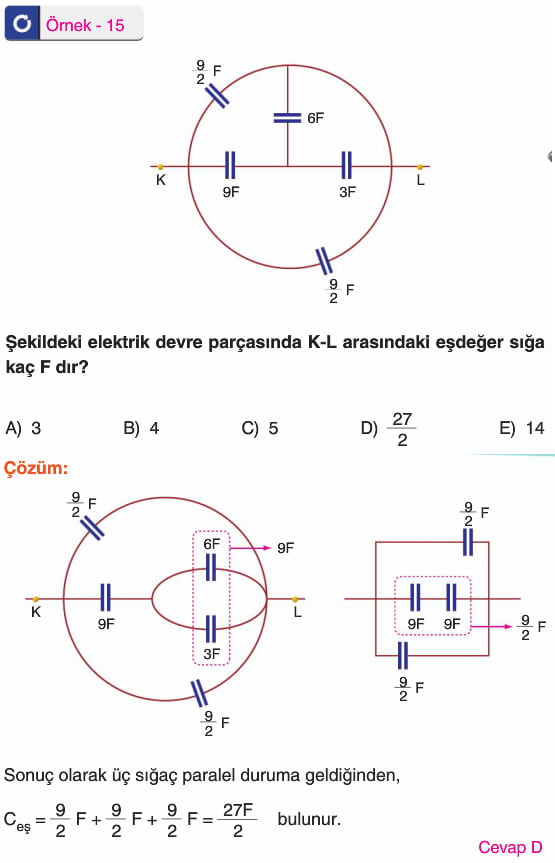
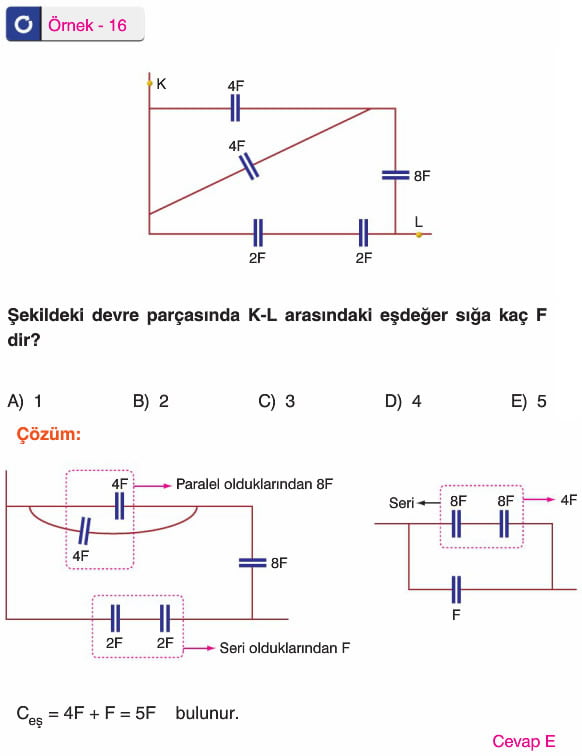
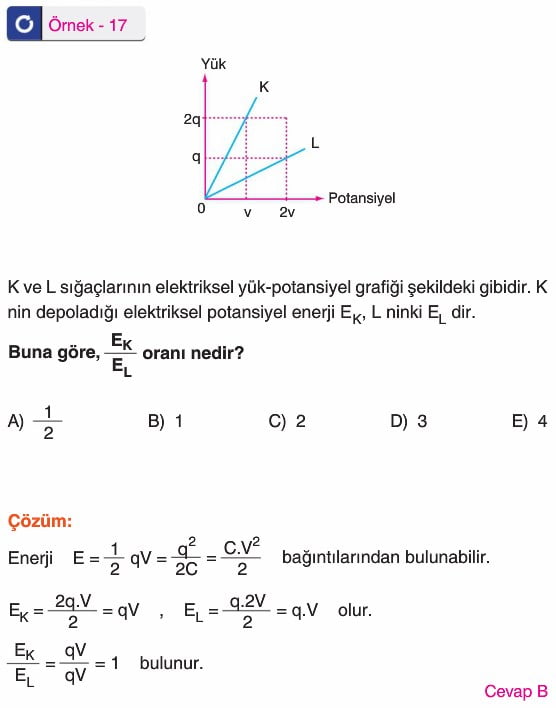
ÇOK GÜZEL OLMUŞ HAZIRLAYANA TEŞEkküR EDERİM