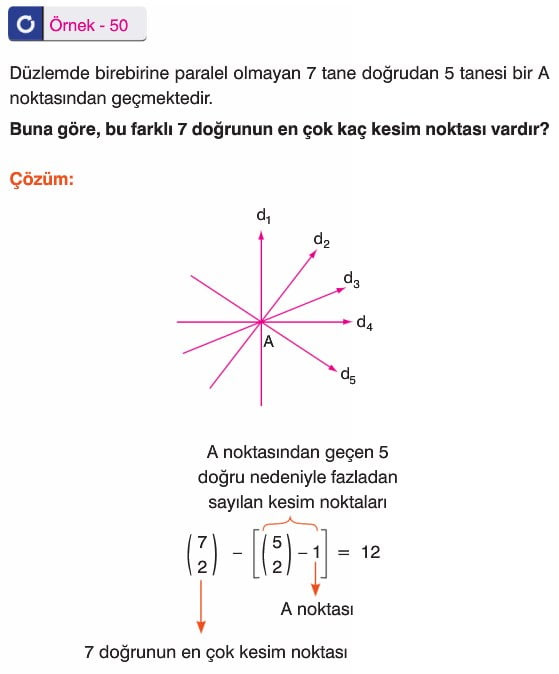
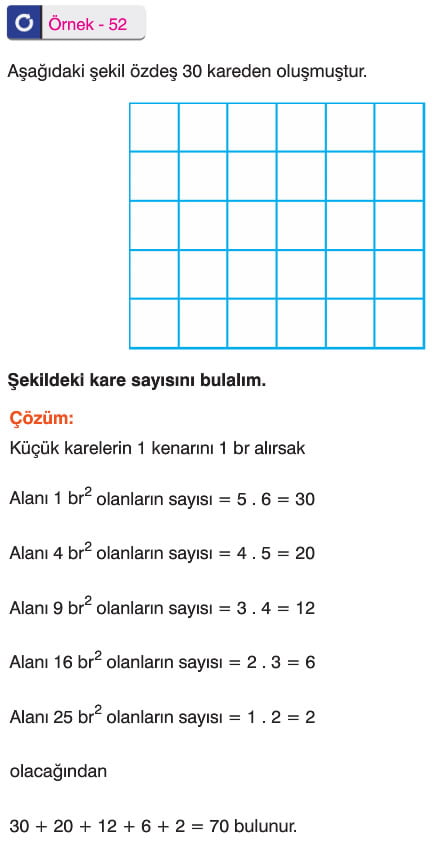
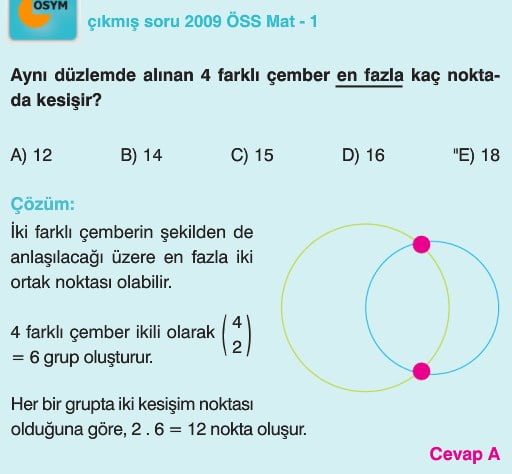
Kombinasyon (Seçme) 10. Sınıf Matematik
Bu yazımızda 10. sınıf matematik dersinin Sayma ve Olasılık Ünitesinden Kombinasyon konusunun ders notları yer almaktadır. Konuyu bitirdikten sonra konu ile ilgili online testler çözebilirsiniz.
10. Sınıf Kombinasyon Testleri
10. Sınıf Permütasyon (Sıralama) Konu Anlatımı
10. Sınıf Kombinasyon (Seçme) Ders Notu
n, r doğal sayı ve n ≥ r olmak üzere, n elemanlı bir kümenin r elemanlı alt kümelerinden her birine n in r li bir kombinasyonu (grubu) denir. n in r li kombinasyonlarının sayısı:

Kombinasyonun Özellikleri

Sonraki Konu: Pascal Üçgeni ve Binom Açılımı
Kombinasyon Soruları ve Çözümleri
1. ÜNİTE: SAYMA VE OLASILIK
A. Sıralama ve Seçme
- Sayma Yöntemleri
- Faktöriyel
- Permütasyon
- Tekrarlı Permütasyon
- Kombinasyon
- Pascal Üçgeni ve Binom Açılımı
B. Basit Olayların Olasılıkları
Kombinasyon, bir kümedeki nesnelerden belirli bir sayıda nesnenin seçilmesini ifade eden bir sayma yöntemidir. Kombinasyonun en temel özelliği, seçilen nesnelerin sırasının önemli olmamasıdır. Yani, hangi nesnenin önce veya sonra seçildiği fark etmez. Bu, permütasyon ile kombinasyon arasındaki temel farktır. Permütasyonda sıralama önemliyken, kombinasyonda sadece elemanların seçimi önemlidir.
Kombinasyonun Kullanım Alanları
Kombinasyon birçok farklı alanda kullanılan bir sayma yöntemidir. Özellikle şu durumlarda kombinasyon kullanılır:
- Olasılık: Bir gruptan elemanların sırasız şekilde seçilmesi gereken olasılık problemlerinde kombinasyon sıkça kullanılır.
- Gruplama: Belirli bir grubu oluşturan elemanların seçilmesinde kullanılır.
- Matematiksel analiz: Sıralamanın önemsiz olduğu matematiksel problemleri çözmede yardımcı olur.
- Bilgisayar bilimleri: Veri kümelerindeki belirli elemanların seçilmesi ve grupların oluşturulması için kombinasyon kullanılır.
Kombinasyon ile Permütasyon Arasındaki Fark
Kombinasyon ve permütasyon arasında temel bir fark vardır: permütasyonda sıralama önemliyken, kombinasyonda sıralama önemsizdir. Bu nedenle, kombinasyon formülünde sıralamayı dikkate alan bir bölme işlemi yapılır. Aynı elemanlar farklı sırada seçildiğinde permütasyon, sırasız seçimde ise kombinasyon kullanılır.
Örnek: 5 kişilik bir gruptan 2 kişi seçmek ve sıralamak permütasyondur. Ancak sadece 2 kişiyi seçmek kombinasyondur.
Kombinasyonun Uygulama Alanları
Kombinasyon, olasılık teorisi, istatistik, bilgisayar bilimleri ve mühendislik gibi birçok alanda geniş kullanım alanına sahiptir. Özellikle seçim, gruplama ve kombinatorik problemlerde sıklıkla karşımıza çıkar. Gerçek hayatta kombinasyon, aşağıdaki gibi durumlarda kullanılabilir:
- Bir basketbol takımının belirli sayıda oyuncusunun sırasız olarak seçilmesi.
- Bir yarışmadaki katılımcıların bir grup halinde rastgele seçilmesi.
- Bir sınavda doğru yanıtlanması gereken soruların seçimi.
Çözümlü Örnek Test Soruları
Soru 1:
Bir grup içinde 6 kişi arasından 2 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 12
B) 15
C) 10
D) 8
E) 6
Çözüm:
6 kişi arasından 2 kişi seçme işlemi C(6, 2) ile ifade edilir:
C(6, 2) = 6! / (2! * (6 – 2)!) = 6! / (2! * 4!) = 15
Doğru Cevap: B
Soru 2:
8 kişilik bir gruptan 3 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 24
B) 56
C) 35
D) 40
E) 28
Çözüm:
8 kişi arasından 3 kişi seçme işlemi C(8, 3) ile ifade edilir:
C(8, 3) = 8! / (3! * (8 – 3)!) = 56
Doğru Cevap: B
Soru 3:
10 kişilik bir gruptan 4 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 100
B) 120
C) 210
D) 252
E) 45
Çözüm:
10 kişi arasından 4 kişi seçme işlemi C(10, 4) ile ifade edilir:
C(10, 4) = 10! / (4! * (10 – 4)!) = 210
Doğru Cevap: C
Soru 4:
7 kişilik bir gruptan 5 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 21
B) 42
C) 35
D) 56
E) 28
Çözüm:
7 kişi arasından 5 kişi seçme işlemi C(7, 5) ile ifade edilir:
C(7, 5) = 7! / (5! * (7 – 5)!) = 21
Doğru Cevap: A
Soru 5:
Bir sınıfta 9 öğrenci arasından 2 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 72
B) 36
C) 45
D) 15
E) 20
Çözüm:
9 kişi arasından 2 kişi seçme işlemi C(9, 2) ile ifade edilir:
C(9, 2) = 9! / (2! * (9 – 2)!) = 36
Doğru Cevap: B
Soru 6:
5 kişilik bir ekipten 3 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 5
B) 6
C) 7
D) 8
E) 10
Çözüm:
5 kişi arasından 3 kişi seçme işlemi C(5, 3) ile ifade edilir:
C(5, 3) = 5! / (3! * (5 – 3)!) = 10
Doğru Cevap: E
Soru 7:
12 kişilik bir gruptan 6 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 924
B) 1001
C) 990
D) 880
E) 760
Çözüm:
12 kişi arasından 6 kişi seçme işlemi C(12, 6) ile ifade edilir:
C(12, 6) = 12! / (6! * (12 – 6)!) = 924
Doğru Cevap: A
Soru 8:
15 kişilik bir gruptan 4 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 1235
B) 1300
C) 1365
D) 1400
E) 1500
Çözüm:
15 kişi arasından 4 kişi seçme işlemi C(15, 4) ile ifade edilir:
C(15, 4) = 15! / (4! * (15 – 4)!) = 1365
Doğru Cevap: C
Soru 9:
10 kişilik bir ekipten 5 kişi seçilecektir. Kaç farklı seçim yapılabilir?
A) 250
B) 300
C) 252
D) 210
E) 280
Çözüm:
10 kişi arasından 5 kişi seçme işlemi C(10, 5) ile ifade edilir:
C(10, 5) = 10! / (5! * (10 – 5)!) = 252
Doğru Cevap: C
Soru 10:
6 kişilik bir gruptan tüm grup seçilirse kaç farklı seçim yapılabilir?
A) 1
B) 2
C) 3
D) 4
E) 6
Çözüm:
Tüm gruptan seçim yapıldığında yalnızca bir seçim olur. Yani C(6, 6) = 1’dir.
Doğru Cevap: A