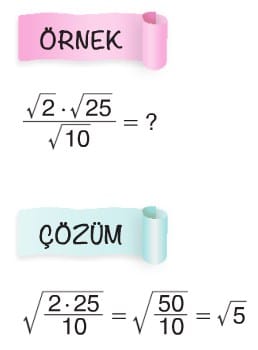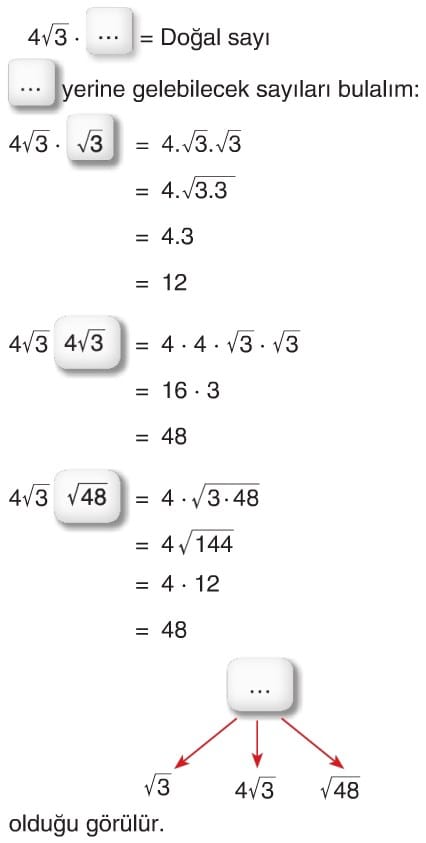Köklü İfadeler 8. Sınıf
Tam Kare Sayılar
- Verilen bir sayının, hangi sayının karesi olduğunu bulma işlemine, karekök alma işlemi denir.
- Karekök ” √ ” sembolü ile gösterilir. √5, karekök beş olarak okunur.
- Bir sayının karesi negatif olamayacağından kökün içerisinde negatif sayı bulunmaz.
- Bir tam sayının karesi olan, diğer bir ifadeyle karekökleri tam sayı olan 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, gibi doğal sayılara tam kare sayılar denir.

Örnek Soru: Aşağıdaki sayılardan hangisi tam kare değildir?
A) 36 B) 64 C) 80 D) 169
Çözüm: 36 = 6 . 6 = 62 olduğundan bir tam kare sayıdır.
64 = 8.8 = 82 olduğundan bir tam kare sayıdır.
80 herhangi bir sayının karesi olmadığından tam kare sayı değildir.
169 = 13 . 13 =132 olduğundan bir tam kare sayıdır. Yanıt C
Tamkare Sayının Karekökü
Örnek Soru: 139 tane bilyeye en az kaç tane daha bilye eklenirse toplam bilye sayısının bir tam kare sayı olacağını bulalım.
Çözüm: 139’dan büyük en küçük tam kare sayı 144 olacağından 144 – 139 = 5 tane bilye eklenirse toplam bilye sayısı, tam kare sayı olur.
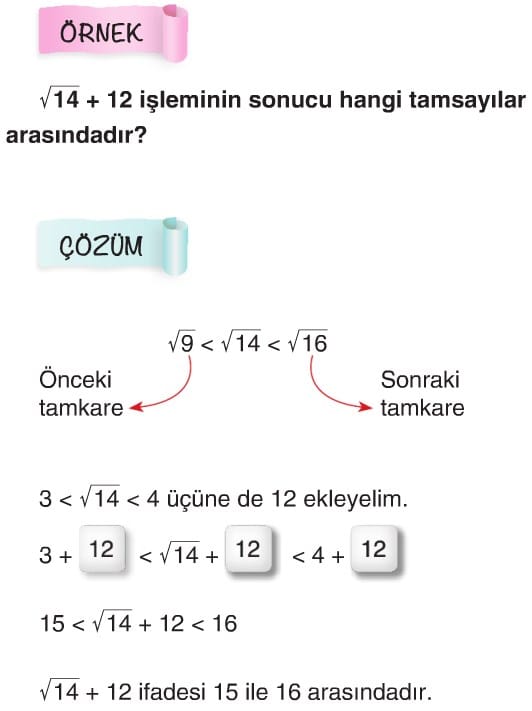
Karekök Değerinin Tahmini
Tam kare olmayan bir sayının hangi tam sayılar arasında olduğunu tahmin ederken aşağıdaki adımlar izlenir.
1.Adım: Tam kare olmayan sayının hangi iki ardışık tam kare sayının arasında olduğu tespit edilir.
2. Adım: 1. adımda yazılan sayıların hepsinin karekökü alınır.
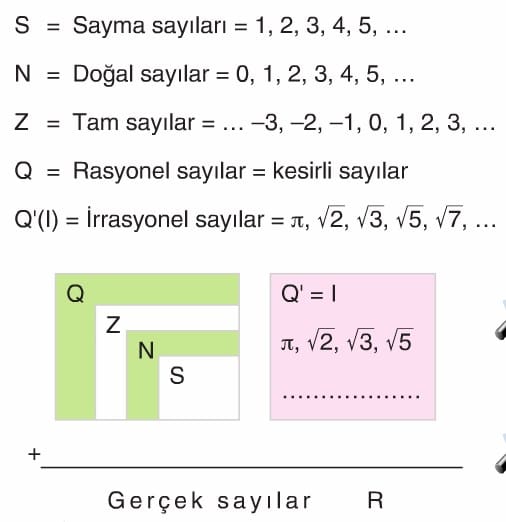
Sayı Sistemleri
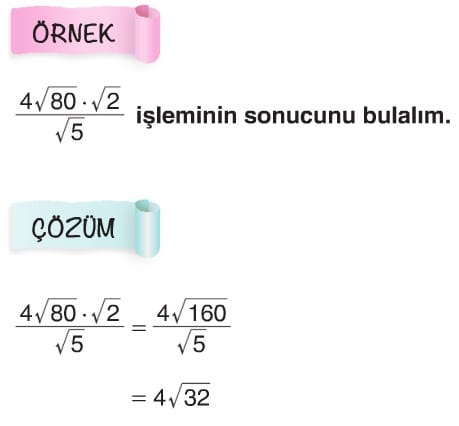
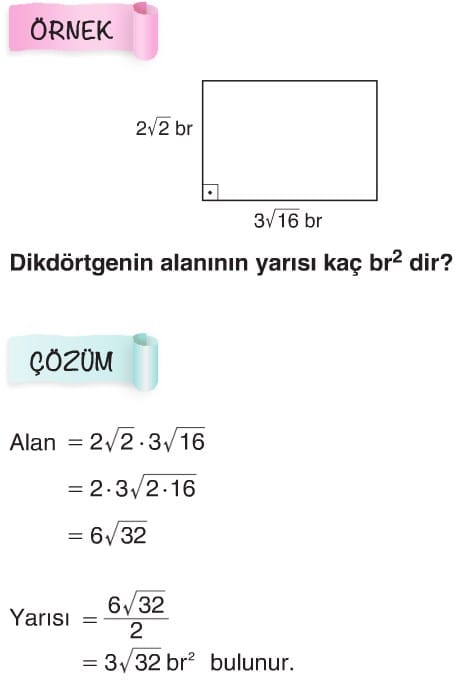
Köklü Sayılarda Çarpma ve Bölme
Sayıları a.√b şeklinde yazalım
İrrasyonel . İrrasyonel = Doğal Sayı
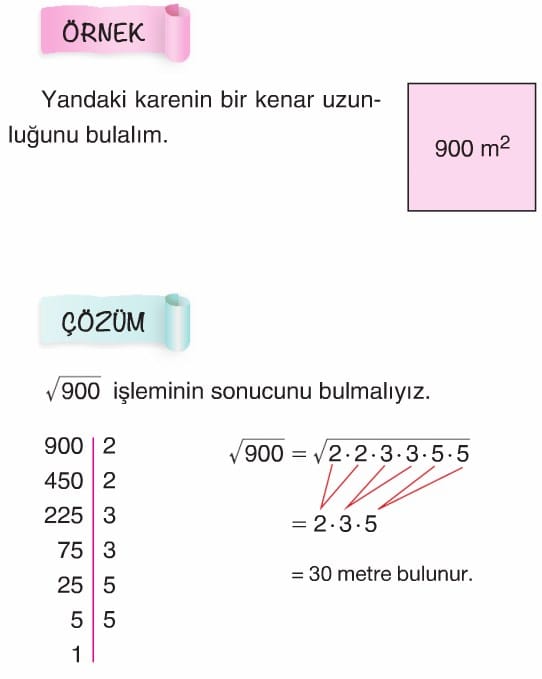
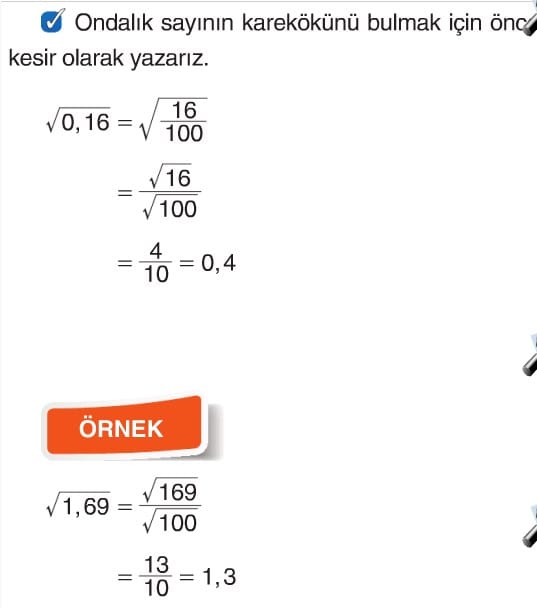
Ondalık Sayıların Karekökleri
Köklü Sayılarda Toplama – Çıkarma
KAREKÖKLÜ İFADELERDE SIRALAMA
- Kareköklü ve kareköklü olmayan sayıları sıralarken
- Kareköklü olmayan sayılar kareköklü biçimde yazılır.
- Karekök dışındaki katsayılar içeri alınır.
- Pozitif işaretli kareköklü sayılarda kök içi büyük olan daha büyük olur.
- Negatif işaretli kareköklü sayılarda kök içi küçük olan daha büyük olur.
Köklü Sayılar konu anlatımı 8.sınıf Kareköklü İfadeler Ders Notu Çözümlü Sorular Lgs
Örnek: Yüzler basamağı iki olan kaç tane üç basamaklı tamkare sayı vardır?
Çözüm: On beş çarpı on beş eşittir 225, on altı çarpı on altı eşittir 256 ve on yedi çarpı on yedi eşittir 289 olduğundan 3 tane vardır.
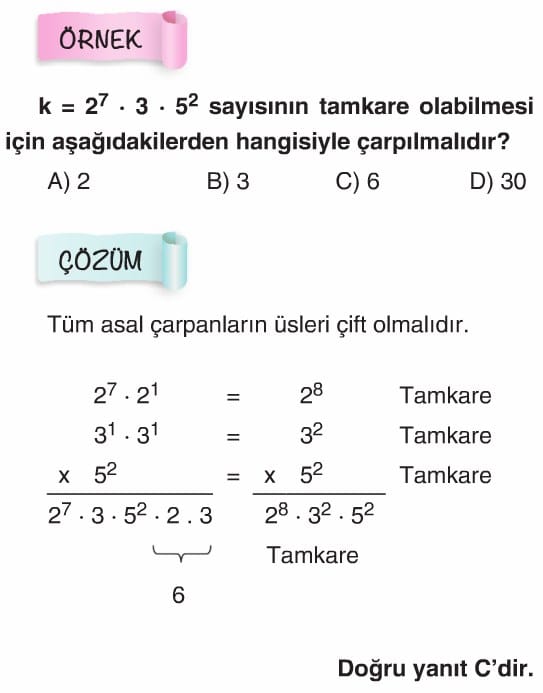
Örnek: k eşittir iki üzeri yedi çarpı üç çarpı beş üzeri iki sayısının tamkare olabilmesi için aşağıdakilerden hangisiyle çarpılmalıdır.
Çözüm: Tamkare sayıların tüm çarpanlarının kuvvetleri çift sayıdır. k sayısında iki ve üç sayılarının kuvvetleri tek sayıdır. k sayısının 3 ve 2 ile çarparsak tamkare sayı olur. Yani k nın 6 ile çarpılması gerekmektedir.
Otuz altı santimetre kare alana sah,p b,r karenin alanının hesaplamak için altı çarpı altı eşittir otuz altı eşitliğini kullanabiliriz. karekök otuz altı eşittir altı. Karenin bir kenar uzunluğu altı santimetredir.
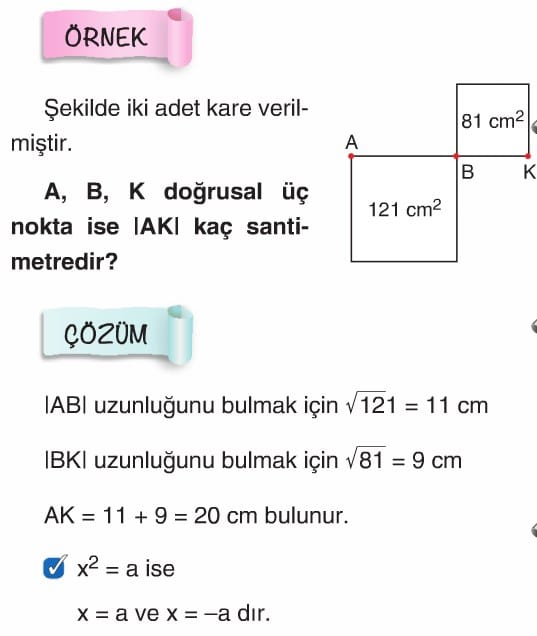
Örnek: Şekilde alanları seksen bir santimetre kare ve yüz yirmi bir santimetre kare olan iki kare verilmiştir. A, B, K doğrusal üç nokta ise AK uzunluğu kaç santimetredir.
Çözüm: AB uzunluğunu bulmak için karekök 121 eşittir 11 santimetre, BK uzunluğunu bulmak için karekök 81 eşittir 9 santimetre, buradan AK uzunluğu 11 artı 9 eşittir 20 santimetre bulunur.
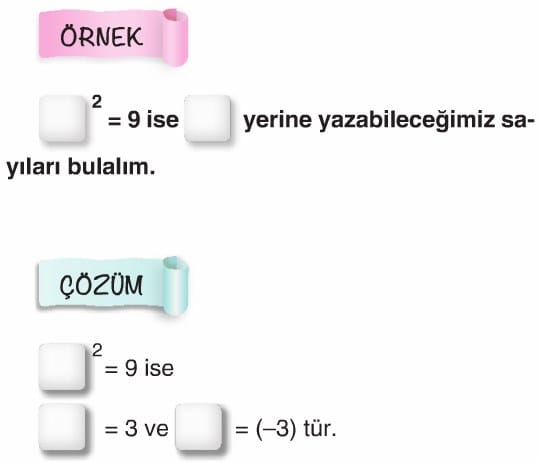
* x kare eşittir a ise x eşittir karekök a veya x eşittir eksi karekök a dır.
Not: karekök dokuz eşittir üç doğru, karekök dokuz eşittir eksi üç yanlıştır.
Karekök içindeki sayı negatif olamaz. karekök eksi eksi dokuz eşittir üç olur. Karekök eksi dokuz olamaz.
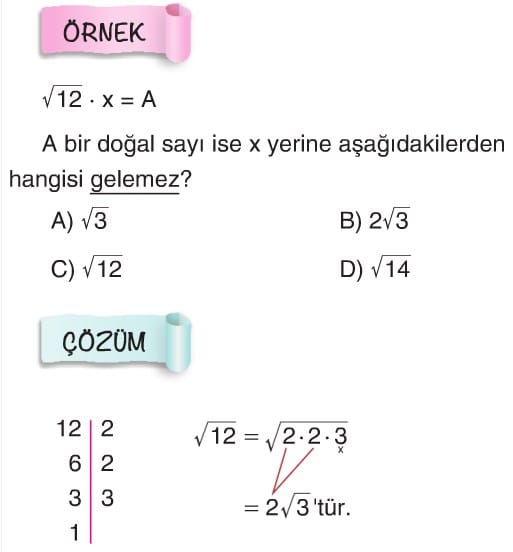
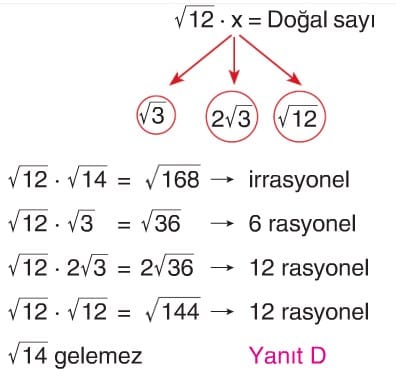
Örnek: kare kök on iki çarpı x eşittir A, A bir doğal sayı ise x yerine gelebilecek en küçük doğal sayı kaçtır.
Çözüm: on iki sayısının asal çarpanları 2 üzeri 2 ve 3 tür. Dolayısıyla A nın doğal sayı olabilmesi için x in en az 3 olması gerekmektedir.
Örnek: Yüzler basamağı iki olan kaç tane üç basamaklı tamkare sayı vardır?
Çözüm: On beş çarpı on beş eşittir 225, on altı çarpı on altı eşittir 256 ve on yedi çarpı on yedi eşittir 289 olduğundan 3 tane vardır.
Örnek: k eşittir iki üzeri yedi çarpı üç çarpı beş üzeri iki sayısının tamkare olabilmesi için aşağıdakilerden hangisiyle çarpılmalıdır.
Çözüm: Tamkare sayıların tüm çarpanlarının kuvvetleri çift sayıdır. k sayısında iki ve üç sayılarının kuvvetleri tek sayıdır. k sayısının 3 ve 2 ile çarparsak tamkare sayı olur. Yani k nın 6 ile çarpılması gerekmektedir.
Otuz altı santimetre kare alana sah,p b,r karenin alanının hesaplamak için altı çarpı altı eşittir otuz altı eşitliğini kullanabiliriz. karekök otuz altı eşittir altı. Karenin bir kenar uzunluğu altı santimetredir.
Örnek: Şekilde alanları seksen bir santimetre kare ve yüz yirmi bir santimetre kare olan iki kare verilmiştir. A, B, K doğrusal üç nokta ise AK uzunluğu kaç santimetredir.
Çözüm: AB uzunluğunu bulmak için karekök 121 eşittir 11 santimetre, BK uzunluğunu bulmak için karekök 81 eşittir 9 santimetre, buradan AK uzunluğu 11 artı 9 eşittir 20 santimetre bulunur.
* x kare eşittir a ise x eşittir karekök a veya x eşittir eksi karekök a dır.
Not: karekök dokuz eşittir üç doğru, karekök dokuz eşittir eksi üç yanlıştır.
Karekök içindeki sayı negatif olamaz. karekök eksi eksi dokuz eşittir üç olur. Karekök eksi dokuz olamaz.
Örnek: kare kök on iki çarpı x eşittir A, A bir doğal sayı ise x yerine gelebilecek en küçük doğal sayı kaçtır.
Çözüm: on iki sayısının asal çarpanları 2 üzeri 2 ve 3 tür. Dolayısıyla A nın doğal sayı olabilmesi için x in en az 3 olması gerekmektedir.












 </a
</a