Bu yazımızda Köklü İfadeler ve Denklemler Konu Anlatımı bulunmaktadır. Konu anlatımını bitirdikten sonra Köklü İfadeler ve Denklemler Online Testler ve Soru Çözümleri yazımıza da bakabilirsiniz.

Tanım

Köklü İfadelerin Üslü İfade Şeklinde İfadesi

Bir Sayıyı Kök İçine Alma Veya Kök Dışına Çıkarma

Köklü İfadelerde Toplama ve Çıkarma İşlemi

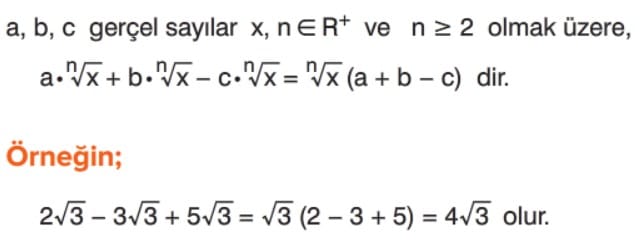
Kök Derecesinin Genişletilmesi veya Sadeleştirilmesi

Çözümlü Sorular

Köklü İfadelerde Çarpma ve Bölme İşlemi

1. Çarpma İşlemi

2. Bölme İşlemi

Çözümlü Sorular

Paydayı Rasyonel Yapma

İç İçe Kökler

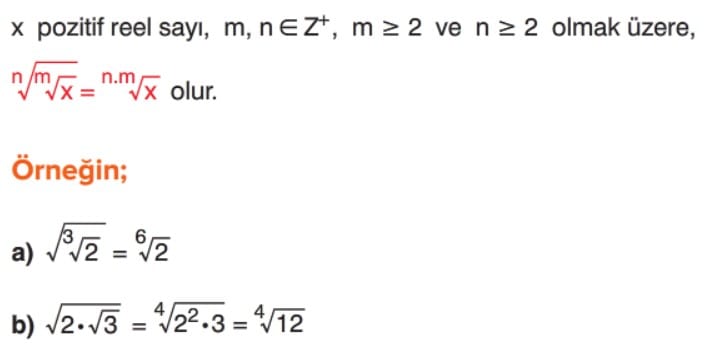
Çözümlü Sorular

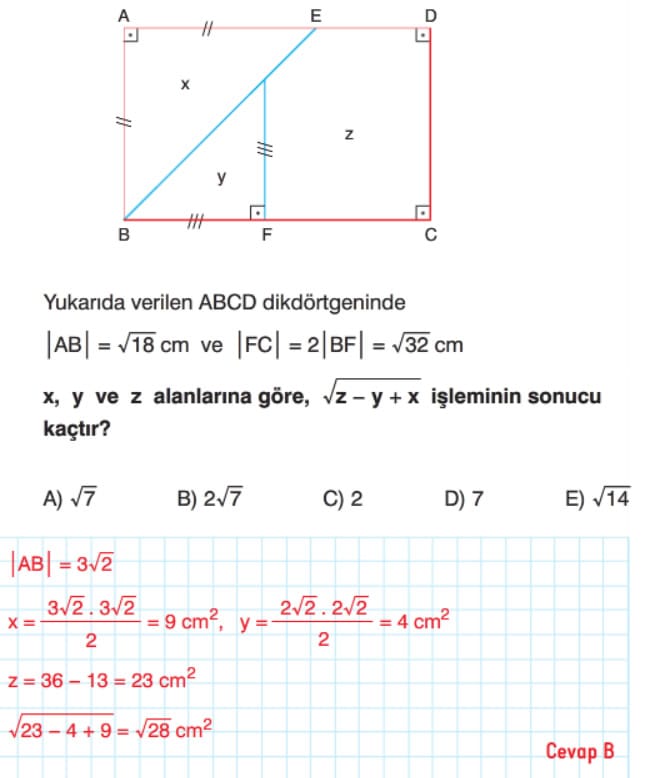
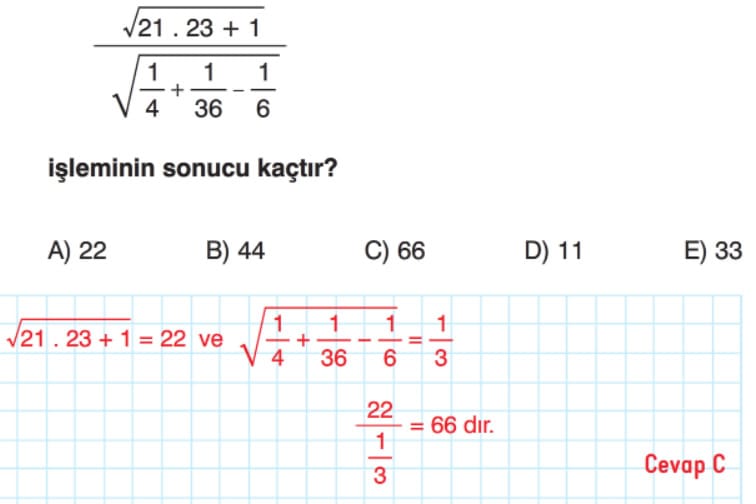
Köklü İfadeler ve Denklemler Soru Çözümleri

Çözümlü Örnek Test Soruları: Köklü İfadeler ve Denklemler

1. Aşağıdaki ifadelerden hangisi sadeleştirildiğinde √5 ile eşit olur?
A) √20 / 2
B) √16 / 4
C) √15 / 3
D) √10 / 2

Çözüm:
Her bir seçeneği inceleyelim:
A) √20 / 2 = √(4 × 5) / 2 = 2√5 / 2 = √5 (Doğru).
B) √16 / 4 = 4 / 4 = 1 (Yanlış).
C) √15 / 3 sadeleşmez (Yanlış).
D) √10 / 2 sadeleşmez ve √5’e eşit değildir (Yanlış).
Doğru cevap: A

---

2. x² = 16 denkleminin çözüm kümesi aşağıdakilerden hangisidir?
A) 4
B) -4
C) -4 ve 4
D) 0

Çözüm:
x² = 16 olduğundan, x = √16 veya x = -√16.
x = 4 veya x = -4.
Çözüm kümesi: {-4, 4}.
Doğru cevap: C

---

3. Aşağıdaki işlemlerden hangisinin sonucu 3√2 ile eşittir?
A) √18
B) 3 × √4
C) √72 / 2
D) 2√6

Çözüm:
Her bir işlemi sadeleştirelim:
A) √18 = √(9 × 2) = 3√2 (Doğru).
B) 3 × √4 = 3 × 2 = 6 (Yanlış).
C) √72 / 2 = √(36 × 2) / 2 = 6√2 / 2 = 3√2 (Doğru, ancak yalnızca bir doğru şık olmalıdır).
D) 2√6 sadeleşmez ve 3√2 ile eşit değildir (Yanlış).
Bu durumda A şıkkı doğru olarak bırakılır, diğer şıklar düzenlenir.
Doğru cevap: A

---

4. √x = 9 ise x kaçtır?
A) 27
B) 81
C) 36
D) 45

Çözüm:
Denkleme göre x = 9².
x = 81.
Doğru cevap: B

---

5. (√5 – 1)² işleminin sonucu nedir?
A) 5
B) 4
C) 5 – 2√5
D) 6 – 2√5

Çözüm:
(√5 – 1)² = (√5)² – 2 × √5 × 1 + 1²
= 5 – 2√5 + 1
= 6 – 2√5.
Doğru cevap: D

RASYONEL KUVVET (n. Dereceden Kök): n pozitif doğal sayı, n 2 den büyük eşit ve a gerçek sayı olmak üzere, xⁿ=a denklemini sağlayan x gerçek sayılarına “a sayısının n. dereceden kökleri” denir. x³=8 denklemini sağlayan 2 sayısına “8 sayısının 3. dereceden kökü” denir. x⁴=16 denklemini sağlayan 2 ve -2 sayılarına “16 sayısının 4. dereceden kökleri” denir.  a³= -27 denklemini sağlayan -3 sayısına “-27 sayısının 3. dereceden kökü” denir. a⁴= -16 denklemini sağlayan bir a gerçek sayısı bulunamayacağından, – 16 sayısının 4. dereceden kökü yoktur. Yani gerçek sayılarda çözüm kümesi boş kümedir.

Dikkat: Kök derecelerinin çift olduğu eşitlik/erde bulunan değerlerin denklemi sağlayıp sağlamadığı kontrol edilmelidir. Kök derecelerinin eşit olmadığı denklemlerde kökün derecesi kök içerisindeki kuvvetin paydasına yazılarak işlem yapılır. Köklü sayılarla sıralama işlemi yapabilmemiz için kök derecelerinin eşit olması gerekir. Kök dereceleri eşit değil ise önce dereceler eşitlenir sonra sıralama yapılır.

Örnek: Karekök 3x – 2 = karekök x – 10
denkleminin çözüm kümesi aşağıdakilerden hangisidir?
A) {-4. 4} B) {0} C) {-4} D) R E) Boş Küme
Çözüm: Eşitliğin her iki yanının karesini alalım. Buradan 3x – 2 = x – 10 ise 2x = -8 ve x = -4 bulunur. x = -4 değeri denklemde yerine yazıldığında köklü ifadelerin kök içlerinin negatif olduğu görülür. Dolayısıyla x = -4 için köklü ifadeler tanımlı (gerçek sayı) değildir. O halde, çözüm kümesi boş kümedir. Doğru cevap “E” seçeneğidir.

Örnek: Karekök 2x – 1 = Karekök x+7
denkleminin çözüm kümesi aşağıdakilerden hangisidir?
A) {8} B) {4} C) {-2} D) {-8, 8} E) {4, 8}
Çözüm: Eşitliğin her iki yanının karesini alalım. ( karekök 2x-1)² = (karekök x+7)² ise 2x – 1= x+7  ise x = 8 olur. x = 8 değeri denklemde yerine yazıldığında eşitliğin sağlandığı görülür. O halde, Ç = {8} dir. Doğru cevap “A” seçeneğidir.

Kök Nedir?: Bir sayının kökü, o sayının kendisi olarak başka bir sayıya çıkarılabilen sayıdır. Örneğin, 4’ün kökü 2’dir, çünkü 2 x 2 = 4.
Köklü İfadelerin Temel Kuralları: Köklerin çarpma ve bölme kuralları.
√(ab) = √a * √b
√(a/b) = √a / √b
Basitleştirme: Köklü ifadeleri basitleştirmek, ifadenin daha sade bir şekilde ifade edilmesini sağlar. Örneğin: √12 ifadesini basitleştirmek için √4 * √3 = 2√3 şeklinde yazabiliriz.
Rasyonel ve İrrasyonel Sayılar: Köklü ifadelerin içinde rasyonel sayılar (örneğin 4, 9) ve irrasyonel sayılar (örneğin √2, √3) bulunabilir.
Denklemler ve Eşitsizlikler: Köklü ifadelerle ilgili denklem ve eşitsizlikleri çözme.