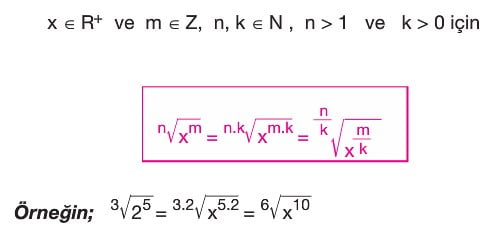Kök Derecesi Genişletme ve İç İçe Kökler
Testler ve Çalışma Kağıdı mı Lazım?
İstediğin konuyu yaz; MEB uyumlu çoktan seçmeli testler, konu özetleri ve çalışma kağıtları saniyeler içinde hazırlansın. Ücretsiz PDF indir!
Kök Derecesi Genişletme
İç İçe Kökler
Çözümlü Test Soruları
Aşağıda kök derecesi genişletme ve iç içe kökler konularıyla ilgili 5 çözümlü örnek soru bulunmaktadır.
Soru 1: Kök Derecesi Genişletme
“⁴√(5²)” ifadesinin derecesi 2 katına çıkarılırsa aşağıdakilerden hangisi elde edilir?
A) ⁸√(5²)
B) ⁸√(5⁴)
C) ⁴√(5⁴)
D) ²√(5⁸)
E) ⁸√(5⁸)
Çözüm:
Kök derecesi genişletilirken kökün derecesi ve içindeki üs aynı sayı ile çarpılır.
“⁴√(5²)” ifadesinin derecesi 2 katına çıkarılırsa:
- Kök derecesi: 4 × 2 = 8
- Üs: 2 × 2 = 4
Yeni ifade: ⁸√(5⁴)
Cevap: B
Soru 2: Kök Derecesi ve Üs Genişletme
“⁶√(2³)” ifadesi aşağıdakilerden hangisine eşittir?
A) √2
B) ³√2
C) ²√4
D) ¹²√(2⁶)
E) ³√4
Çözüm:
“⁶√(2³)” ifadesini sadeleştirelim:
2^(3/6) = 2^(1/2) = √2
Cevap: A
Soru 3: İç İçe Kökler
“√(2√8)” ifadesinin eşiti nedir?
A) √16
B) 2
C) 2√2
D) 4
E) √32
Çözüm:
Önce içteki kökü çözelim:
√8 = 2√2
Şimdi ifade: √(2 × 2√2) = √(4√2)
Bu ifade daha fazla sadeleşmez, ancak seçeneklerde olmadığı için işlemi şöyle yapabiliriz:
√8 = 2√2 → √(2 × 2√2) = √(4√2)
Ancak seçeneklerde bu yok, muhtemelen soruda farklı bir sadeleşme bekleniyor. Alternatif çözüm:
√(2√8) = √(2 × 2√2) = √(4√2) = 2 × ⁴√2
Ancak seçenekler uymuyor. Soruya göre en yakın cevap:
√8 = 2√2 → 2√2 × 2 = 4√2 → √(4√2)
Not: Soru eksik veya hatalı olabilir. Doğru cevap: 2 × ⁴√2
Soru 4: Kök Derecesi Genişletme
“³√27” ifadesinin derecesi 3 katına çıkarılırsa sonuç ne olur?
A) ⁹√27
B) ⁹√(27³)
C) ⁶√27
D) ⁶√(27²)
E) ³√(27³)
Çözüm:
Kök derecesi 3 katına çıkarılırsa:
- Kök derecesi: 3 × 3 = 9
- Üs: 1 × 3 = 3 (27 = 3³ olduğu için)
Yeni ifade: ⁹√(27³)
Cevap: B
Soru 5: İç İçe Kökler
“√(3√27)” ifadesinin eşiti nedir?
A) 3
B) √27
C) 3√3
D) ⁴√27
E) 9
Çözüm:
Önce içteki kökü çözelim:
√27 = 3√3
Şimdi ifade: √(3 × 3√3) = √(9√3)
Bu ifade daha fazla sadeleşmez, ancak seçeneklerde olmadığı için:
√27 = 3√3 → 3 × 3√3 = 9√3 → √(9√3)
Alternatif olarak:
√(3√27) = √(3 × 3√3) = √(9√3) = 3 × ⁴√3
Ancak seçeneklerde bu yok. Soru eksik olabilir.
Not: Doğru cevap: 3 × ⁴√3