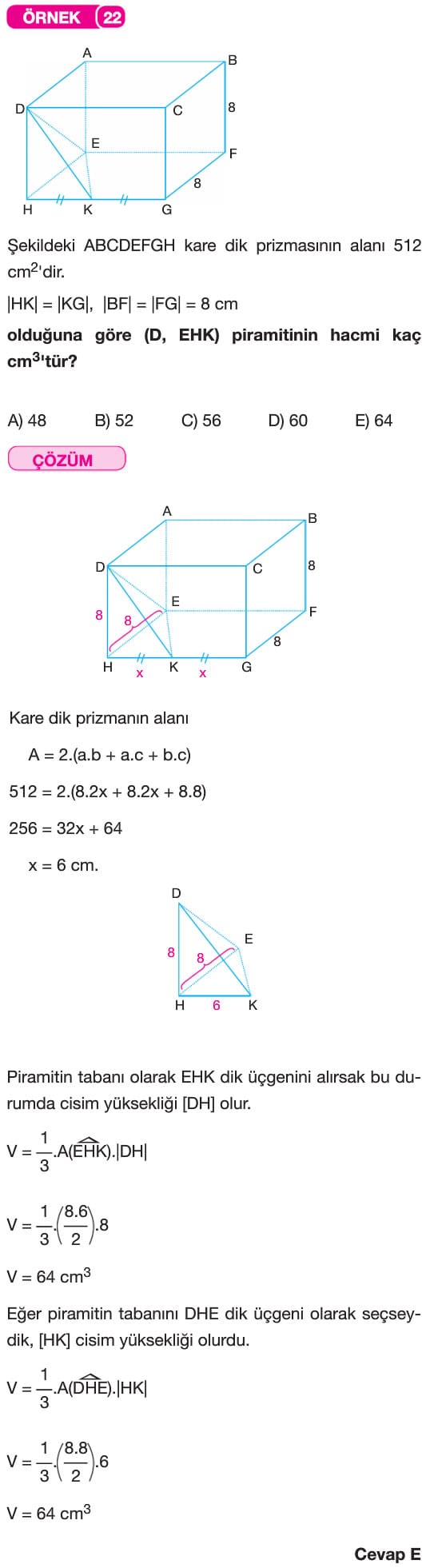
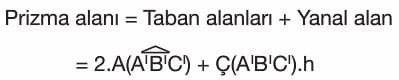Katı cisimler: Dik Prizma ve Dik Piramit 10. Sınıf
1. PRİZMALAR
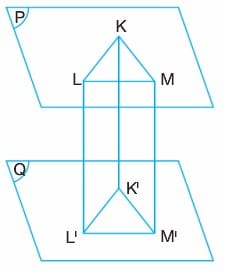
Birbirine paralel P ve Q düzlemleri içerisinde alınan iki eş çokgensel bölgenin tüm noktalarının karşılıklı olarak birleştirilmesiyle elde edilen içi dolu cisme prizma denir.
Şekildeki KLMK’L’M’ bir üçgen prizmadır. Tabanları üçgen olduğu için üçgen prizma olarak adlandırılır. Alt ve üst tabanlarının şekline göre prizmalar adlandırılır. Örneğin dikdörtgen prizma, kare prizma, düzgün altıgen prizma gibi.
Yukarıdaki şekilde
[K’L’], [K’M’], [L’M’] taban ayrıtlarıdır.
[KK’], [LL’], [MM’] ise prizmanın yanal ayrıtlarıdır.
K’L’M’ üçgeni prizmanın alt tabanı, KLM üçgeni prizmanın üst tabanı, KLL’K’, KMM’K’, LMM’L’ dörtgensel bölgeleri de prizmanın yanal alanıdır. Eğer bir prizmada yanal ayrıtlar taban düzlemine dik iniyorsa bu prizmaya dik prizma denir. Dik olmayan prizmalara ise eğik prizma denir. Alt ve üst taban düzlemleri arasındaki uzaklığa prizmanın yüksekliği denir.
Dik Prizmalar
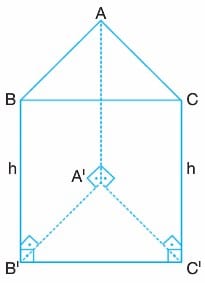
Yukarıdaki şekilde [AA’], [BB’] ve [CC’] yanal ayrıtları alt ve üst tabanlara diktir. Bu yüzden bu prizma bir üçgen dik prizmadır. Alt ve üst tabanlar özdeş olduğu için alanları eşittir. Yanal yüzler dikdörtgendir. Yanal alan kısaca şöyle bulunur.
Y.A. = Taban çevresi x Cisim Yüksekliği
Y.A = Ç(A’B’C’) x h
Prizmanın alanı ise tüm yüzeylerinin alanları toplamıdır.
Dik Prizmanın hacmi ise Taban Alanı x Yükseklik bağıntısı ile bulunur.
V = Taban Alanı x Yükseklik
Şimdi dik prizma çeşitlerini tanıyalım.
Küp
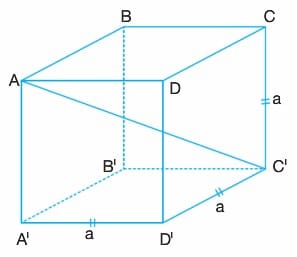
- Tüm ayrıtları eşit uzunlukta olan dikdörtgen prizmalara küp denir.
- 6 tane yüzey vardır ve yüzeylerin tamamı karedir.
- Her biri eşit uzunlukta 12 tane ayrıtı vardır.
- Küp içerisinde birbirine en uzak iki köşe arasındaki doğru parçasına cisim köşegeni denir.
Yukarıda çizilen küpün cisim köşegenleri [AC’], [BD’], [CA’] ve [DB’] dür. Cisim köşegenleri eşit uzunluktadır.
- Bir ayrıtı a cm olan yukarıdaki küpte,
1) Cisim köşegeni uzunluğu |AC’| = a√3 cm
2) Küpün alanı A = 6a2
3) Küpün hacmi v = a3‘tür.
Küpün yüzeylerinin açımış hâli ise aşağıdaki gibidir.
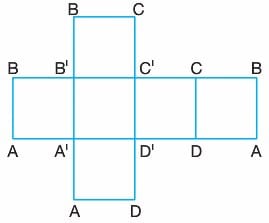
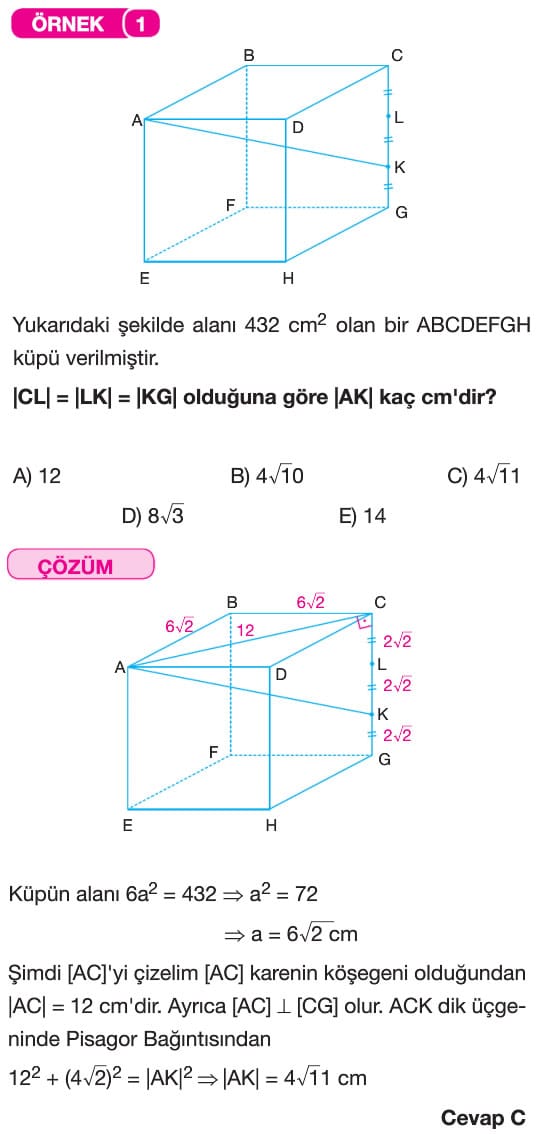
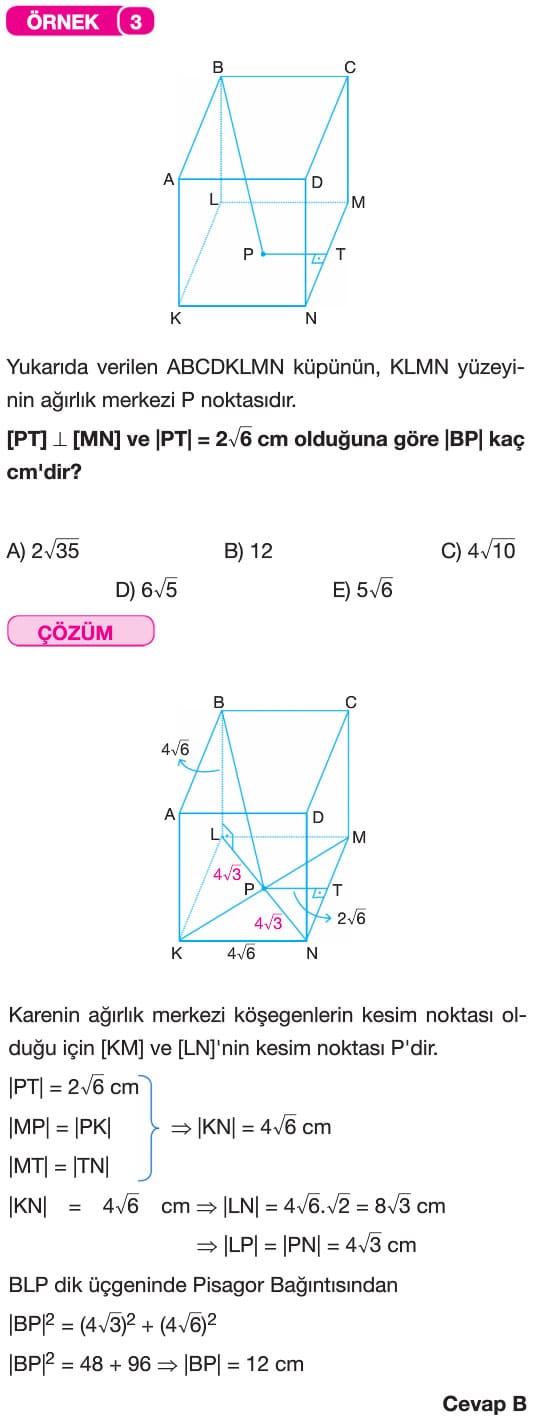
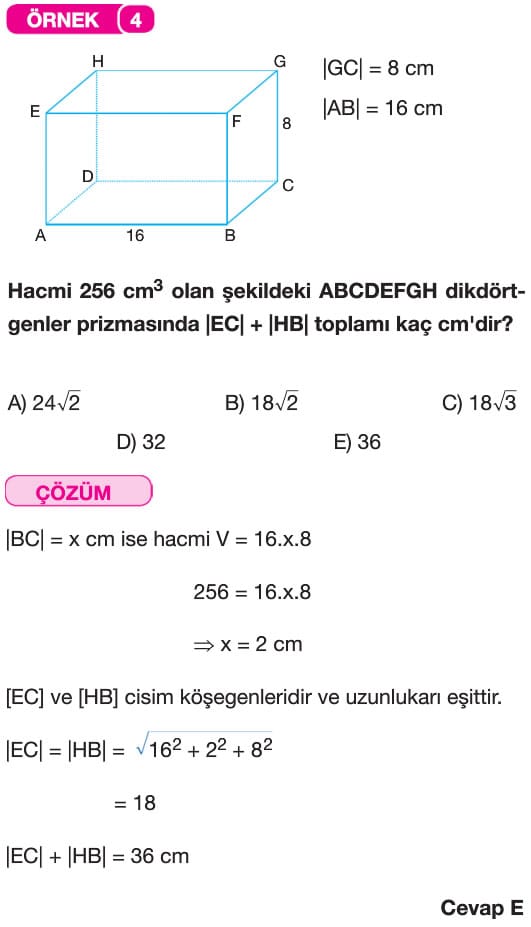
Çözümlü Sorular
Dikdörtgenler Prizması
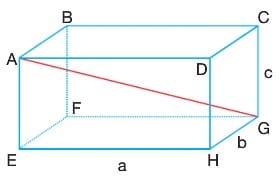
Çözümlü Sorular
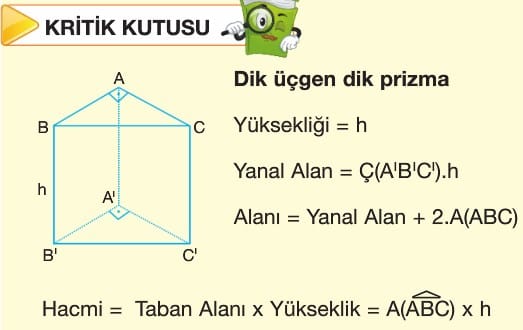
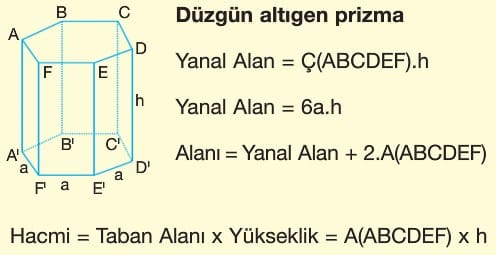
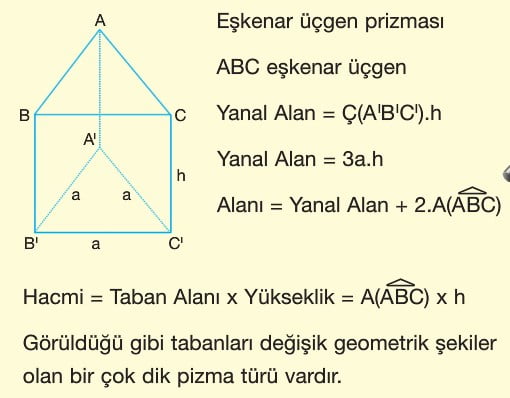
Dikkat: Tüm prizmaların alan ve hacminde aynı kurallar geçerlidir.
Yanal Alan = Taban Çevresi x Yükseklik
Alanı = Yanal Alan + 2 x Taban Alanı
Hacmi = TabanAlanı x Yükseklik
Çözümlü Sorular
2. PİRAMİT
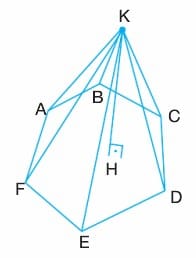
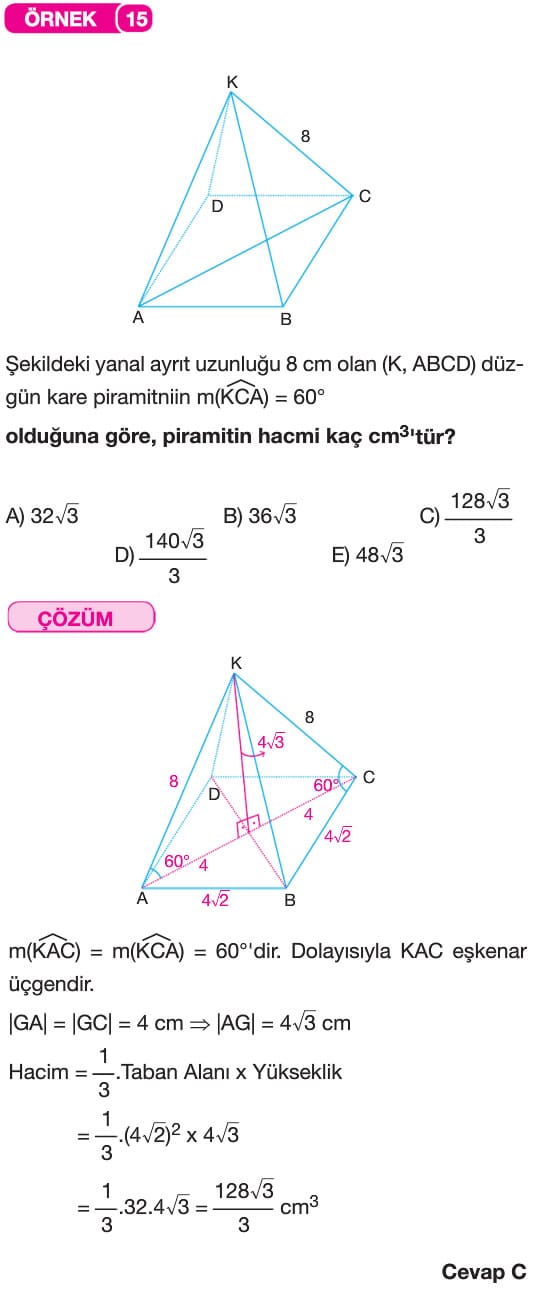
Bir düzlem üzerinde bulunan çokgensel bölgenin tüm noktalarının, bu düzlemin dışında bulunan bir noktayla birleştirilmesi sonucu oluşan cisme piramit denir. Buradaki (K, ABCDEF) bir altıgen piramittir. K noktası piramitin tepe noktası olup K noktasının taban düzlemine uzaklığı olan [KH]’na piramidin yüksekliği denir. [KA], [KB], [KC], [KD], [KE] ve [KF] piramitin yanal ayrıtlarıdır.
Piramitin Alanı = Taban Alanı + Yanal AlanPiramitin Hacmi = 13Taban Alanı x Yükseklik
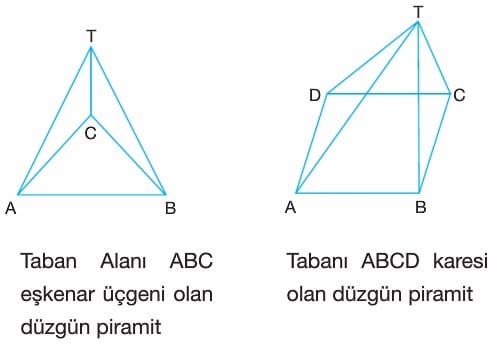
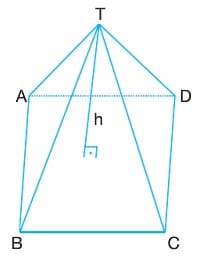
Düzgün Piramit
Tabanı düzgün çokgen olan ve yüksekliği bu düzgün çokgenin ağırlık merkezine inen piramitlere düzgün piramit denir.
Düzgün piramitlerin yanal ayrıtları eşit uzunlukta olduğu için tüm yanal yüzleri ikizkenar üçgendir.
Çözümlü Sorular
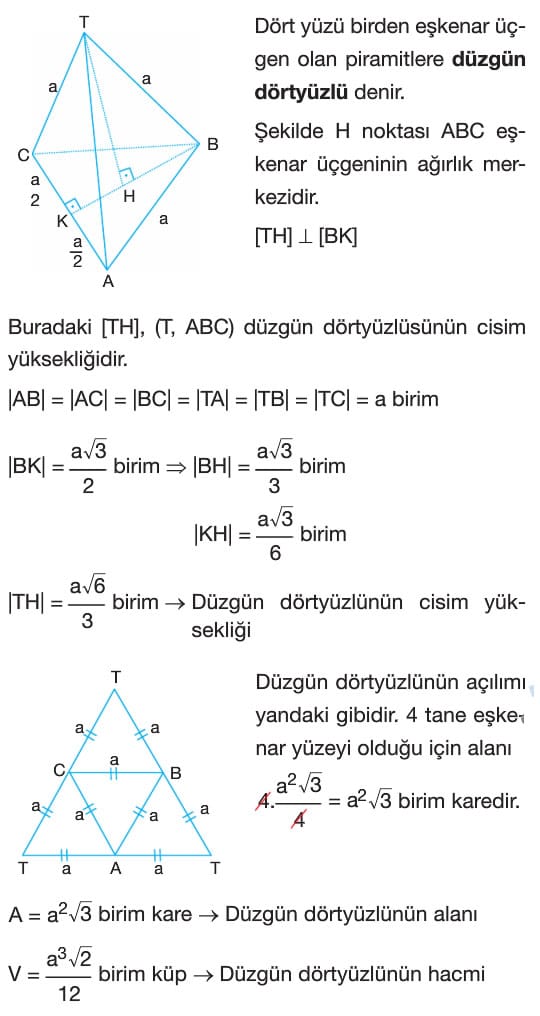
Düzgün Dörtyüzlü
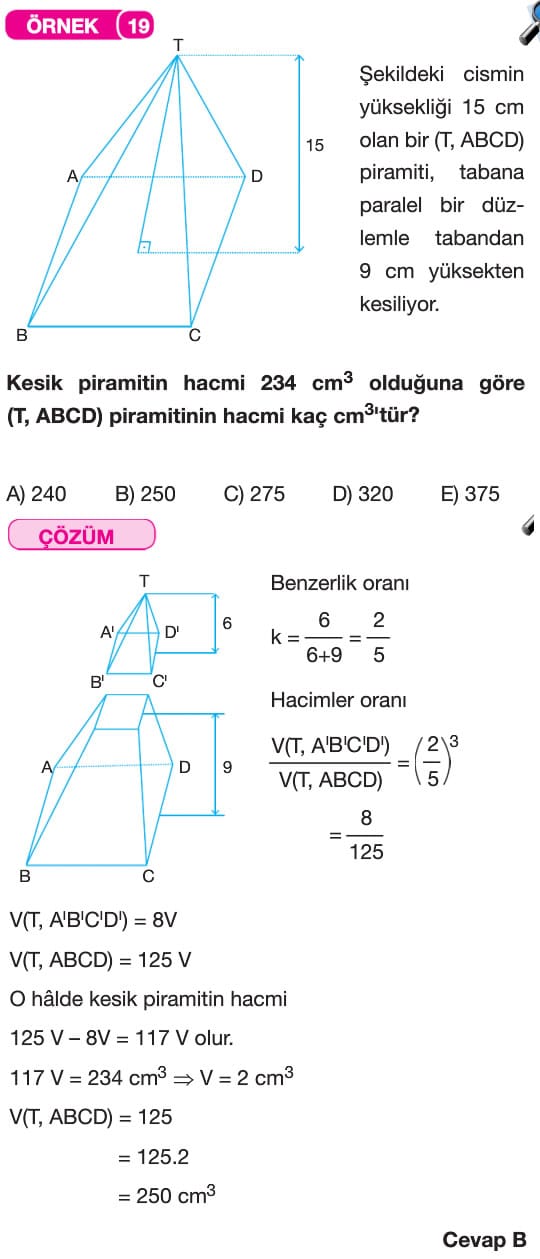
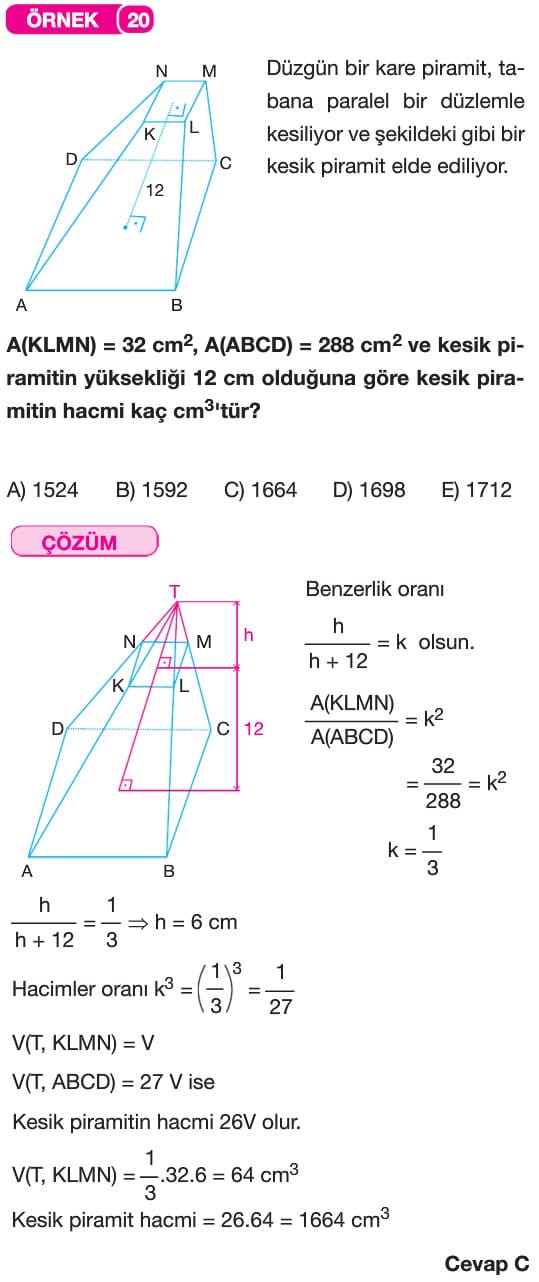
Kesik Piramit ve Piramit Benzerliği
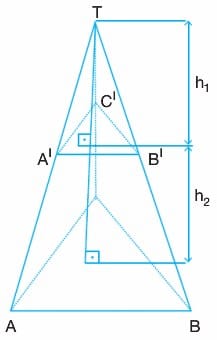
Bir piramiti tabana paralel olan bir düzlemle keselim. Taban ile düzlem arasında kalan cisme kesik piramit denir.
Şekildeki (T, A’B’C’) piramitinin yüksekliği h1, (T, ABC) piramitinin yüksekliği h1 + h2 olsun. Bu durumda (A’B’C’, ABC) kesik piramitinin yüksekliği h2 olur.
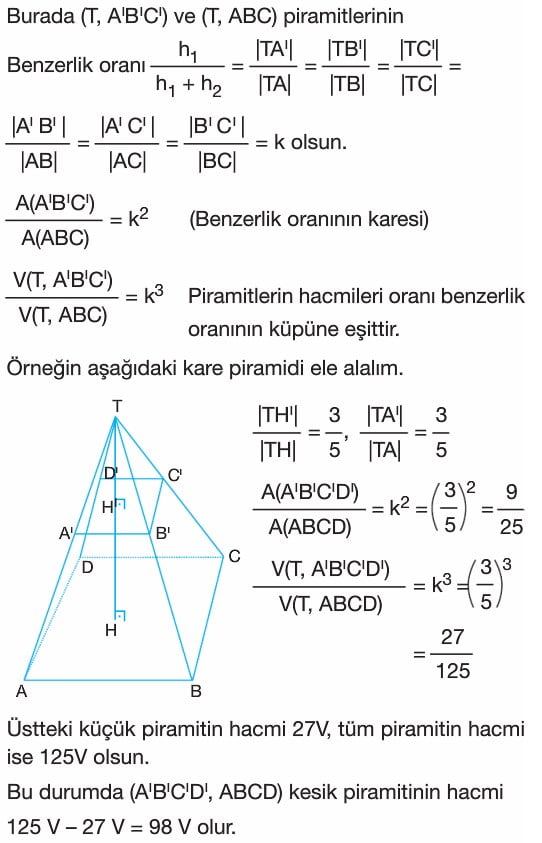
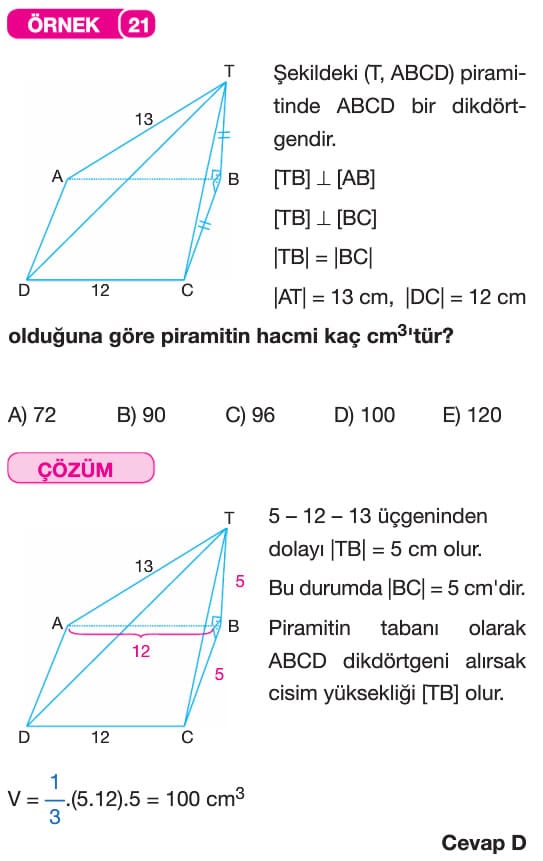
Düzgün Olmayan Piramitlerin Hacmi
Düzgün olmayan bir piramitin cisim yüksekliği genellikle tabanın ağırlık merkezine inmez. Hacim kuralları aynen geçerlidir. Yanal yüzler farklı alan değerlerine sahip olacağı için genellikle alan sorulmaz. Ancak sorulursa da yan yüz alanlarının tek tek hesaplanması gerekir.
Prizmalar Hocalara Geldik
Katı Cisimler Ekol Hoca
Çözümlü Örnek Test Soruları: Katı Cisimler – Dik Prizma ve Dik Piramit
1. Bir dik prizmanın tabanı dikdörtgen ve yüksekliği 8 cm’dir. Tabanın uzun kenarı 10 cm, kısa kenarı 6 cm olduğuna göre bu prizmanın hacmi kaç cm³’tür?
A) 240
B) 280
C) 360
D) 480
Çözüm:
Dik prizmanın hacim formülü:
Hacim = Taban Alanı × Yükseklik
Taban alanı = 10 × 6 = 60 cm²
Hacim = 60 × 8 = 480 cm³
Cevap: D
2. Aşağıdakilerden hangisi bir dik prizmanın özelliği değildir?
A) Tabanı çokgen olabilir.
B) Yan yüzleri dikdörtgendir.
C) Yan yüzleri üçgen olabilir.
D) Üç boyutlu bir geometrik şekildir.
Çözüm:
Bir dik prizmanın yan yüzleri her zaman dikdörtgendir. Eğer yan yüzleri üçgen olursa, o şekil bir piramit olur.
Cevap: C
3. Bir dik piramidin tabanı kare ve yüksekliği 12 cm’dir. Karenin bir kenarı 6 cm olduğuna göre, bu piramidin hacmi kaç cm³’tür?
A) 72
B) 144
C) 216
D) 432
Çözüm:
Dik piramidin hacim formülü:
Hacim = (Taban Alanı × Yükseklik) / 3
Taban alanı = 6 × 6 = 36 cm²
Hacim = (36 × 12) / 3 = 432 / 3 = 144 cm³
Cevap: B
4. Aşağıdaki ifadelerden hangisi yanlıştır?
A) Dik prizmanın tabanı bir çokgen olabilir.
B) Dik piramidin yalnızca bir tabanı vardır.
C) Dik piramidin yan yüzleri dikdörtgendir.
D) Dik prizmanın yan yüzleri dikdörtgendir.
Çözüm:
Dik piramidin yan yüzleri üçgen şeklindedir, dikdörtgen değildir. Bu nedenle yanlış ifade C şıkkıdır.
Cevap: C
5. Dik piramidin toplam yüzey alanı nasıl hesaplanır?
A) Taban alanı + yan yüzlerin toplam alanı
B) Yükseklik × taban kenarı
C) (Taban alanı × yükseklik) / 3
D) Taban çevresi × yükseklik
Çözüm:
Dik piramidin toplam yüzey alanı, taban alanı ile tüm yan yüzlerin alanlarının toplamıdır.
Cevap: A
Çözümlü Örnek Test Soruları 2
Soru 1
Aşağıdaki ifadelerden hangisi dik prizmalar için yanlıştır?
A) Yan yüzleri dikdörtgensel bölgedir
B) Tabanları eş ve paralel çokgenlerdir
C) Yan ayrıtları tabana diktir
D) Tüm yüzeyleri dikdörtgensel bölgedir
E) Yüksekliği yan ayrıt uzunluğuna eşittir
Çözüm:
Dik prizmalarda yan yüzler dikdörtgensel bölge olmak zorundadır, ancak tabanlar farklı çokgenler olabilir (üçgen, beşgen gibi). Bu nedenle “tüm yüzeyleri dikdörtgensel bölgedir” ifadesi yanlıştır.
Doğru Cevap: D
Soru 2
Taban ayrıtları 5 cm ve 12 cm, yüksekliği 10 cm olan dikdörtgenler prizmasının hacmi kaç cm³’tür?
A) 120
B) 300
C) 480
D) 600
E) 720
Çözüm:
Dikdörtgenler prizmasının hacmi = Taban alanı × Yükseklik
= (5 × 12) × 10 = 60 × 10 = 600 cm³
Doğru Cevap: D
Soru 3
Taban alanı 36 cm² olan bir dik kare piramidin yüksekliği 8 cm ise, hacmi kaç cm³’tür?
A) 96
B) 108
C) 144
D) 288
E) 324
Çözüm:
Dik piramidin hacmi = (Taban alanı × Yükseklik)/3
= (36 × 8)/3 = 288/3 = 96 cm³
Doğru Cevap: A
Soru 4
Bir dikdörtgenler prizmasının boyutları 3 cm, 4 cm ve 5 cm’dir. Bu prizmanın yüzey alanı kaç cm²’dir?
A) 47
B) 60
C) 72
D) 94
E) 120
Çözüm:
Yüzey alanı = 2(ab + ac + bc) = 2(3×4 + 3×5 + 4×5)
= 2(12 + 15 + 20) = 2×47 = 94 cm²
Doğru Cevap: D
Soru 5
Tabanı eşkenar üçgen olan bir dik prizmanın taban kenarı 6 cm, yüksekliği 10 cm’dir. Bu prizmanın hacmi kaç cm³’tür? (√3 ≈ 1,73)
A) 90
B) 103,8
C) 120
D) 155,7
E) 180
Çözüm:
Eşkenar üçgen alanı = (a²√3)/4 = (36×1,73)/4 ≈ 15,57 cm²
Hacim = Taban alanı × Yükseklik ≈ 15,57 × 10 ≈ 155,7 cm³
Doğru Cevap: D
Soru 6
Bir dik kare piramidin taban ayrıtı 12 cm, yan yüz yüksekliği 10 cm’dir. Bu piramidin yanal alanı kaç cm²’dir?
A) 120
B) 240
C) 360
D) 480
E) 600
Çözüm:
Bir yan yüz alanı = (Taban ayrıtı × Yan yüz yüksekliği)/2
= (12 × 10)/2 = 60 cm²
Yanal alan = 4 × 60 = 240 cm² (kare piramitte 4 yan yüz vardır)
Doğru Cevap: B