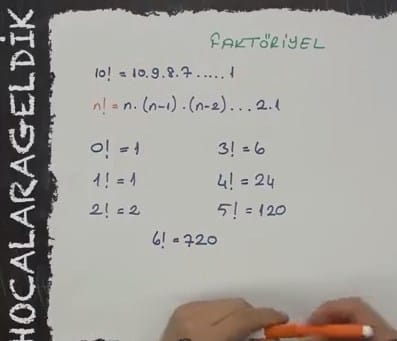MUTLAK DEĞER
ÜSLÜ SAYILAR
KÖKLÜ SAYILAR
ÇARPANLARA AYIRMA
ORAN – ORANTI
PROBLEMLER
MANTIK
KÜMELER
KARTEZYEN ÇARPIM
FONKSİYONLAR
POLİNOMLAR
İKİNCİ DERECEDEN DENKLEMLER
KARMAŞIK SAYILAR
PARABOL
SAYMA – PERMÜTAYON – KOMBİNASYON
BİNOM
OLASILIK
VERİ
Soru: a, b, c birbirinden farklı rakamlardır.
4a – 3b + 7c
ifadenin alabileceği en büyük değer kaçtır?
A) 54 B) 62 C) 92 D) 94 E) 95
Çözüm: ifadesinin en büyük olması için a ve c en büyük, b ise en küçük değeri almalıdır. Bu değerleri a, b ve c’nin katsayılarına bakarak seçmek gerekir. a = 8, b = 0 ve c = 9 olursa koşul sağlanır.
4.8-3.0+7.9=95 bulunur. Yanıt E
Soru: x ve y birer doğal sayı olmak üzere,
x + y = 13
olduğuna göre, x – y çarpımının en büyük değeri kaçtır?
A) 12 B) 36 C) 24 D) 42 E) 40
Çözüm: Toplamları sabit olan iki sayının çarpımlarının en büyük olması için sayılar birbirine eşit ya da yakın seçilmelidir.
x=6 ve y=7 için x.y=42 olur. Yanıt D
Soru: x ve y birer doğal sayı olmak üzere,
x . y = 24
olduğuna göre, x + y toplamının en küçük değeri kaçtır?
A) 25 B)14 c)11 D)10 E)8
Çözüm: Çarpımları sabit olan iki sayının toplamlarının en küçük olması için sayılar birbirine en yakın seçilmelidir.
x.y=24 ise x=6 ve y=4 için x+y=10 olur. Yanıt D
Soru: a ve b birer tam sayıdır.
a – b = 36
olduğuna göre, a + b toplamının alabileceği en değer kaçtır?
A) -37 B) -20 C) 0 D) 12 E) 13
Çözüm: a ve b tam sayı olduğu için, her ikisi de negatif seçilirse toplamları en az olur.
a.b=36 ise a=-36 ve b=-1 için a + b = -37 bulunur. Yanıt A
Soru: a, b, c birer pozitif tam sayı olmak üzere,
a-b=10 ve b.c=15
olduğuna göre, a + b + c toplamı en fazla kaçtır?
A)10 B) 15 C)18 D)25 E) 26
Çözüm: Burada ortak olan b sayısıdır. b en az olmalıdır ki a ve c en fazla olsun. Bu durumda a + b + c toplamı da en fazla olur. b=1 için ve a=10 ve c=15 olur. a+b+c = 10+1+15=26 bulunur. Yanıt E
Soru: a, b, c sıfırdan büyük rakamlar
3a = 2b ve Sb = c olduğuna göre, a + b + c toplamı kaçtır?
A)10 B)11 c)12 D)13 E)14
Çözüm: 3a = 2b ise a = 2k ve b = 3k olsun.
3b = 3k için c = 33k = 9k olur.
Sıfırdan büyük rakam dediği için k = 1 alındığında
a=2, b=3 ve c=9 bulunur.
a+b+c = 2+3+9=14 olur. Yanıt E
Soru: Sayı doğrusu üzerinde sırasıyla işaretlenmiş x, y, z ve t sayılarının toplamı 60’dır. Bu sayıların en büyüğü t olmak üzere, t’nin x, y ve z sayılarının her birine olan uzaklıkları toplamı 40’dır. Buna göre, t sayısı kaçtır?
A) 10 B) 15 C) 20 D) 25 E) 30
Çözüm: t sayısının x sayısına uzaklığı t- x, t sayısının y sayısına uzaklığı t- y ve t sayısının z sayısına uzaklığı t- z dir.
t-x+t-y+t-z = 40 ise, x+y+z = 3t-40 ve x+y+z+t = 60
3t-40+t = 60 ise 4t = 100 ve t=25 olur. Yanıt D
Soru: Bir öğretmen tahtaya bir toplama işlemi yazıyor ve öğrencilerinden bu işlemi yapmalarını istiyor. Fadıl, Emel, Hakan, Kebuter ve Aslı’nın yaptıkları toplama işlemi sonucu buldukları sayılar aşağıda verilmiştir.
Fadıl: 43 Emel: 38 Hakan: 62
Kebuter: 33 Aslı: 55
Öğretmenleri toplama işlemindeki hatalarını gelişi güzel söylüyor.
Yapılan hatalar 18, 4, 13, 8 ve 11 olduğuna göre, bulunması gereken sayı kaçtır?
A) 49 B) 51 C) 54 D) 55 E) 56
Çözüm: Tüm çocukların aynı sonucu bulması gerektiği için verilen sayılarla aşağıdaki işlemleri yaptığımızda;
43+B=38+13=62-11=33+18=55-4 olduğu için bulunması gereken sayı 51’dir. Yanıt B
Soru: Ardışık iki pozitif tam sayı ile ilgili aşağıdaki ifadelerden hangileri doğrudur?
l. Ardışık 2 pozitif tam sayının çarpımı çifttir.
Il. Ardışık 2 pozitif tam sayının toplamı tektir.
llI. Ardışık 2 tek tam sayının çarpımının 1 eksiği tam karedir.
IV. Ardışık 2 tek tam sayının çarpımının 1 fazlası tam karedir.
A) Yalnız I B) Yalnız III C) l, II ve lV
D) I, Il ve lll E) ll ve III
Çözüm: Sayılar 2 ve 3 olsun.
I. 2 . 3 = G çifttir. (Doğru)
II. 2 + 3 = 5 tektir. (Doğru)
IlI. ve IV. öncül için ardışık iki tek tam sayı olarak 1 ile 3 ü alalım.
IlI. 1 . 3 -1 = 2 sayısı tam kare değil. (Yanlış)
IV. 1 ~ 3 + 1 = 4 sayısı tam karedir. (Doğru) Yanıt C