11. sınıf Matematik
11. Sınıf Matematik konu anlatımı ve soru çözümleri videoları izleyebilirsiniz.
1. ÜNİTE: TRİGONOMETRİ
- Yönlü Açılar
- Trigonometrik Fonksiyonlar
- Trigonometrik Özdeşlikler
- Kosinüs Teoremi ve Sinüs Teoremi
- Trigonometrik Fonksiyonların Periyotları
- Trigonometrik Fonksiyonların Grafikleri
- Ters Trigonometrik Fonksiyonlar
2. ÜNİTE: DOĞRUNUN ANALİTİK İNCELENMESİ
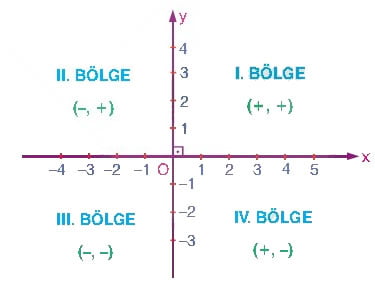
A. Analitik Geometri Hazırlık
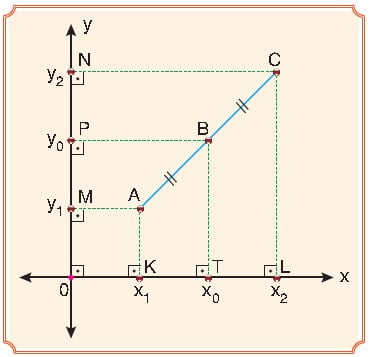
B. İki Nokta Arasındaki Uzaklık
C. Doğru Parçasını Belli Bir Oranda Bölen Noktanın Koordinatları
- Bir Doğru Parçasının Orta Noktası
- Bir doğru parçasını belli bir oranda içten ve dıştan bölen noktanın koordinatları
D. Analitik Düzlemde Doğrular
E. Bir Noktanın Bir Doğruya Uzaklığı ve Paralel İki Doğru Arasındaki Uzaklık
3. ÜNİTE: FONKSİYONLARDA UYGULAMALAR
- Fonksiyonlarla İlgili Uygulamalar
- İkinci Dereceden Fonksiyonların Grafikleri (Parabol)
- Fonksiyonların Dönüşümleri
4. ÜNİTE: DENKLEM VE EŞİTSİZLİK SİSTEMLERİ (İkinci Dereceden İki Bilinmeyenli Denklem Sistemleri, İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler ve Eşitsizlik Sistemleri)
5. ÜNİTE: ÇEMBER VE DAİRE
- Çemberin Temel Elemanları ve Çemberde Kiriş Özellikleri
- Çemberde Açı Çevrel Çember ve Sinüs Teoremi
- Çemberde Teğet
- Dairenin Çevresi ve Alanı
6. ÜNİTE: KATI CİSİMLER
7. ÜNİTE: OLASILIK
11. Sınıf Matematik konuları soruları çözümleri ders notları
Soru: Şekillerdeki küreleri inceleyip temel elemanlarını gösterelim.
Çözelim: Yandaki K merkezli a yarıçaplı daire, kürenin ortasından değil, herhangi bir yerinden kesilip de oluşturulmuştur. Bu nedenle kürenin yarıçapı ile bu dairenin yarıçapı farklıdır. Yandaki O merkezli kürenin tam merkezinden geçen düzlem, küreyi iki eş parçaya ayırmıştır. Burada oluşan dairenin yarıçapı, kürenin yarıçapıdır. Tam ortasından kesilerek oluşturulan yarım kürelerdeki daireler, büyük dairelerdir.
Öğrenelim: Kürenin hacim bağıntısını elde edelim. Bunun için r yarıçaplı içi dolu küre ile taban yarıçapı r ve yüksekliği 2r olan içi dolu silindirden faydalanalım. Yandaki şekilde olduğu gibi silindirin içinden tabanları silindirin tabanları olan eş konileri çıkartalım. Geriye kalan hacim ile kürenin hacimlerini karşılaştıralım. Kürenin ve silindirin yarısını alarak kürenin merkezinden ve silindirin içindeki konilerin ortak tepe noktasından h birim uzaklıkta bir düzlemle kürenin ve dik dairesel silindirin aşağıdaki gibi ara kesitlerinin alanlarını hesaplayalım. Aşağıdaki fotoğraflarda da görüldüğü gibi r yarıçaplı kürenin bir düzlemde arakesiti, a yarıçaplı bir dairedir.
Öğrenelim: Kürenin yüzey alanının nasıl bulunacağını belirleyelim. Bunun için bir küreyi tepe noktası kürenin merkezinde ve tabanı küre yüzeyinde olan dik piramitle ve ayırıp aşağıdaki gibi bir küre oluşturalım. Bu piramitleri A1, A2, …, An olarak isimlendirirsek çok sayıda kullanacağımız tüm piramitlerin hacmi yaklaşık olarak kürenin hacmine eşit olacaktır.