x² + 1 = 0 denkleminin çözüm kümesini bulmaya çalışalım.
x² + 1 = 0 ise x² = -1 olacağından bu denklemi sağlayan bir gerçek sayı değerinin olmadığını görürüz. O halde bu denklemin gerçek sayılar kümesindeki çözüm kümesi Ø dir. Bu denklemin çözüm kümesini bulabilmek için karmaşık sayılar isimli yeni bir küme tanımlanmıştır. Karmaşık sayılar kümesi C ile gösterilir ve reel sayılar kümesini kapsar.

Bilgi: a ve b gerçek sayılar, i sanal birim olmak üzere, a + b.i şeklindeki sayılara karmaşık sayı denir ve genellikle z ve w harfleriyle gösterilir.

z = a + b.i yazılışına z karmaşık sayısının “standart biçimi“, a sayısına z nin reel kısmı, b sayısına da z nin imajiner (sanal) kısmı denir ve
a = Re(z), b = Im(z) şeklinde gösterilir.

C={z: z = a+b.i, a ∈ R, b ∈ R, i sanal birim} kümesine karmaşık sayılar kümesi denir.

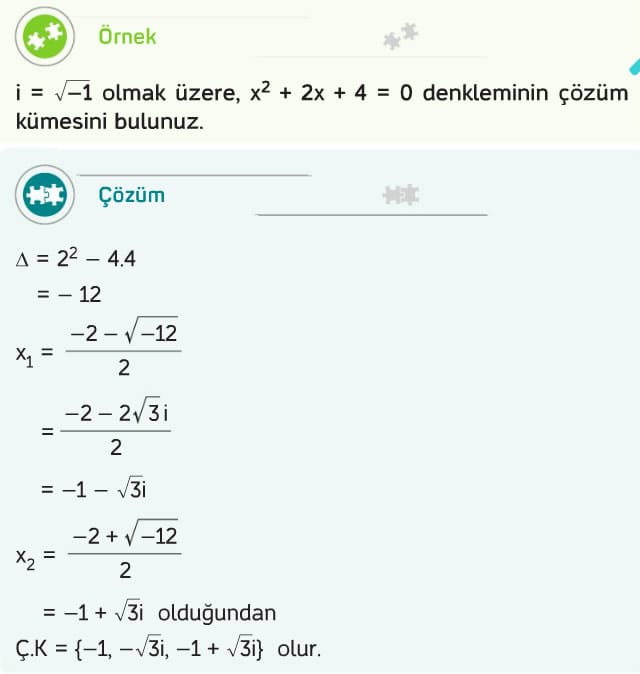
Not: Gerçek katsayılı bir ikinci derece denklemin kökleri karmaşık sayı ise bu kökler birbirinin eşleniğidir.

i nin Kuvvetleri

i¹ = i, i² = -1, i³ = -i, i⁴ = 1 olduğundan i nin bir tam sayı kuvveti hesaplanırken üs yerine üssün 4 ile bölümünden kalan yazılarak sonuca gidilir.

i²² = i² = -1, i⁴³ = i³ = -i

Karmaşık Sayılarda Toplama ve Çıkarma işlemi

Karmaşık sayılarda toplama ve çıkarma işlemi yapılırken reel kısımlar kendi aralarında, sanal kısımlar kendi aralarında toplanır ya da çıkarılır.

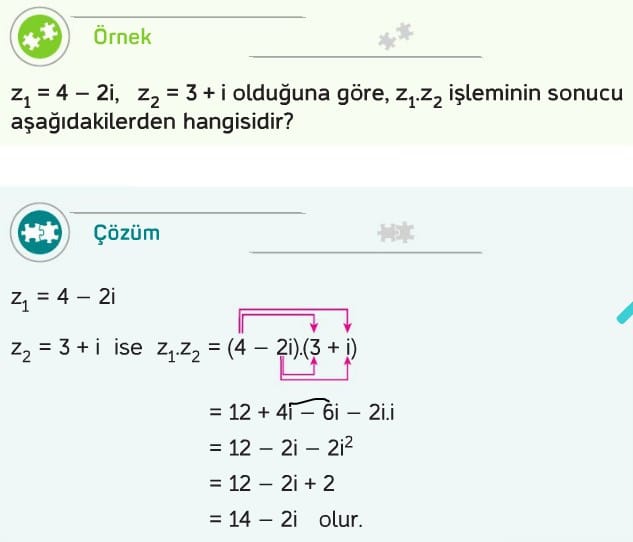
Karmaşık Sayılarda Çarpma İşlemi

Karmaşık sayılarda çarpma işlemi yapılırken birinci sayının tüm terimleri ile ikinci sayının tüm terimleri sırayla çarpılır.

Karmaşık sayılarda Bölme İşlemi

Karmaşık sayılarda bölme işlemi yapılırken pay ve payda, paydadaki karmaşık sayının eşleniği ile genişletilir.

Çözümlü Örnek Test Soruları: Karmaşık Sayılar

1. Aşağıdaki sayılardan hangisi bir karmaşık sayıdır?
A) 5
B) -3
C) 2i
D) 0

Çözüm:
Karmaşık sayılar, z = a + bi formunda yazılır ve a reel, b ise sanal kısmı ifade eder. 2i bir karmaşık sayıdır çünkü sanal bir kısmı vardır.
Doğru cevap: C

---

2. z = 3 + 4i karmaşık sayısının eşleniği aşağıdakilerden hangisidir?
A) 3 – 4i
B) 3 + 4i
C) -3 – 4i
D) -3 + 4i

Çözüm:
Bir karmaşık sayının eşleniği, sanal kısmının işaretinin değiştirilmesiyle elde edilir.
z = 3 + 4i için eşleniği z’ = 3 – 4i olur.
Doğru cevap: A

---

3. z = 2 + 3i ve w = 1 – 2i ise z + w işleminin sonucu nedir?
A) 3 + i
B) 1 + 5i
C) 2 – i
D) 3 – i

Çözüm:
Karmaşık sayılar toplanırken reel kısımlar ve sanal kısımlar ayrı ayrı toplanır:
z + w = (2 + 1) + (3i – 2i) = 3 + i.
Doğru cevap: A

---

4. z = 4 + 3i karmaşık sayısının modülü (büyüklüğü) nedir?
A) 5
B) 7
C) 25
D) 13

Çözüm:
Bir karmaşık sayının modülü, |z| = √(a² + b²) formülüyle bulunur.
z = 4 + 3i için |z| = √(4² + 3²) = √(16 + 9) = √25 = 5.
Doğru cevap: A

---

5. z = 1 + i karmaşık sayısının karesi z² aşağıdakilerden hangisidir?
A) 1 + 2i
B) 2i
C) 2 + 2i
D) 0

Çözüm:
z = 1 + i için:
z² = (1 + i)² = 1² + 2 × 1 × i + i² = 1 + 2i + (-1) = 2i.
Doğru cevap: B

---

Örneğin; Sanal birim kullanarak x² + 1 = 0 denklemini çözelim.
x²+1=0 ise x²=-1
x² = i²
x = i veya x = -i bulunur. Buradan denklemin karmaşık sayılardaki çözüm kümesi {-i, i} olur.

Bir z karmaşık sayısının sanal kısmının işaretinin değiştirilmesiyle elde edilen karmaşık sayıya z nin eşleniği denir ve ile gösterilir.

Karesi –1 olan sayıya sanal (imajiner) sayı birimi denir ve i ile gösterilir.

a ve b gerçek sayı olmak üzere, z = a + b.i biçiminde gösterilen sayılara karmaşık sayılar denir.

Karmaşık sayılar konu başlıkları:

• Karmaşık sayı tanımı
• İki karmaşık sayının eşitliği
• Karmaşık düzlem
• Bir karmaşık sayının eşleniği
• İkinci dereceden bir denklemin sanal kökleri
• Karmaşık sayılarda dört işlem
• Bir karmaşık sayının modülü (Mutlak değeri)
• İki karmaşık sayı arasındaki uzaklık
• Karmaşık sayıların kutupsal biçimi (Trigonometrik biçimi)
• Kutupsal biçimde işlemler
• Bir karmaşık sayının kuvveti
• Bir karmaşık sayının kökleri