Kare ve Özellikleri, Karenin Alanı 10. Sınıf

10. sınıf Matematik Konuları Konu Anlatımları Matematik
04.02.2025
0

Bütün kenar uzunlukları eşit ve bütün açıları 90° olan dörtgene kare denir.

KARENİN ÖZELLİKLERİ

Özellik:

Çözümlü Sorular

Karenin Alanı

Çözümlü Sorular

Kare Özellikleri ve Alanı Şenol Hoca

Kare Özellikleri ve Alanı Ekol Hoca

Çözümlü Örnek Test Soruları

1. Bir karenin bir kenar uzunluğu 8 cm’dir. Bu karenin alanı kaç cm²’dir?

A) 16
B) 32
C) 64
D) 128

Çözüm:
Karenin alanı, A = a² formülü ile hesaplanır.
Verilen karenin bir kenarı 8 cm olduğuna göre:
A = 8 × 8 = 64 cm²
Doğru cevap: C

2. Alanı 100 cm² olan bir karenin çevresi kaç cm’dir?

A) 20
B) 30
C) 40
D) 50

Çözüm:
Karenin alanı A = a² formülü ile hesaplanır.
a² = 100 olduğuna göre, her iki tarafın karekökünü alırsak:
a = 10 cm
Karenin çevresi Ç = 4a formülünden bulunur:
Ç = 4 × 10 = 40 cm
Doğru cevap: C

3. Bir karenin çevresi 48 cm’dir. Bu karenin alanı kaç cm²’dir?

A) 64
B) 81
C) 100
D) 144

Çözüm:
Karenin çevresi Ç = 4a formülü ile hesaplanır.
4a = 48 olduğuna göre, her iki tarafı 4’e bölelim:
a = 12 cm
Alan formülü A = a² olduğuna göre:
A = 12 × 12 = 144 cm²
Doğru cevap: D

4. Karenin köşegen uzunluğu 10√2 cm ise, bu karenin alanı kaç cm²’dir?

A) 25
B) 50
C) 100
D) 200

Çözüm:
Karenin köşegen uzunluğu d = a√2 formülüyle hesaplanır.
10√2 = a√2 eşitliğinden her iki tarafı √2’ye bölelim:
a = 10 cm
Karenin alanı A = a² formülünden:
A = 10 × 10 = 100 cm²
Doğru cevap: C

5. Bir karenin alanı 196 cm² ise, köşegen uzunluğu kaç cm’dir?

A) 10
B) 14
C) 14√2
D) 28

Çözüm:
Karenin alanı A = a² formülü ile hesaplanır.
a² = 196 olduğuna göre karekök alırsak:
a = 14 cm
Karenin köşegen uzunluğu d = a√2 formülüyle hesaplanır:
d = 14√2 cm
Doğru cevap: C

ETİKETLER: ,
BİR YORUM YAZIN

ZİYARETÇİ YORUMLARI - 0 YORUM

Henüz yorum yapılmamış.

10. sınıf Kare Özellikleri Alanı konu anlatımı soruları çözümleri Matematik özet

 

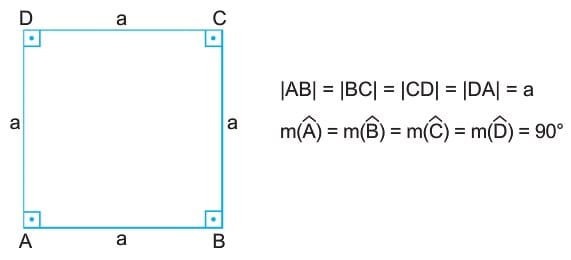
  • Bir ABCD karesinde tüm kenar uzunlukları birbirine eşittir. Yani;
    |AB| = |BC| = |CD| = |DA| = a
  • Bir ABCD karesinde tüm açılar birbirine eşit ve ölçüleri 90 derecedir. Yani;
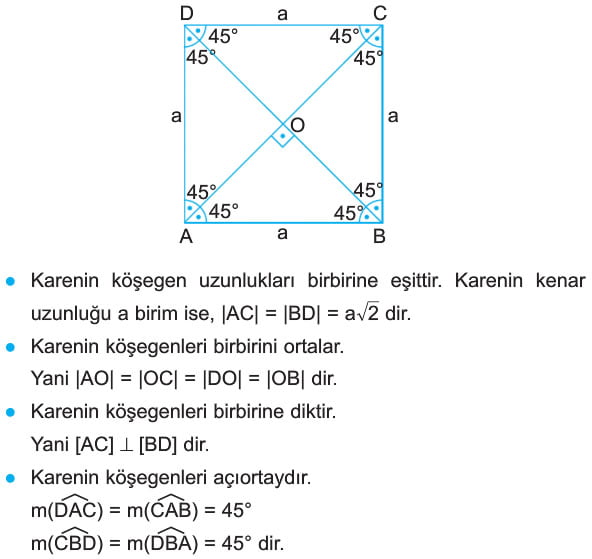
    m(A) = m(B) = m(C) = m(D) = 90°
  • Karenin köşegen uzunlukları birbirine eşittir. Karenin kenar uzunluğu a birim ise, |AC| = |BD| = a√2 dir.
  • Karenin köşegenleri birbirini ortalar.
    Yani |AO| = |OC| = |DO| = |OB| dir.
  • Karenin köşegenleri birbirine diktir.
    Yani [AC] dik [BD] dir.
  • Karenin köşegenleri açıortaydır.
    m(DAC) = m(CAB) = 45°
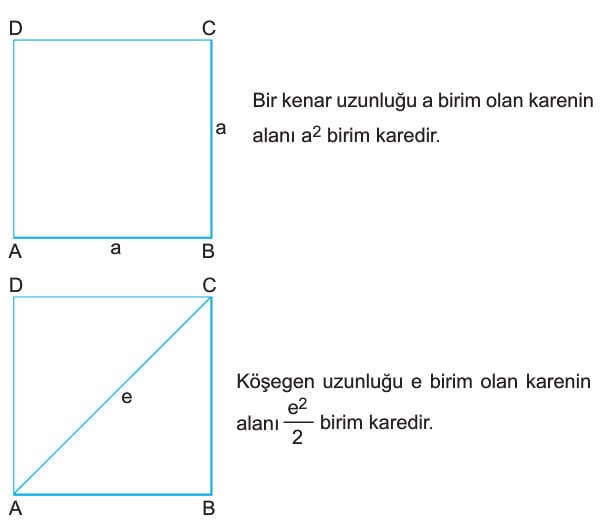
    m(CBD) = m(DBA) = 45° dir.
  • Bir kenar uzunluğu a birim olan karenin alanı a2 birim karedir.Köşegen uzunluğu e birim olan karenin alanı e2 / 2 birim karedir.
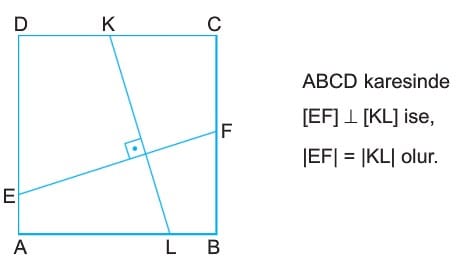
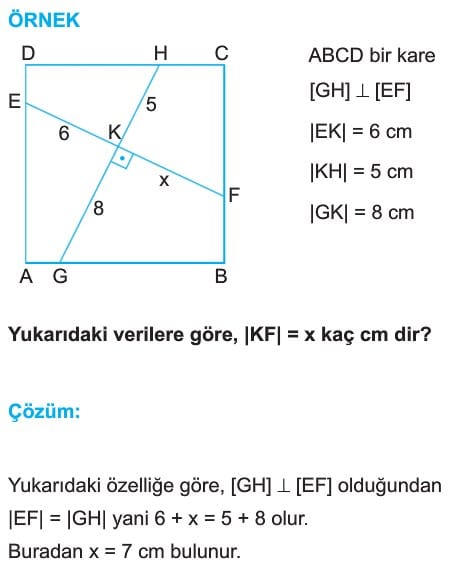
  • Karede köşegenler dik kesişirse uzunlukları eşittir.

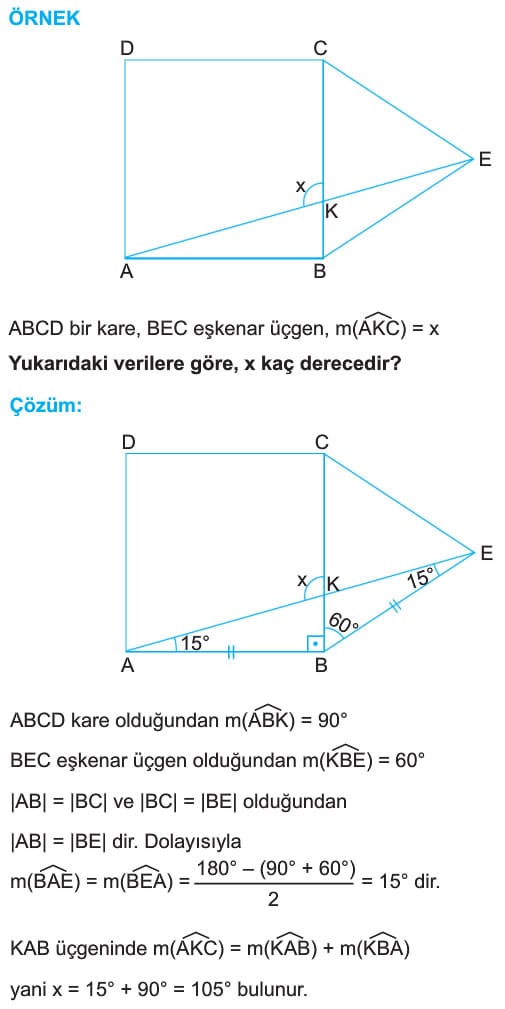
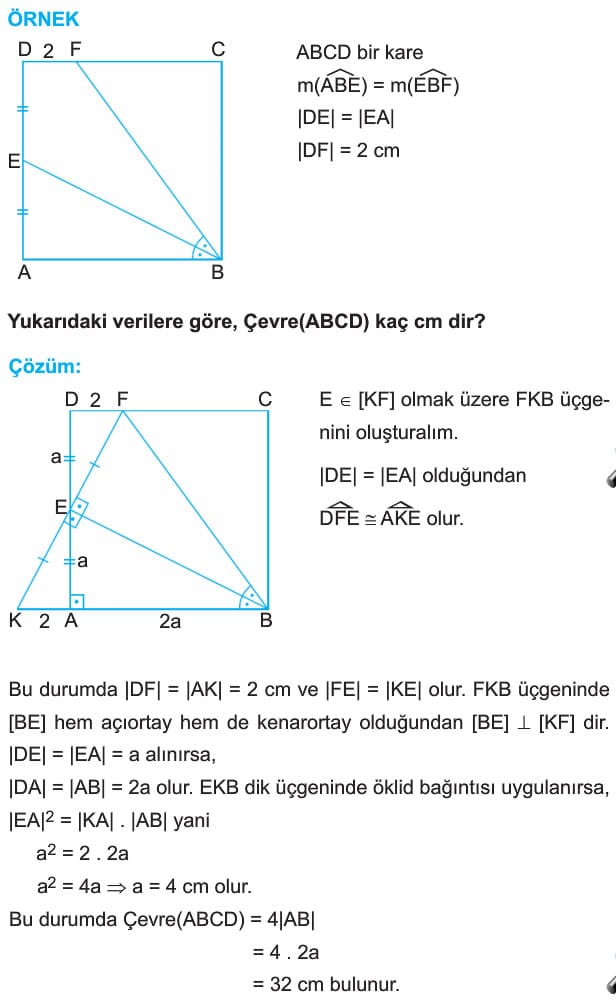
ÖRNEK: ABCD bir kare, BEC eşkenar Üçgen, m(AKC) = x
Yukarıdaki verilere göre, x kaç derecedir?
Çözüm: ABCD kare olduğundan m(ABK) = 90°
BEC eşkenar üçgen olduğundan m(KBE) = 60°
|AB| = |BC| ve |BC| = |BE| olduğundan
|AB| = |BE| dir. Dolayısıyla
m(BAE) = m(BEA) = [180° - (90° + 60°)] / 2 = 15° dir.
KAB üçgeninde m(AKC) = m(KAB) + m(KBA)
yani x = 15° + 90° = 105° bulunur.

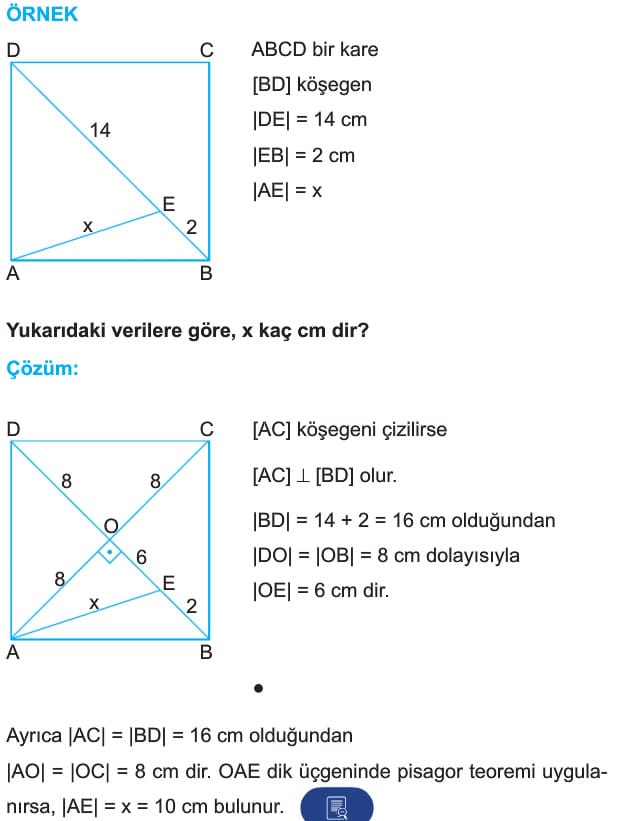
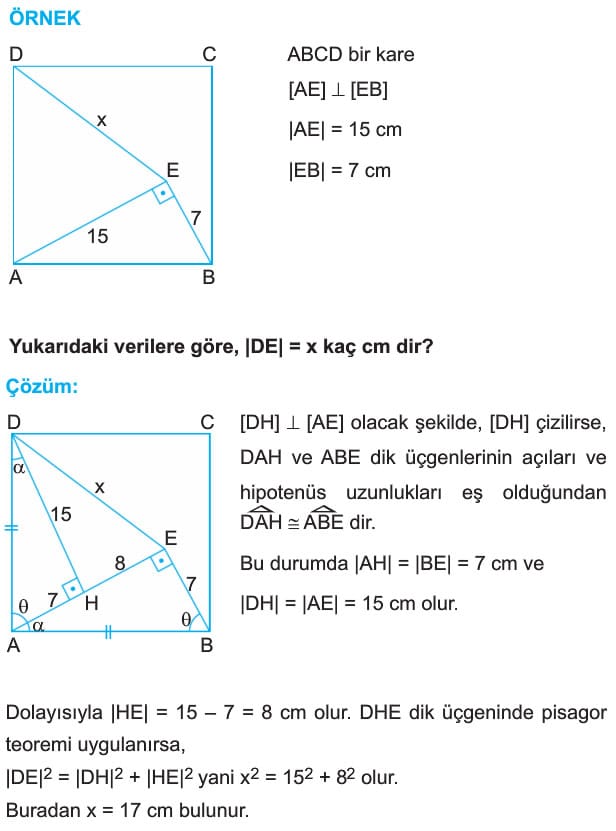
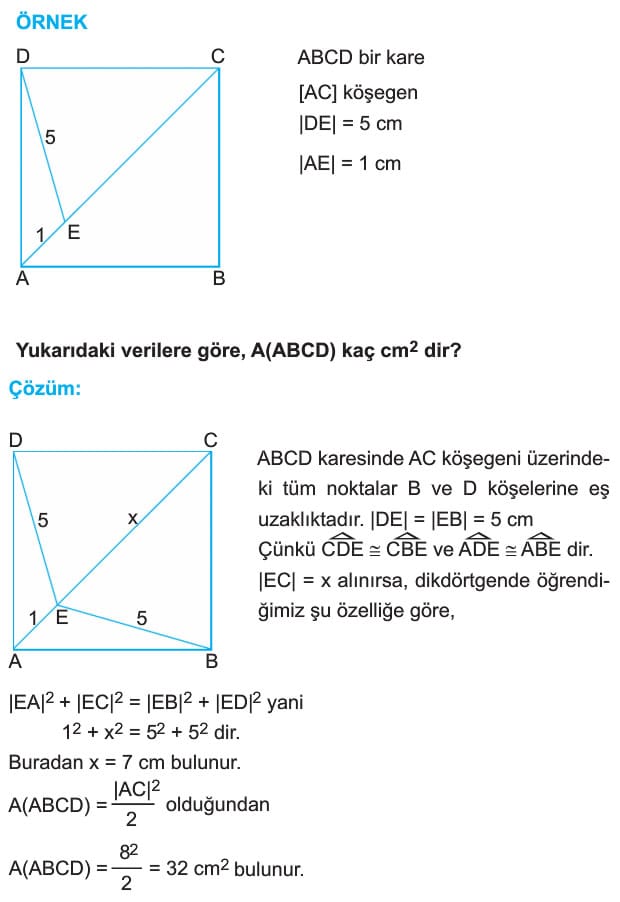
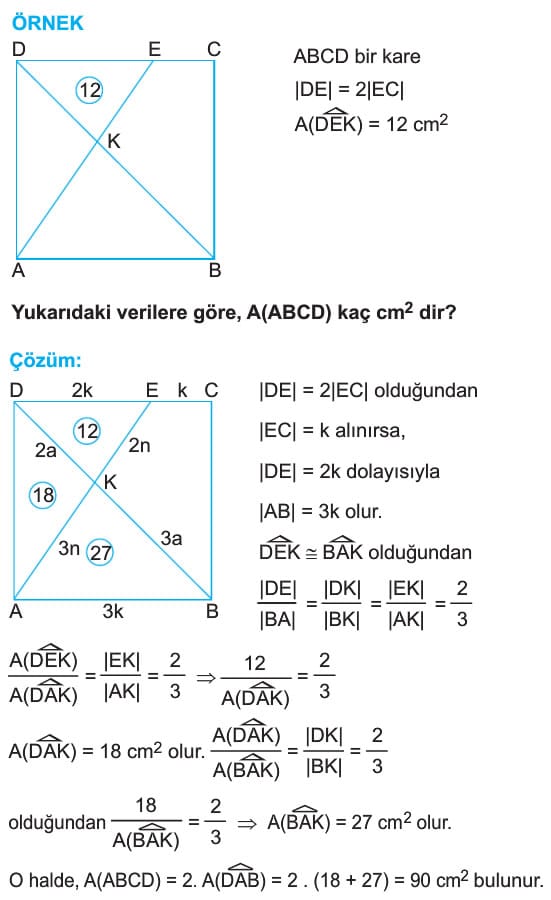
ÖRNEK: ABCD bir kare
[BD] köşegen
|DE| = 14 cm
|EB| = 2 cm
|AE| = x
Yukarıdaki verilere göre, x kaç cm dir?
Çözüm: [AC] köşegeni çizilirse
[AC] dik [BD] olur.
|BD| = 14 + 2 = 16 cm olduğundan
|DO| = |OB| = 8 cm dolayısıyla
|OE| = 6 cm dir.
Ayrıca |AC| = |BD| = 16 cm olduğundan
|AO| = |OC| = 8 cm dir. OAE dik üçgeninde pisagor teoremi uygulanırsa, |AE| = x = 10 cm bulunur.

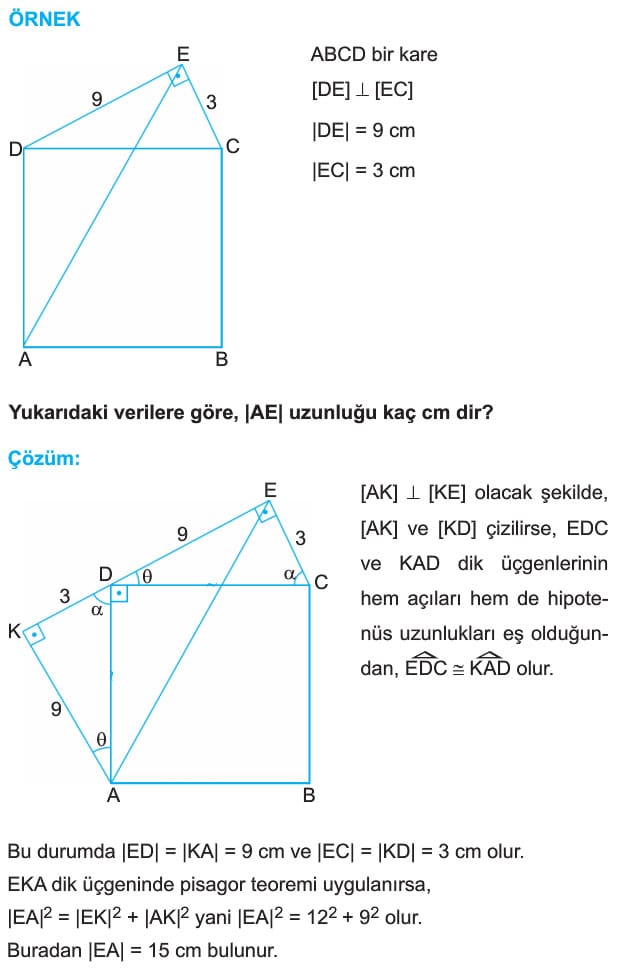
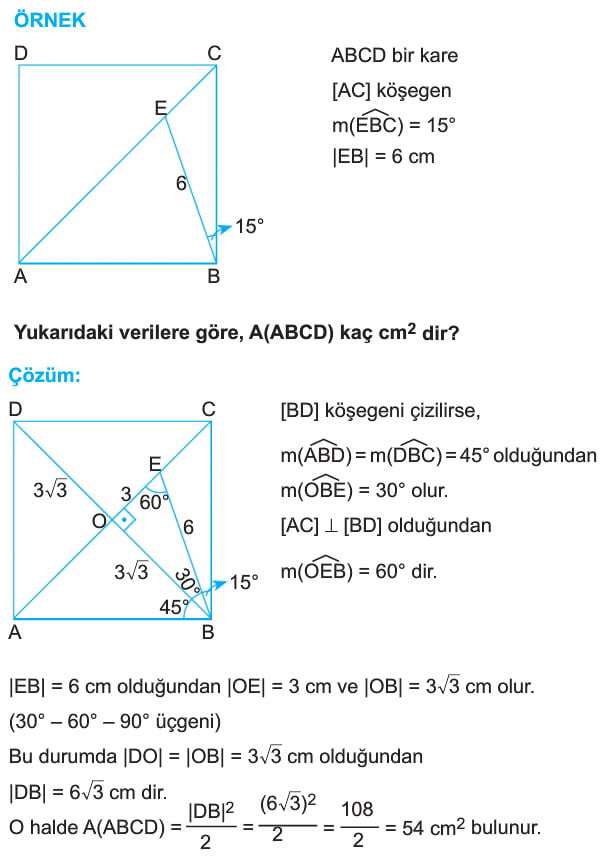
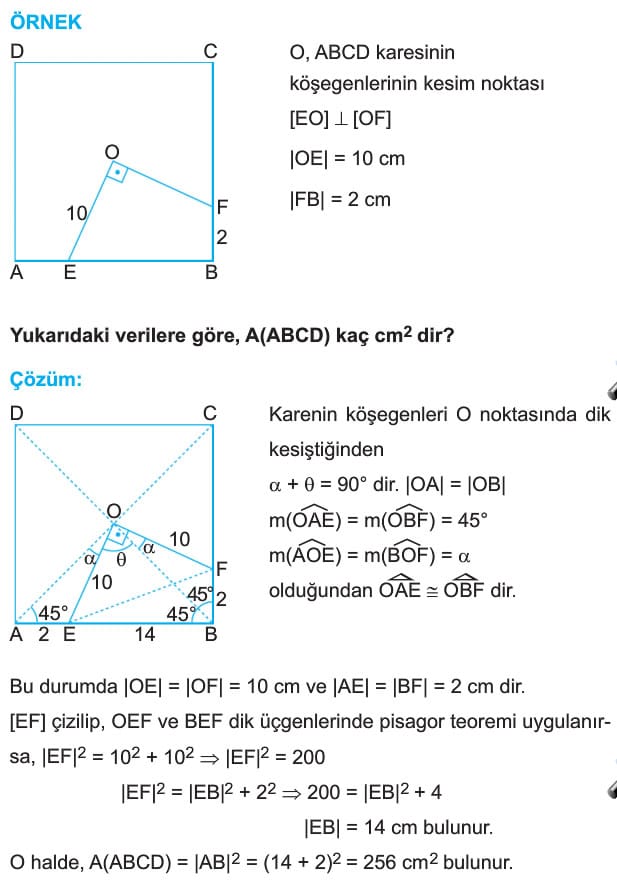
ÖRNEK: ABCD bir kare
[DE] dik [EC]
|DE| = 9 cm
|EC| = 3 cm
Yukarıdaki verilere göre, |AE| uzunluğu kaç cm dir?
Çözüm: [AK] dik [KE] olacak şekilde,
[AK] ve [KD] çizilirse, EDC ve KAD dik Üçgenlerinin hem açıları hem de hipotenüs uzunlukları eş olduğundan, EDC eştir KAD olur.
Bu durumda |ED| = |KA| = 9 cm ve |EC| = |KD| = 3 cm olur.
EKA dik üçgeninde pisagor teoremi uygulanırsa,
|EA|2 = |EK|2 + |AK|2 yani |EA|2 =122 + 92 olur.
Buradan |EA| = 15 cm bulunur.

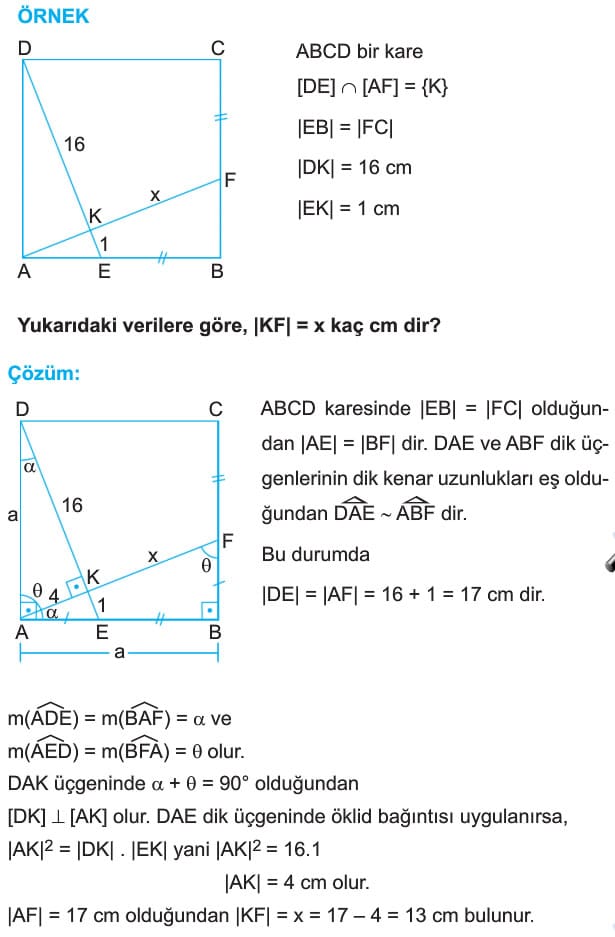
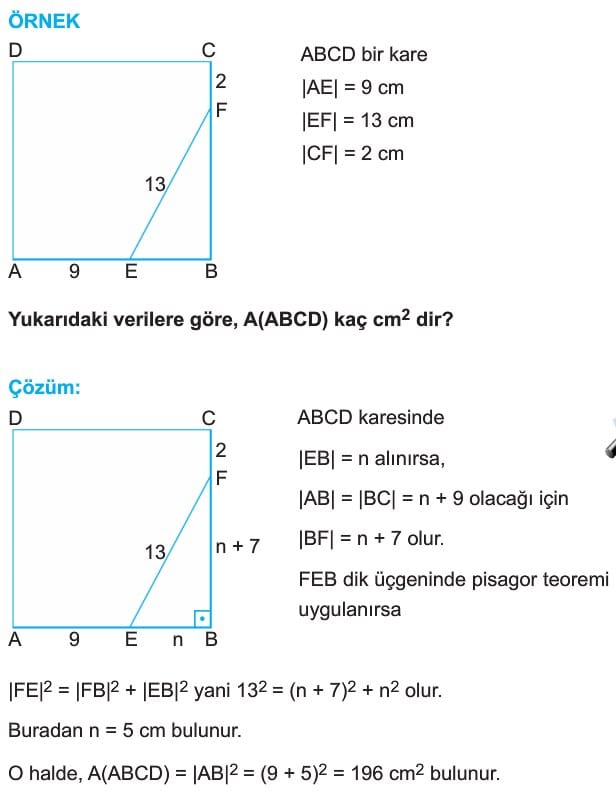
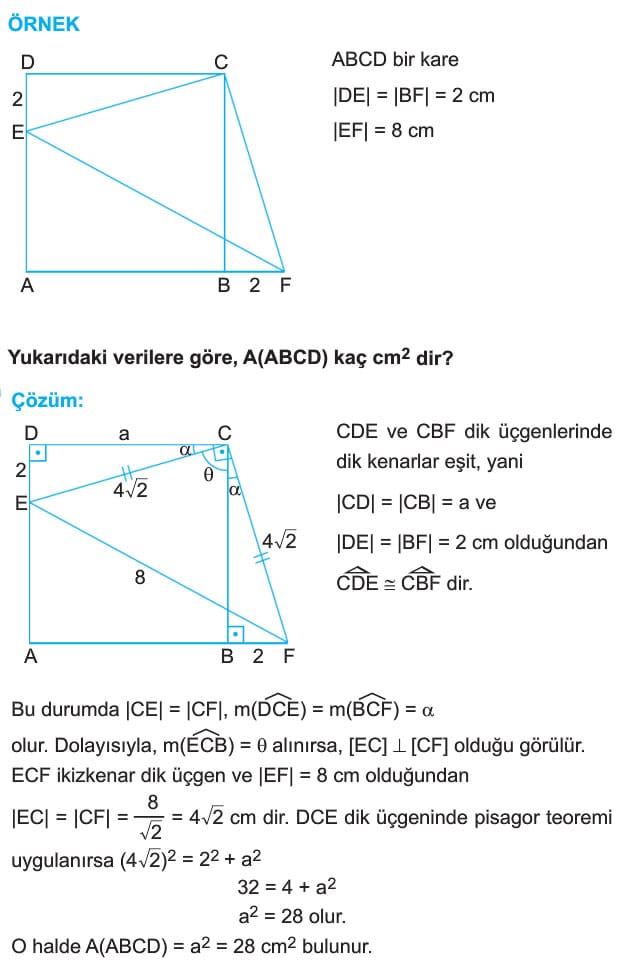
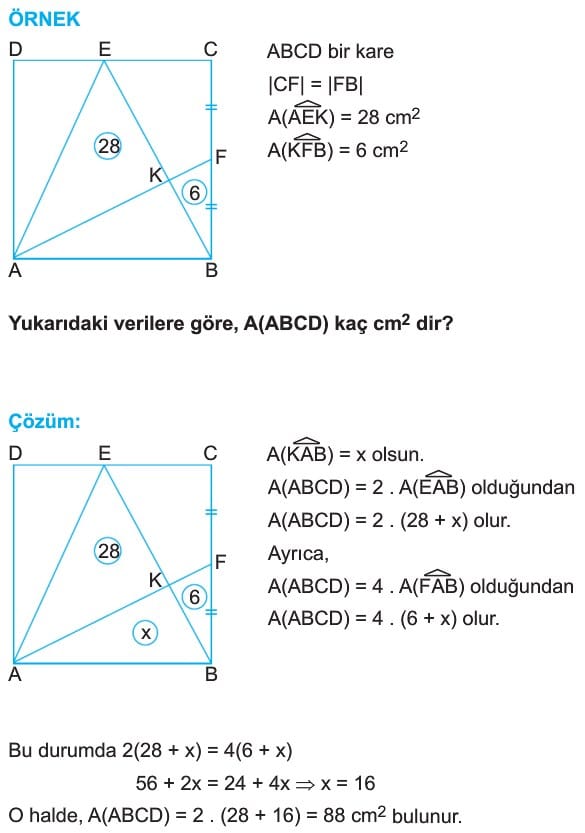
ÖRNEK: ABCD bir kare
|AE| = 9 cm
|EF| = 13 cm
|CF| = 2 cm
Yukarıdaki verilere göre, A(ABCD) kaç cm2 dir?
Çözüm: ABCD karesinde
|EB| = n alınırsa,
|AB| = |BC| = n + 9 olacağı için
|BF| = n + 7 olur.
FEB dik üçgeninde pisagor teoremi uygulanırsa
|FE|2 = |FB|2 + |EB|2 yani 132 = (n + 7)2 + n2 olur.
Buradan n = 5 cm bulunur.
O halde, A(ABCD) = |AB|2 = (9 + 5)2 = 196 cm2 bulunur.

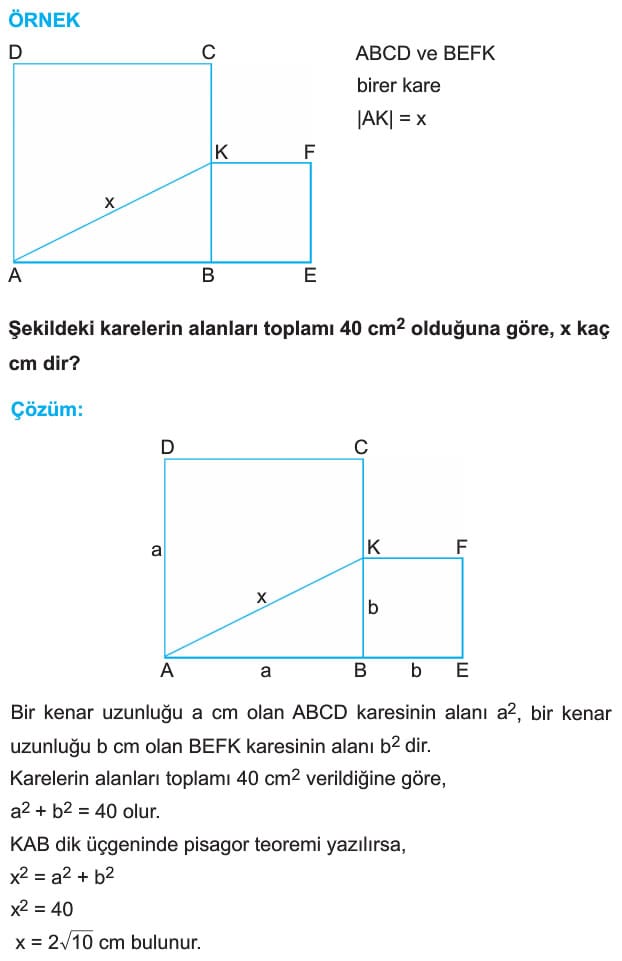
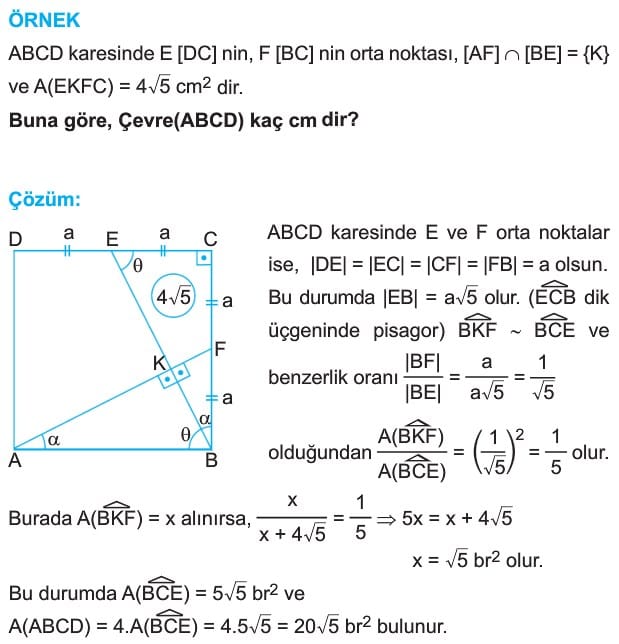
ÖRNEK: ABCD ve BEFK
birer kare
|AK| = x
Şekildeki karelerin alanları toplamı 40 cm2 olduğuna göre, x kaç cm dir?
Çözüm: Bir kenar uzunluğu a cm olan ABCD karesinin alanı az, bir kenar uzunluğu b cm olan BEFK karesinin alanı b2 dir.
Karelerin alanları toplamı 40 cm2 verildiğine göre,
a2 + b2 = 40 olur.
KAB dik üçgeninde pisagor teoremi yazılırsa,
x2 = a2 + b2
x2 = 40
x = 2√10 cm bulunur.

Kare konusu 11. sınıf geometri dersinin bir konusudur ve ösym'nin yaptığı ygs, lys, kpss gibi matematik sınavlarında soru gelmektedir. Kare konu anlatımı videosunun içeriğinde aşağıdaki başlıklar anlatılmaktadır.

  • Kare nedir, tanımı
  • Karenin alanı ve çevresi ile ilgili bağıntılar
  • Karenin kenarları, açıları ve köşegenleri ile ilgili genel özellikleri
  • Kare ile ilgili örnek soru çözümleri