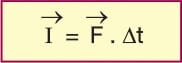İtme ve Çizgisel Momentum Fizik Ayt
İTME VE ÇİZGİSEL MOMENTUM
İtme:
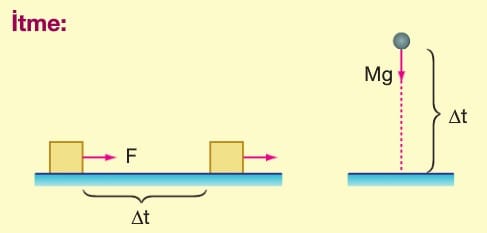
Sürtünmesiz bir ortamda yatay bir F kuvvetinin etkisinde Δt süresi boyunca hareket eden bir cisim ve yerçekimi etkisi ile Δt süresi boyunca düşen bir başka cisim düşünelim;
Her ikiside Δt süresi boyunca bir kuvvetin etkisi altında hareket etmektedir. Bu şekilde, “Bir cisme hareketi doğrultusunda etki eden net kuvvet ile kuvvetin etki ettiği sürenin çarpımına itme denir.
İtme vektörel bir büyüklüktür ve I harfi ile gösterilir.
Kuvvetin birimi Newton ve etki etme süresi saniye alındığından, itmenin birimi N.s olur.
Momentum:
Bir cismin kütlesi ile çizgisel hızının çarpımına çizgisel momentum denir.
Çizgisel momentum P harfi ile gösterilir.
Kütle kg ve hız m/s alındığında momentum birimi kg m/s olur.
700 m/s hızla hareket eden 10 kg ağırlığındaki bir top mermisinin momentumu ile 10 m/s hızla hareket eden 700 kg kütleli bir arabanın momentumunu karşılaştırınız.
Bu örnekten anlaşılacağı üzere, küçük kütleli cisimler yüksek hızlarından dolayı büyük momentum değerlerine sahip olabilirler.
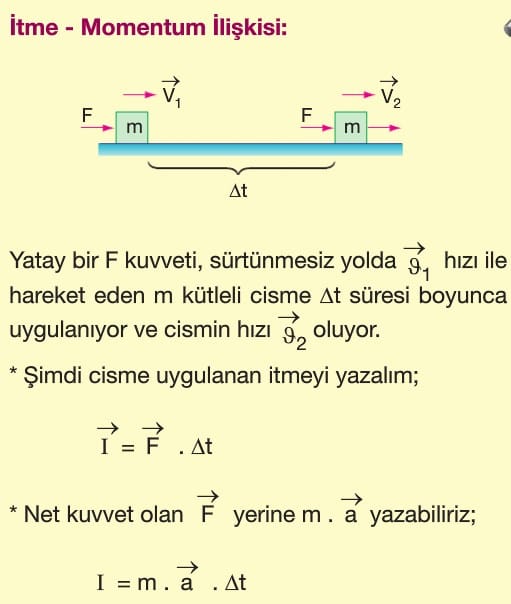
Yani, bir cisme uygulanan itme, cismin momentum değişimine eşittir.
Şimdi ise konuyla ilgili grafiklere göz atalım;
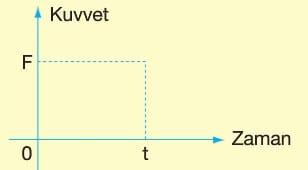
* Kuvvet—zaman grafiği
Grafik parçasının altındaki alan F.Δt olarak bulunur. Yani, kuvvet—zaman grafiğinin altındaki alan itmeyi (I) ve momentum değişimini (ΔP) verir.
Momentum-Zaman Grafiği:
Grafiğin eğimini incelersek;
Momentum-Kinetik Enerji İlişkisi:
Kinetik enerji formülü üzerinde biraz oynayalım,
Momentum Korunumu:
Bir cismin yada sistemin momentumu dışarıdan bir kuvvet etki etmedikçe değişmez sabit kalır. Buna Momentum Korunumu adı verilir.
Newton hareket kanunlarının birincisini yani eylemsizlik prensibini hatırlarsak, buradan momentum korunumuna geçiş yapabiliriz. Bir cisim üzerine etki eden net kuvvet sıfır ise, cisim ya duruyordur, yada sabit hızla yoluna devam ediyordur. Yani her iki durumda da cismin hızında dolayısıyla momentumunda bir değişim olmaz. (Cismin kütlesininde değişmediğini varsayıyoruz.)
Momentumun korunumunu çarpışmalar, patlamalar gibi etkileşimlerde inceleyeceğiz.
Çarpışmalar:
Çarpışmalar momentumun ve kinetik enerjinin korunup korunmamasına göre esnek çarpışma ve esnek olmayan çarpışma olarak iki ana başlık altında incelenir.
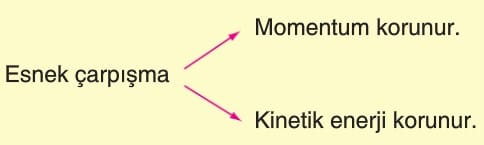
1. Esnek Çarpışma:
Hern momentumun hemde kinetik enerjinin korunduğu çarpışmalara denir. Kendi içinde merkezi esnek çarpışma ve merkezi olmayan esnek çarpışma olarak ikiye ayrılır.
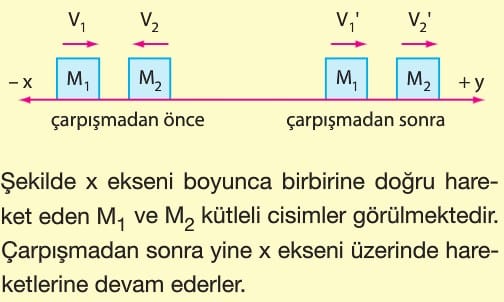
a) Merkezi Esnek Çarpışma
Aynı doğrultuda hareket eden cisimlerin çarpışmasıdır. Cisimler çarpışmadan sonrada aynı hareket doğrultusunda kalırlar ve birbirlerinden ayrılırlar. Yani birbirlerine yapışıp beraber hareket etmezler.
Merkezi Esnek Çarpışmada Özel Durumlar;
* Eşit kütleli cisimlerin çarpışması
* Eşit kütleli momentum büyüklüğüne sahip cisimlerin çarpışması
Bu iki özel durumu örnek 3 ve örnek 4’te incelenerek sonuçlar çıkarılmıştır.
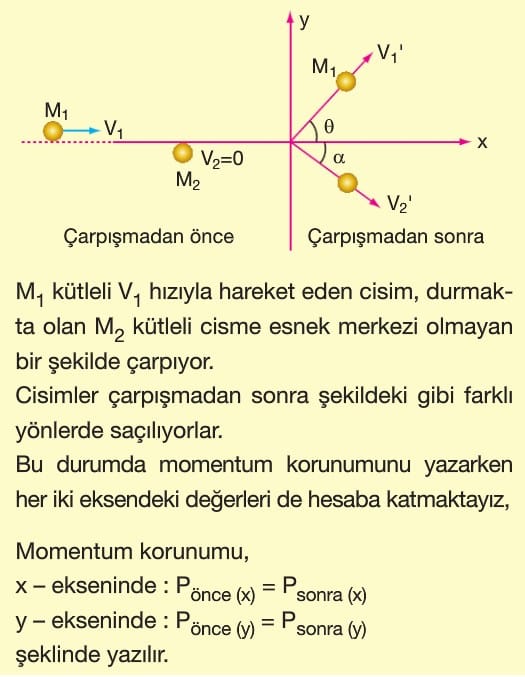
b) Merkezi Olmayan Esnek Çarpışma
Cisimlerin çarpışmadan önce ve sonra farklı doğrultularda hareket ettiği çarpışmalardır.
Bu çarpışmada da momentum ve kinetik enerji korunur.
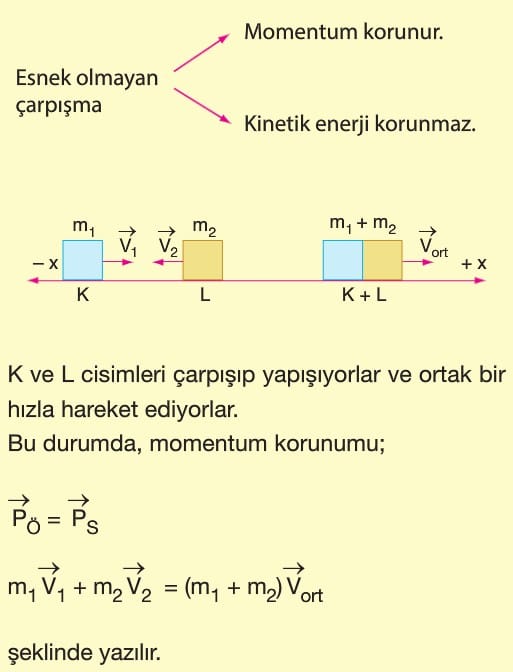
2. Esnek Olmayan Çarpışma:
Momentumun korunduğu, kinetik enerjinin korunmadığı çarpışmalardır. Bu çarpışmalarda çisimler genellikle çarpışma sonrası yapışarak beraber hareket ederler.
Patlamalar
Patlama olayı herhangi bir dış kuvet etkisi olmaksızın, iç kuvvetlerin etkisi ile cisimlerin parçalanıp dağılması şeklinde gerçekleşir.
Patlamadan önce bütün halindeki parçanın momentumu, patlama ile oluşan parçaların momentum vektörlerinin toplamına eşittir.