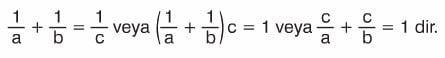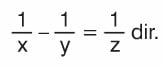İşçi havuz problemleri konu anlatımı çözümlü sorular ders notu 9. sınıf matematik Ygs

İşçi ve havuz problemlerinde birim zamanda yapılan iş üzerinden işlem yapılır.
Örneğin; bir işçi bir işi a günde, ikinci işçi b günde ve ikisi birlikte x günde yapıyorlarsa, 1/a + 1/b = 1 / x bağıntısı yazılır.
Örneğin;  Bir işi A işçisi x günde, B işçisi y günde, C işçisi z günde bitiriyor. Üç işçi birlikte k gün çalıştıktan sonra C işçisi işi bırakırsa kalan işi A ve B işçileri p günde bitirirse bunun kuralı, k . (1/x + 1/ y + 1 / z) + p . (1 / x + 1 / y) = 1 şeklindedir.
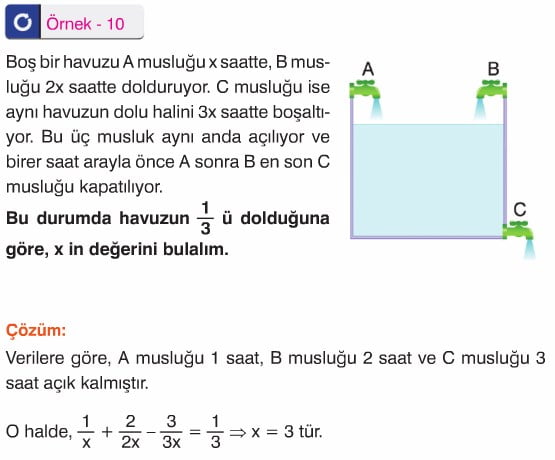
Havuz problemleri de işçi problemleri gibi yorumlanarak çözülür.
Örneğin; birinci musluk bir havuzu a saatte dolduruyor, ikinci musluk b saatte boşaltıyor ve ikisi birlikte x saatte dolduruyorsa, 1/a - 1/b = 1 / x
Mehmet bir işi tek başına 30 günde, Ahmet aynı işi tek başına 60 günde bitirebilmektedir. Birlikte çalıştıklarında bu işin tamamını kaç günde bitirebileceklerini bulalım.
Örnek: Bir işi İlknur 12 günde, Cemile ise 20 günde bitirebilmektedir. İkisi birlikte işe başlayıp 3 gün çalıştıktan sonra İlknur işten ayrılıyor. Geriye kalan işi Cemile'nin tek başına kaç günde bitirebileceğini bulalım.
Örnek: Aynı kapasitede 7 işçi beraberce bir işi yapmaya başlıyorlar. Her günün sonunda işçilerden biri işi bırakıyor.
Bu şekilde iş 3 günde bittiğine göre, işçilerden ikisinin işin tamamını kaç günde bitirebileceğini bulalım.
Örnek: Bir elbiseyi eş güçte 3 usta 8 günde, eş güçte 6 çırak 15 günde dikebiliyor. Buna göre, bu usta ve çıraklarla eş güçte 4 usta ve 3 çırağın birlikte çalışarak aynı elbiseyi kaç günde dikebileceğini bulalım.
Örnek: Boş bir havuzu A ve B muslukları birlikte 15 saatte dodurabilmektedir. A musluğu tek başına 8 saat şu akıttıktan sonra B musluğu açılıyor. Birlikte havuzun kalan kısmını 10 saatte doldurduklarına göre, B musluğunun havuzun tamamını tek başına kaç saatte doldurabildiğini bulalım.