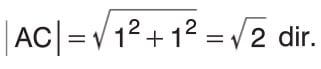Herhangi iki rasyonel sayı arasında sonsuz sayıda rasyonel sayı bulunabilmesine karşılık sayı doğrusu üzerindeki her bir nokta bir rasyonel sayı ile gösterilemez. Örneğin; “Bir kenarı 1 birim olan bir karenin köşegen uzunluğu iki tam sayının oranı şeklinde yazılamaz.”

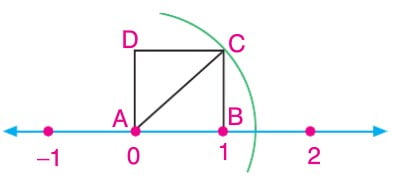
Aşağıdaki şekli inceleyelim.

Şekilde karenin köşegen uzunluğu Pisagor teoreminden

kök 2 birim uzunluğu olan |AC| köşegeni sayı doğrusu üzerinde 1 ile 2 arasında bir noktaya karşılık gelir. Bu noktaya karşılık gelen kök 2 değeri iki tam sayının oranı biçiminde yazılamaz. Bu tür sayılara irrasyonel sayılar adını veriyoruz.

İki tam sayının oranı (a / b, b ≠ 0) biçiminde yazılamayan sayılara irrasyonel sayılar denir ve Q’ sembolü ile gösterilir. İrrasyonel sayılar, ondalık açılımı sınırsız ve tekrarsız olan sayılardır. Aşağıda irrasyonel sayılara bazı örnekler verilmiştir.

İrrasyonel sayılar ondalık gösterimle ifade edilemez, çünkü bu sayıların ondalık kısımları herhangi bir tekrarlama olmaksızın sonsuza kadar devam etmektedir.

Hem rasyonel hem de irrasyonel olan sayı yoktur. Diğer bir ifadeyle, rasyonel sayılar kümesi ile irrasyonel sayılar kümesinin kesişimi boş kümedir.
Yani, Q ∩ Q’ = Ø  dir.