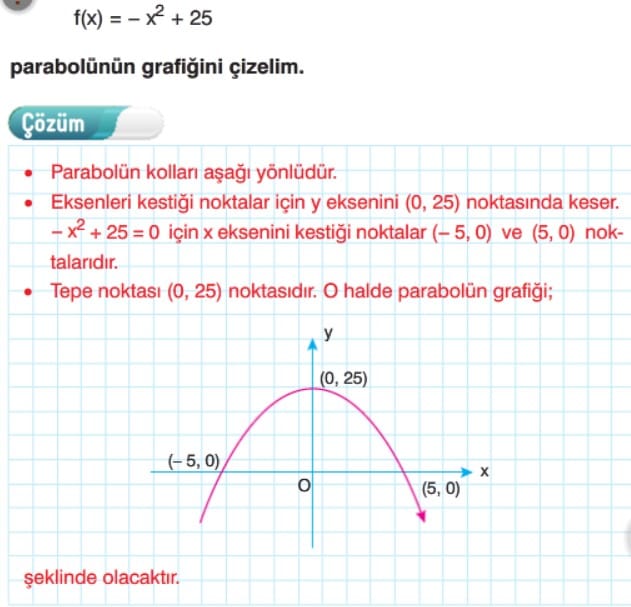
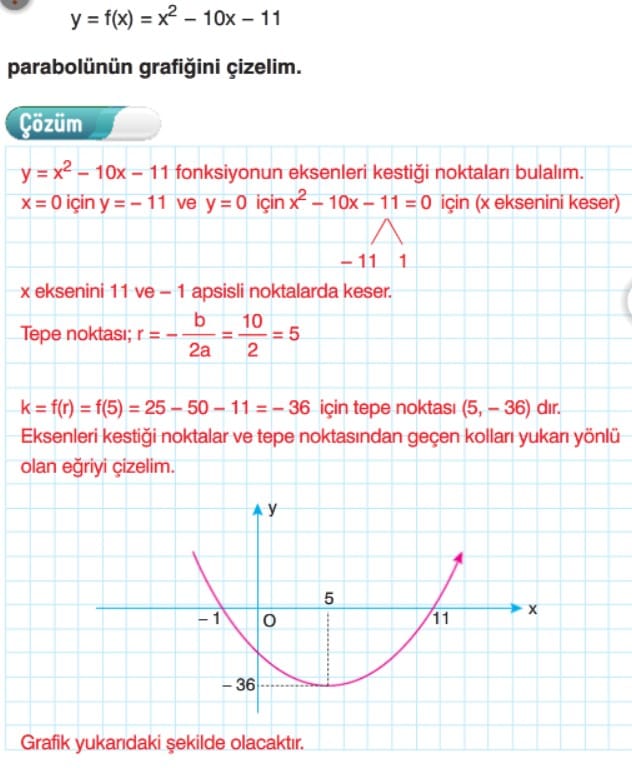
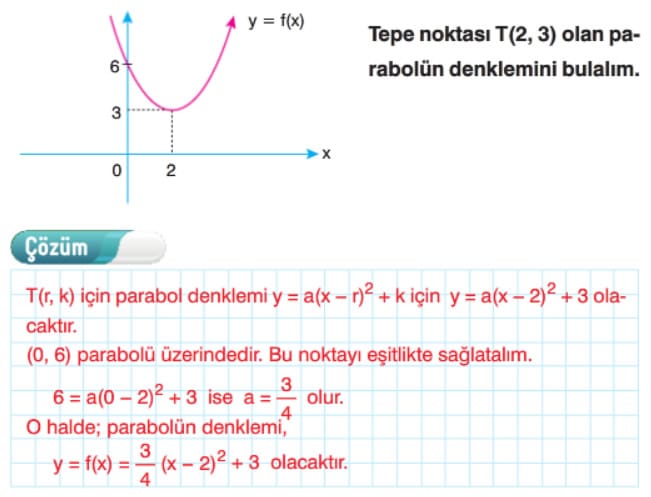
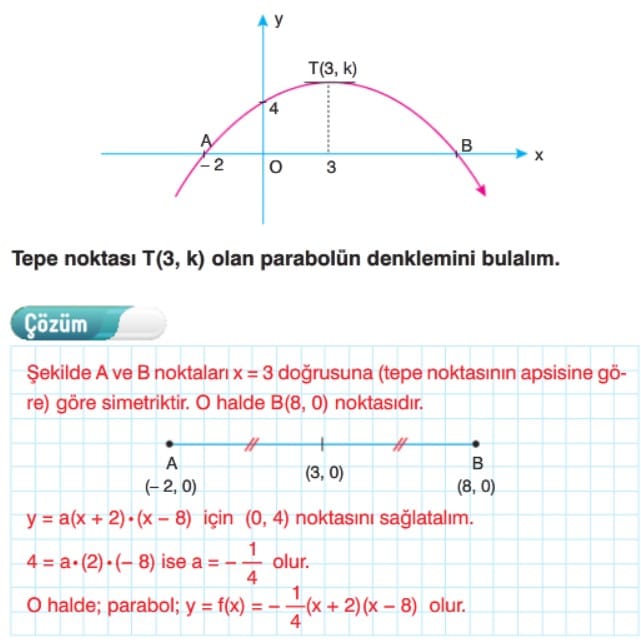
İkinci Dereceden Fonksiyonların Grafikleri (Parabol) 11. Sınıf
İkinci Dereceden Bir Bilinmeyenli Fonksiyonlar (Parabol)




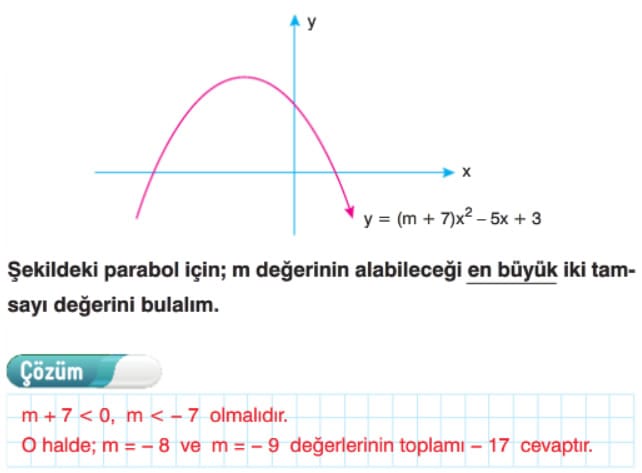
Çözümlü Sorular
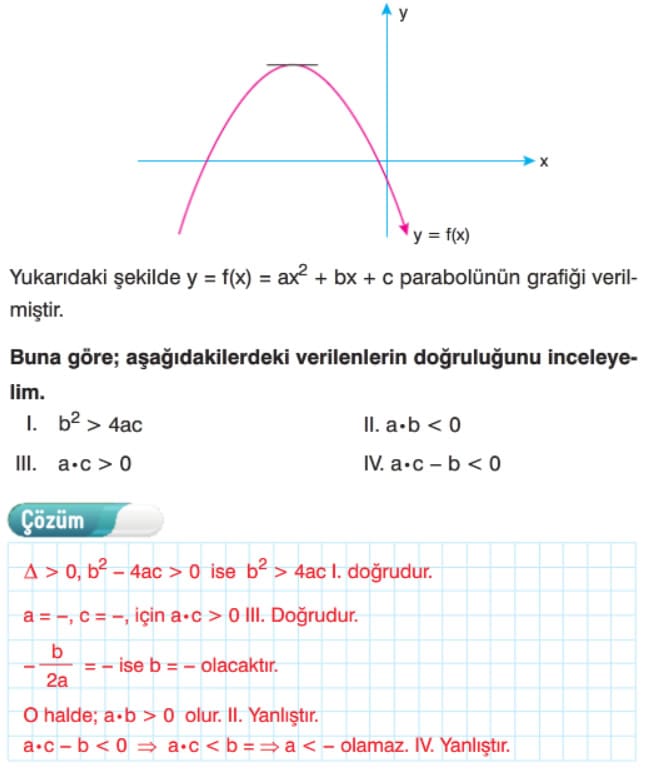
f(x) = ax2 + bx + c, Parabolünün Katsayılarının İncelenmesi ve Parabolün Eksenleri Kestiği Noktalar



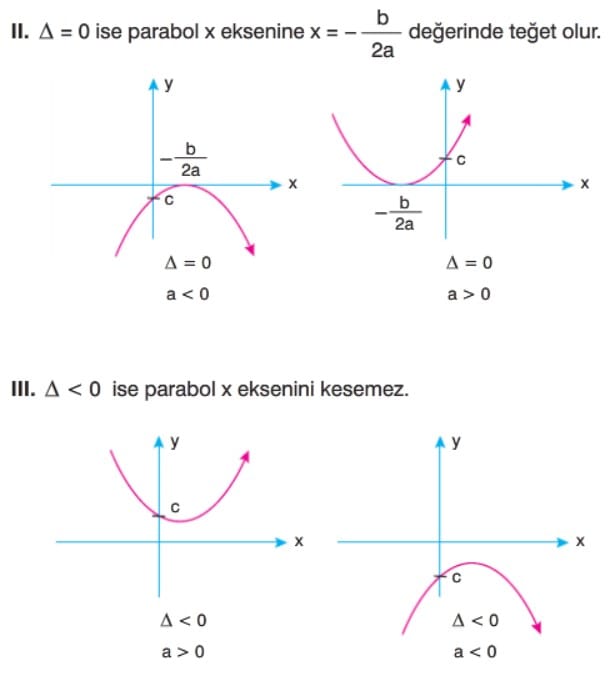

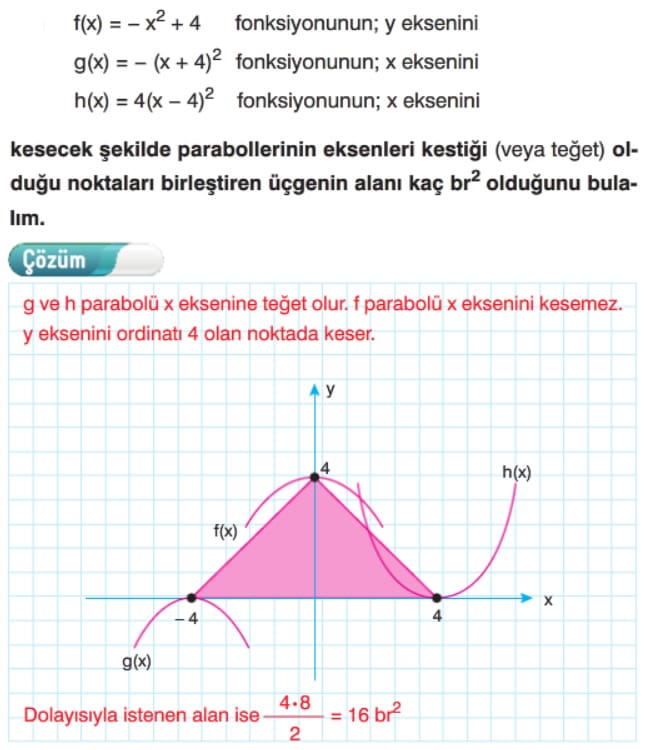
Çözümlü Sorular
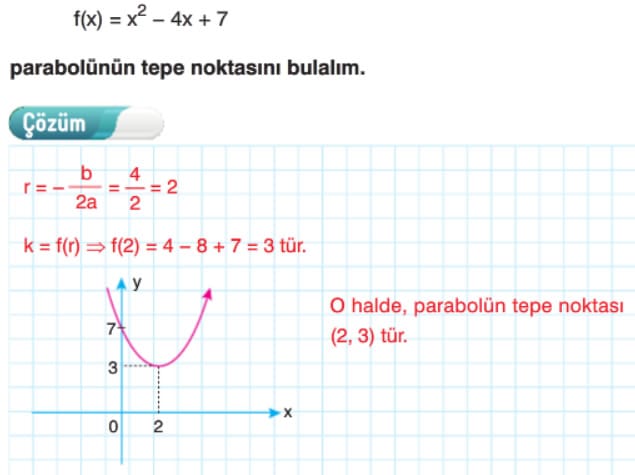
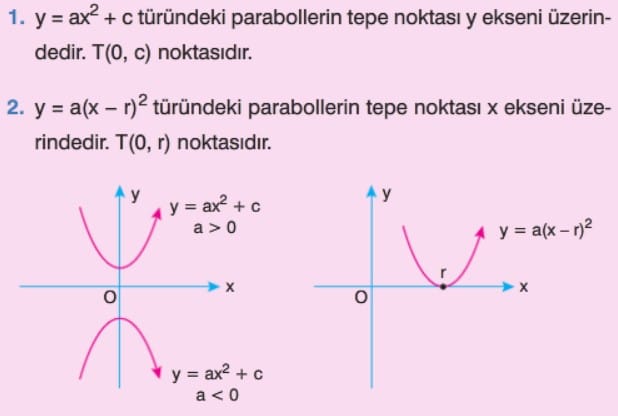
Parabolün Tepe Noktası
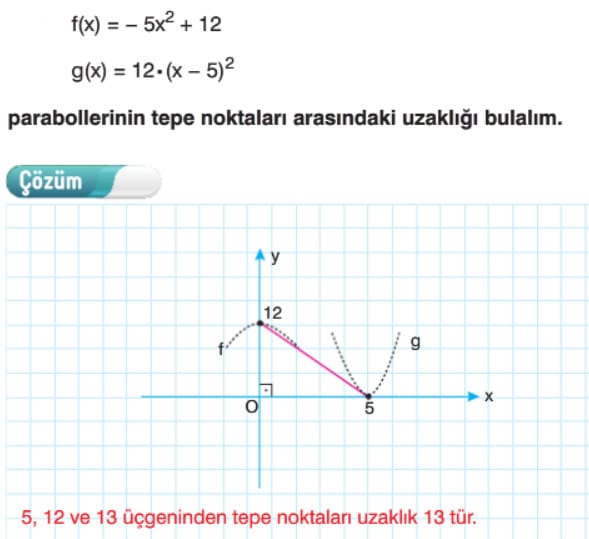
Çözümlü Sorular
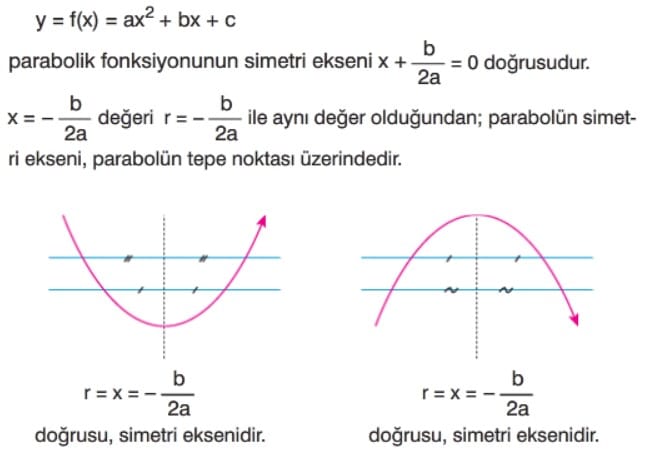
Parabolün Simetri Ekseni
Çözümlü Sorular
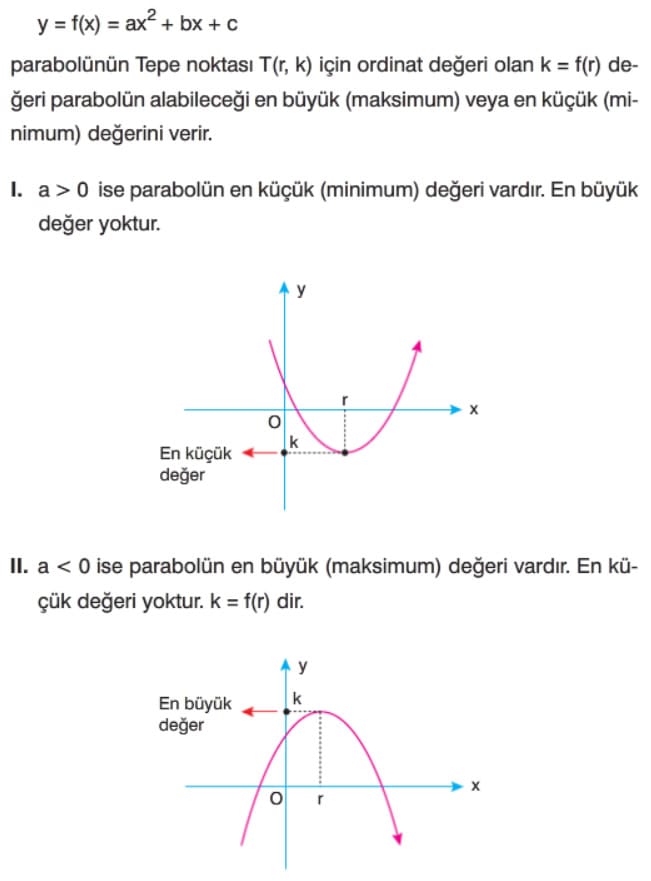
Parabolün En Küçük ve En Büyük Değeri

Parabolün En Küçük ve En Büyük Değeri Çözümlü Sorular
Parabol Çizimi


Parabolün Çizimi Çözümlü Sorular
Parabolün Denklemini Kurma

Parabolün Denklemini Kurma Çözümlü Sorular
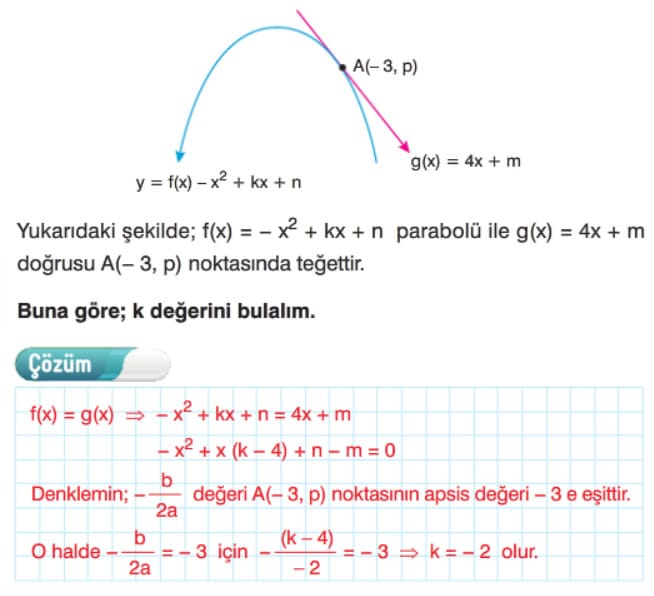
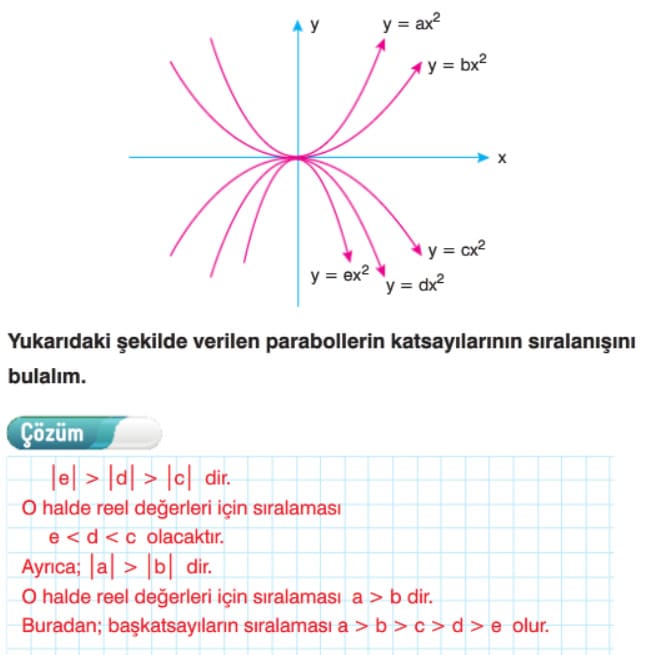
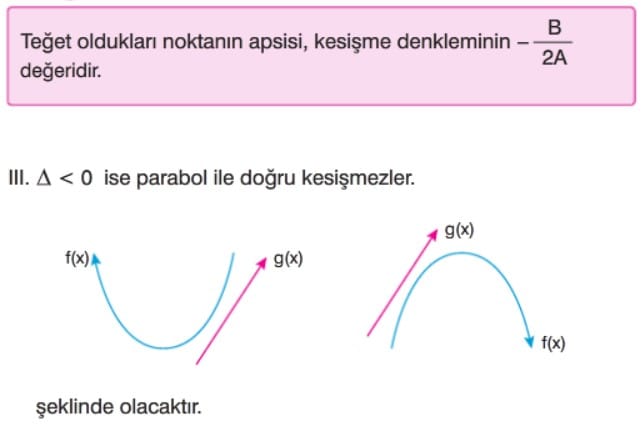
Doğru İle Parabol İlişkisi (Doğru İle Parabolün Kesişme Durumları)


Doğru İle Parabol İlişkisi Çözümlü Sorular
Çözümlü Örnek Test Soruları
Soru 1:
f(x) = x² – 4x + 3 fonksiyonunun grafiğinin tepe noktası nedir?
A) (1, 4)
B) (2, -1)
C) (3, -4)
D) (2, 1)
E) (1, -3)
Çözüm:
Tepe noktasının x-koordinatı, x = -b / 2a formülü ile bulunur.
Burada a = 1 ve b = -4 olduğuna göre:
x = -(-4) / 2(1) = 4 / 2 = 2
x = 2 için f(2) değerini bulalım:
f(2) = (2)² – 4(2) + 3 = 4 – 8 + 3 = -1
Tepe noktası (2, -1) olur.
Cevap: B
Soru 2:
f(x) = -2x² + 8x – 5 parabolünün kolları yukarı mı yoksa aşağı mı bakar? Tepe noktasının koordinatlarını bulunuz.
A) Yukarı, (2, 3)
B) Aşağı, (2, 3)
C) Yukarı, (3, 2)
D) Aşağı, (3, 2)
E) Aşağı, (2, -3)
Çözüm:
a = -2 olduğuna göre, parabolün kolları aşağıya bakar.
Tepe noktasının x-koordinatı, x = -b / 2a formülü ile bulunur.
x = -8 / 2(-2) = 8 / 4 = 2
x = 2 için f(2) değerini bulalım:
f(2) = -2(2)² + 8(2) – 5 = -8 + 16 – 5 = 3
Tepe noktası (2, 3) olur.
Cevap: B
Soru 3:
f(x) = x² + 6x + 5 fonksiyonunun grafiği x-eksenini hangi noktalarda keser?
A) (-5, 0) ve (1, 0)
B) (-3, 0) ve (-2, 0)
C) (0, 5) ve (5, 0)
D) (-4, 0) ve (3, 0)
E) (1, 0) ve (5, 0)
Çözüm:
Parabolün x-eksenini kestiği noktalar, f(x) = 0 eşitliğinden bulunur.
x² + 6x + 5 = 0
Bu denklemi çarpanlarına ayırırsak:
(x + 5)(x + 1) = 0
x = -5 ve x = -1
Dolayısıyla, x-eksenini (-5, 0) ve (-1, 0) noktalarında keser.
Cevap: A
Soru 4:
Bir parabol f(x) = x² – 2x + 1 şeklinde tanımlanıyor. Bu parabolün tepe noktası nedir?
A) (1, 0)
B) (2, 1)
C) (0, 1)
D) (-1, 0)
E) (1, 1)
Çözüm:
Tepe noktasının x-koordinatı, x = -b / 2a formülü ile bulunur.
Burada a = 1 ve b = -2 olduğuna göre:
x = -(-2) / 2(1) = 2 / 2 = 1
x = 1 için f(1) değerini bulalım:
f(1) = (1)² – 2(1) + 1 = 1 – 2 + 1 = 0
Tepe noktası (1, 0) olur.
Cevap: A
Soru 5:
f(x) = -x² + 4x + 6 fonksiyonunun grafiği, tepe noktasının x-koordinatında maksimum değeri alır. Bu maksimum değeri bulunuz.
A) 8
B) 10
C) 12
D) 14
E) 16
Çözüm:
Tepe noktasının x-koordinatı, x = -b / 2a formülü ile bulunur.
Burada a = -1 ve b = 4 olduğuna göre:
x = -4 / 2(-1) = 4 / 2 = 2
x = 2 için f(2) değerini bulalım:
f(2) = -(2)² + 4(2) + 6 = -4 + 8 + 6 = 10
Maksimum değer 10’dur.
Cevap: B
Soru 6:
f(x) = 3x² – 6x + 2 fonksiyonunun grafiğinin tepe noktasının koordinatlarını bulunuz.
A) (1, -1)
B) (2, 3)
C) (-1, 4)
D) (0, 2)
E) (3, -2)
Çözüm:
Tepe noktasının x-koordinatı, x = -b / 2a formülü ile bulunur.
Burada a = 3 ve b = -6 olduğuna göre:
x = -(-6) / 2(3) = 6 / 6 = 1
x = 1 için f(1) değerini bulalım:
f(1) = 3(1)² – 6(1) + 2 = 3 – 6 + 2 = -1
Tepe noktası (1, -1) olur.
Cevap: A
İkinci Dereceden Bir Değişkenli Fonksiyonlar
a, b, c ∈ R ve a ≠ 0 olmak üzere f: R→R, y=f(x)=ax2 + bx + c biçimindeki fonksiyonlara ikinci dereceden bir değişkenli fonksiyon denir. Fonksiyonun analitik düzlemdeki grafiği olan eğriye parabol denir.
Bilgi: Bir fonksiyonun grafiğinin x eksenini kestiği noktaları bulmak için fonksiyonda y = f(x) değeri sıfıra eşitlenir. Fonksiyonun grafiğinin y eksenini kestiği noktayı bulmak için fonksiyonda x değerine sıfır verilir.
Bilgi: Bir fonksiyonun grafiği üzerinde bulunan her nokta fonksiyonun denklemini sağlar.
Parabolün En Büyük ve En Küçük Değeri
f(x) = ax2 + bx + c parabolünde
- a > 0 ise parabolün alabileceği en küçük değer parabolün tepe noktasının ordinatıdır.
- a < 0 ise parabolün alabileceği en büyük değer tepe noktasının ordinatıdır.
- Bu durum parabolün herhangi bir aralıktaki parçası için geçerli değildir.
[a, b] aralığındaki parabolün maksimum-minimum değeri sorulursa tepe noktası T(r, k) olmak üzere f(r), f(a) ve f(b) ye bakılır.
Tepe Noktası ve Bir Noktası Bilinen Parabol Denklemi
T(r, k) parabolün tepe noktası ve A(x0, y0) parabol üzerinde bir nokta ise parabolün denklemini bulmak için
y = a.(x – r)2 + k
yazıldıktan sonra a değerini bulmak için verilen nokta yerleştirilir.
x Eksenin Kestiği Noktalar ve Üzerindeki Başka Bir Noktası Bilinen Parabolün Denklemi
f(x) parabolünün x eksenini kestiği noktalar A(x1, 0) ve B(x2, 0) ise parabolün denklemi
f(x) = a. (x – x1) . (x – x2) biçiminde yazılır. Bilinmeyen a değerini bulmak için parabolün üzerindeki nokta denklemde yazılır.
Üç Noktası Bilinen Parabol Denklemi
A(x0, y0) , B(x1, y1) ve C(x2, y2) noktaları parabolün üzerinde ise üçü de parabolün denklemini sağlar. Bu noktalar parabolün genel denklemi olan y=f(x) =ax2 + bx + c de yerleştirilirse üç bilinmeyenleri üç denklem çözülür a, b, c değerleri bulunur.
Bir Doğru İle Bir Parabolün Birbirlerine Göre Durumları
y = ax2 + bx + c parabolü ile y = mx + n doğrusunun denklemleri birbirine eşitlenip oluşan denklemin diskriminantına bakılır. (Δ = b2 – 4ac)
- Δ > 0 ise parabol ve doğru iki noktada kesişir.
- Δ = 0 ise parabol doğruya teğet-tir.
- Δ < 0 ise parabolle doğru kesişmez.
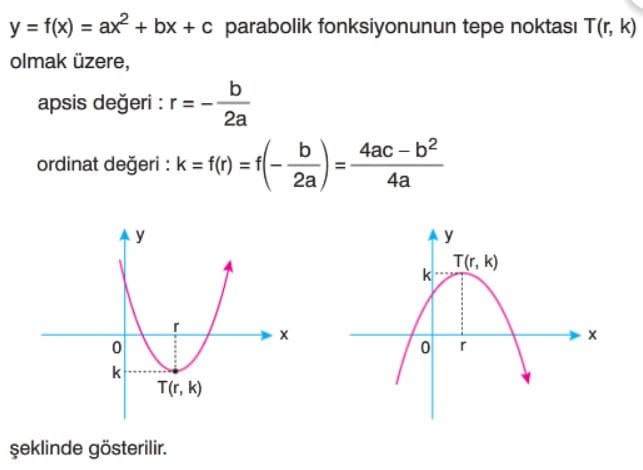
Bilgi: y = f(x) = ax2 + bx + c parabolünün x eksenini kesip kesmediğini yorumlamak için x ekseni y = 0 doğrusu olduğundan ax2 + bx + c = 0 denkleminin diskriminantına bakılır.
- Δ > 0 ise parabol x eksenini iki farklı noktada keser.
- Δ = 0 ise parabol x eksenine teğet-tir.
- Δ < 0 ise parabol x eksenini kesmez.
Parabol (İkinci Dereceden Fonksiyonlar) konusu 10. sınıf matematik müfredatında yer almakta olup lys matematik sınavında soru çıkmaktadır.
Parabol (İkinci Dereceden Fonksiyonlar) konu başlıkları:
- y = f(x) = ax^2 Fonksiyonunun Grafiği
- y = f(x) = ax^2 + c Fonksiyonunun Grafiği
- y = f(x) = ax^2 + b.x + c Fonksiyonunun Grafiği
- y = a. (x – r)^2 + k Fonksiyonunun Grafiği
- Grafiği Verilen Bir Parabolün Denklemini Bulma
- Bir Parabol ile Doğrunun Durumu
- İki bilinmeyenli eşitsizliklerin grafik ile çözümü
Parabol, ikinci dereceden bir matematiksel fonksiyondur ve genellikle şu formülle ifade edilir:
f(x) = ax2 + bx + c
Bu formülde a, b ve c sabitlerdir ve a sıfırdan farklı bir sayı olmalıdır. Parabol, genellikle bir “U” şeklinde bir eğri olarak tanımlanır.
Parabolün tepe noktası, eğer a pozitifse parabolün en yüksek noktasıdır. Eğer a negatifse, parabolün en düşük noktasıdır. Tepe noktasının x ve y koordinatları, parabol fonksiyonunun tepe noktasını temsil eder.
Parabol, x-ekseni ile y-ekseni arasında bir simetriye sahiptir. Dolayısıyla, parabol eksenleri kestiği noktalar simetrik olacaktır. Eksenlerden biri genellikle parabolün tepe noktasından geçer. Bu eksenler, parabol fonksiyonunun sıfır olduğu noktalardır.
Parabol fonksiyonunun x-ekseniyle kestiği noktalar, genellikle “kök” veya “x-kesişim noktaları” olarak adlandırılır. Bu noktalar, parabolün grafiği x-ekseniyle kesiştiği noktalardır ve bu noktalarda f(x) = 0 olur. Parabol fonksiyonu genellikle iki gerçek köke sahiptir, ancak diskriminantın (b²-4ac) değerine bağlı olarak bu kök sayısı değişebilir.