2. dereceden denklemler 10. Sınıf
İkinci Dereceden Bir Bilinmeyenli Denklemler
a, b, c ∈ R ve a ≠ 0 olmak üzere,
ax2 + bx + c = 0
şeklindeki eşitliklere ikinci dereceden bir bilinmeyenli denklem denir.
- Denklemi sağlayan x gerçek (reel) sayılarına denklemin kökleri denir.
- Köklerin oluşturduğu kümeye çözüm kümesi (doğruluk kümesi) denir.
- Kökler denklemi sağlar.
Çözümlü Sorular
Çarpanlara Ayırma Yöntemi İle Kök Bulma


Çözümlü Sorular
Δ (Delta) ile Kök Bulma

Çözümlü Sorular
Karmaşık Sayılar
Karmaşık Sayı Tanımı
- ax2 + bx + c = 0 denkleminin Δ < 0 iken reel (gerçek) kökünün olmadığını daha önceden biliyoruz.
Örneğin x2 + 1 = 0 denkleminin reel kökü yoktur.
Çünkü x2 + 1 = 0 ise x2 = -1 dir. Karesi -1 olan reel sayı yoktur. - Şimdi bu türden denklemlerin çözümünü mümkün kılan ve reel sayılar kümesini de kapsayan yeni bir küme tanımlayacağız.
a ve b reel sayı, i2 = -1 olmak üzere
z = a + bi şeklinde ifade edilen z sayısına karmaşık (kompleks) sayı denir. Karmaşık sayılar kümesi C ile gösterilir.
C = {z: z = a+bi; a,b ∈ R ve i2 =-1} dir. - z = a + bi şeklindeki yazılışına z karmaşık sayısının standart biçimi denir.
- z = a + bi karmaşık sayısında a ya reel kısım, b ye imajiner (sanal) kısım denir ve Re(z) = a, im(z) = b şeklinde gösterilir.
Aşağıdaki sayıları inceleyiniz.
z = 2 + 5i ise Re(z) = 2, im(z) = 3
z = 4i – 5 ise Re(z) = -5, im(z) = 4
z = 6i ise Re(z) = 0, im(z) = 6
z = 7 ise Re(z) = 7, im(z) = 0 dir.
Çözümlü Sorular
İki Karmaşık Sayının Eşitliği

Çözümlü Sorular
Bir Karmaşık Sayının Eşleniği

Çözümlü Sorular
Kökleri Karmaşık Olan Denklemler

Not: Reel katsayılı ikinci dereceden bir denklemin köklerinden biri a + b.i ise diğer kök bunun eşleniği olan a – b.i dir.
Çözümlü Sorular
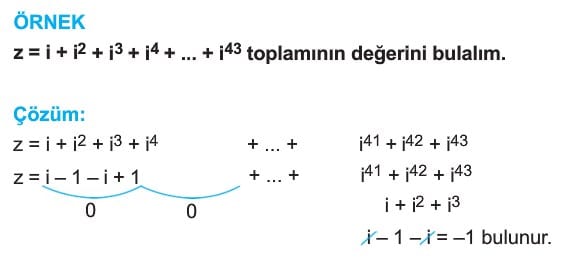
Karmaşık Sayılarda i nin Kuvvetleri (Fen Liseleri)

Çözümlü Sorular
Karmaşık Sayılarda Dört İşlem (Fen Liseleri)
Toplama ve Çıkarma İşlemi

Çarpma İşlemi


Bölme İşlemi

Çözümlü Sorular
Kökler ve Katsayılar Arasındaki İlişki

Simetrik Kök: ax2 + bx + c = 0 denkleminin simetrik iki kökü varsa b = 0 dır.
Simetrik kökler toplama işlemine göre birbirinin tersidir. (x1 = -x2)
Çözümlü Sorular
Kökleri Verilen İkinci Dereceden Denklemin Yazılması

Çözümlü Sorular
İkinci Dereceden Denklemler – 10. Sınıf Konu Anlatımı ve Çözümlü Sorular
Konu Anlatımı
İkinci dereceden denklemler, en genel haliyle şu şekilde yazılır:
ax² + bx + c = 0
Bu tür denklemleri çözmek için birkaç farklı yöntem kullanılabilir. En sık kullanılan yöntemler:
- Faktöriyel Ayırma Yöntemi:
Denklemi çarpanlarına ayırarak çözüm bulunur. Eğer denklemin çarpanlara ayrılabilen bir yapısı varsa, bu yöntem kullanılır. - Delta (Diskriminant) Yöntemi:
Diskriminant (Δ) formülü kullanılarak kökler bulunur. Diskriminant formülü:
Δ = b² – 4ac
- Eğer Δ > 0 ise denklemin iki farklı reel kökü vardır.
- Eğer Δ = 0 ise denklemin iki eşit reel kökü vardır.
- Eğer Δ < 0 ise denklemin reel kökü yoktur, karmaşık kökler vardır.
Kökler formülü:
x₁, x₂ = (-b ± √Δ) / 2a
Çözümlü Örnek Sorular
Soru 1:
x² – 5x + 6 = 0 denkleminin köklerini bulunuz.
A) 2 ve 3
B) -2 ve -3
C) 1 ve 6
D) -1 ve -6
E) 0 ve 5
Çözüm:
Verilen denklemi çarpanlarına ayıralım:
x² – 5x + 6 = (x – 2)(x – 3) = 0
Buradan x = 2 ve x = 3 kökleri bulunur.
Cevap: A
Soru 2:
x² + 4x + 4 = 0 denkleminin köklerini bulunuz.
A) 2 ve 2
B) -2 ve -2
C) 1 ve 4
D) -1 ve 4
E) 0 ve -4
Çözüm:
Denklemi çarpanlarına ayıralım:
x² + 4x + 4 = (x + 2)(x + 2) = 0
Buradan x = -2 ve x = -2 yani çift kök bulunur.
Cevap: B
Soru 3:
2x² – 3x + 1 = 0 denkleminin köklerini bulunuz. (Delta yöntemi kullanarak)
A) 1 ve 2
B) 1 ve 3
C) 1/2 ve 1
D) -1 ve 1
E) -1/2 ve -1
Çözüm:
Denklemin katsayıları:
a = 2, b = -3, c = 1
Diskriminantı hesaplayalım:
Δ = b² – 4ac
Δ = (-3)² – 4(2)(1)
Δ = 9 – 8 = 1
Kökler formülü:
x₁, x₂ = (-b ± √Δ) / 2a
x₁, x₂ = (3 ± 1) / 4
x₁ = (3 + 1) / 4 = 4 / 4 = 1
x₂ = (3 – 1) / 4 = 2 / 4 = 1/2
Cevap: C
Soru 4:
x² – 6x + 9 = 0 denkleminin köklerini bulunuz.
A) 3 ve 3
B) -3 ve -3
C) 0 ve 3
D) -3 ve 0
E) 1 ve 3
Çözüm:
Denklemi çarpanlarına ayıralım:
x² – 6x + 9 = (x – 3)(x – 3) = 0
Buradan x = 3 ve x = 3 yani çift kök bulunur.
Cevap: A
Soru 5:
x² – 2x – 8 = 0 denkleminin köklerini bulunuz.
A) 4 ve -2
B) 2 ve -4
C) -2 ve 3
D) 3 ve -2
E) 0 ve 4
Çözüm:
Verilen denklemi çarpanlarına ayıralım:
x² – 2x – 8 = (x – 4)(x + 2) = 0
Buradan x = 4 ve x = -2 kökleri bulunur.
Cevap: A
2. Dereceden Denklemler 1 Rehber Matematik
2. Dereceden Denklemler 2 Rehber Matematik
2. Dereceden Denklemler 3 Rehber Matematik
2. Dereceden Denklemler 4 Rehber Matematik
2. Dereceden Denklemler 5 Rehber Matematik
2. Dereceden Denklemler 6 Rehber Matematik
2. Dereceden Denklemler Soru Çözümü Rehber Matematik
















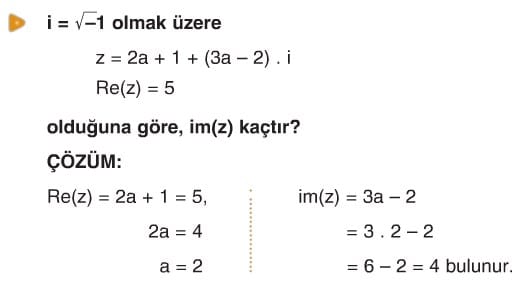


























































Gerçekten tüm derslerde çok başarı bi anlatınız var emeğiniz için teşekkür ederiz
Covitin bizi zorlaması üstüne üstlük okullara ara verilmesi bizi bitirdi ama olsun en azından elimizde notlar varrr.
corona yaktın beni
canlı derslere giremediğimden bu konuyu anlamamıştım. ama şimdi çok iyi biliyom çok tşkkr
Çok güzel, beğendim. Güzel site.