10. sınıf İki nokta arasındaki uzaklık konu anlatımı ders notu matematik soru çözümleri

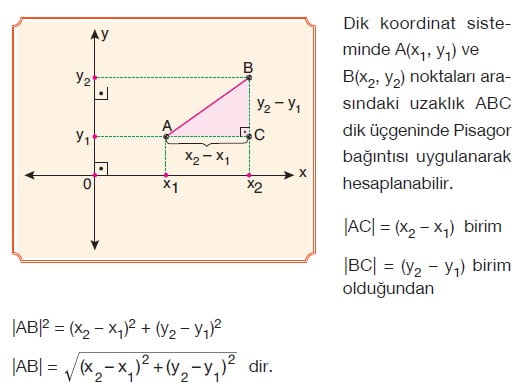
Dik koordinat sisteminde A(x1, y1) ve B(x2, y2) noktaları arasındaki uzaklık ABC dik üçgeninde pisagor bağıntısı uygulanarak bulunur.

İki Nokta arasındaki uzaklık çözümlü örnekler

Analitik düzlemde A(x₁, y₁) ve B(x₂, y₂) noktaları arasındaki uzaklık, Pisagor teoremi kullanılarak hesaplanır. Uzaklık formülü şu şekildedir:

|AB| = √((x₂ – x₁)² + (y₂ – y₁)²)

Bu formül, iki nokta arasındaki yatay ve dikey farkların karelerinin toplamının karekökünü alarak bulunur.

Soru 1:
A noktası (5, 4) ve B noktası (-4, -2) olduğuna göre, A ve B noktaları arasındaki uzaklığı hesaplayınız.

Çözüm:
|AB| = √((-4 – 5)² + (-2 – 4)²)
|AB| = √((-9)² + (-6)²)
|AB| = √(81 + 36)
|AB| = √117
|AB| = 3√13
Cevap: 3√13

Soru 2:
A noktası (7, 6) ve B noktası (3, 3) olduğuna göre, A ve B arasındaki uzaklığı bulunuz.

Çözüm:
|AB| = √((3 – 7)² + (3 – 6)²)
|AB| = √((-4)² + (-3)²)
|AB| = √(16 + 9)
|AB| = √25
|AB| = 5
Cevap: 5

Soru 3:
C noktası (1, 2) ve D noktası (4, -2) olduğuna göre, C ve D arasındaki uzaklık kaç birimdir?

Çözüm:
|CD| = √((4 – 1)² + (-2 – 2)²)
|CD| = √(3² + (-4)²)
|CD| = √(9 + 16)
|CD| = √25
|CD| = 5
Cevap: 5

Soru 4:
E noktası (2, -3) ve F noktası (2, 5) ise, E ve F noktaları arasındaki uzaklık kaç birimdir?

Çözüm:
|EF| = √((2 – 2)² + (5 + 3)²)
|EF| = √(0 + 8²)
|EF| = √64
|EF| = 8
Cevap: 8

Soru 5:
G noktası (0, 0) ve H noktası (6, 8) olduğuna göre, G ve H noktaları arasındaki uzaklığı bulunuz.

Çözüm:
|GH| = √((6 – 0)² + (8 – 0)²)
|GH| = √(6² + 8²)
|GH| = √(36 + 64)
|GH| = √100
|GH| = 10
Cevap: 10

Soru 6:
K noktası (3, -5) ve L noktası (-2, -1) olduğuna göre, K ve L noktaları arasındaki uzaklığı bulunuz.

Çözüm:
|KL| = √((-2 – 3)² + (-1 + 5)²)
|KL| = √((-5)² + (4)²)
|KL| = √(25 + 16)
|KL| = √41
Cevap: √41

Soru 7:
M noktası (-7, 3) ve N noktası (1, -2) olduğuna göre, M ve N noktaları arasındaki uzaklık kaç birimdir?

Çözüm:
|MN| = √((1 + 7)² + (-2 – 3)²)
|MN| = √((8)² + (-5)²)
|MN| = √(64 + 25)
|MN| = √89
Cevap: √89

Soru 8:
P noktası (0, 0) ve Q noktası (9, 12) olduğuna göre, P ve Q arasındaki uzaklığı bulunuz.

Çözüm:
|PQ| = √((9 – 0)² + (12 – 0)²)
|PQ| = √(9² + 12²)
|PQ| = √(81 + 144)
|PQ| = √225
|PQ| = 15
Cevap: 15

Soru 9:
R noktası (4, -3) ve S noktası (-1, 1) olduğuna göre, R ve S noktaları arasındaki uzaklık kaç birimdir?

Çözüm:
|RS| = √((-1 – 4)² + (1 + 3)²)
|RS| = √((-5)² + (4)²)
|RS| = √(25 + 16)
|RS| = √41
Cevap: √41

Soru 10:
T noktası (6, -8) ve U noktası (-6, 8) olduğuna göre, T ve U noktaları arasındaki uzaklığı hesaplayınız.

Çözüm:
|TU| = √((-6 – 6)² + (8 + 8)²)
|TU| = √((-12)² + (16)²)
|TU| = √(144 + 256)
|TU| = √400
|TU| = 20
Cevap: 20