Bileşke Fonksiyon 10. Sınıf
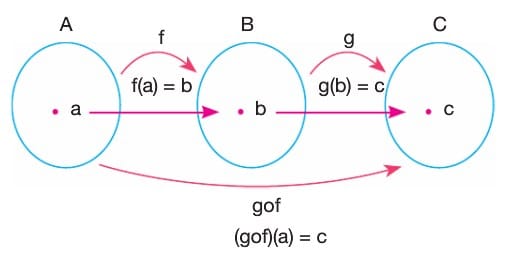
Yukarıdaki şemada verildiği gibi
f: A → B ve g: B → C
fonksiyonları için A kümesindeki her elemanı, C kümesindeki yalnız bir elemana eşleyen fonksiyona bileşke fonksiyon denir. Bu fonksiyon gof şeklinde gösterilir ve
Bileşke Fonksiyon Soruları ve Çözümleri
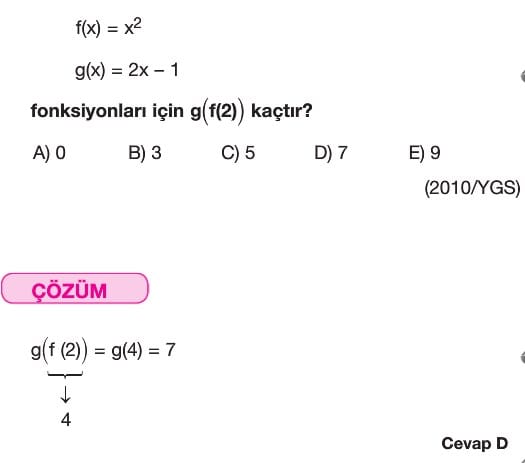
Çözümlü Örnek Test Soruları: Bileşke Fonksiyon
Soru 1:
f(x) = 2x + 3 ve g(x) = x – 1 fonksiyonları veriliyor. (f ∘ g)(x) nedir?
a) 2x + 1
b) 2x + 5
c) 2x – 1
d) x + 2
Çözüm: (f ∘ g)(x) = f(g(x)) = f(x – 1) = 2(x – 1) + 3 = 2x – 2 + 3 = 2x + 1. Cevap: a)
Soru 2:
f(x) = x² ve g(x) = 3x + 4 fonksiyonları için (g ∘ f)(x) nedir?
a) 3x² + 4
b) x² + 4
c) 3x + 4
d) 3x² – 4
Çözüm: (g ∘ f)(x) = g(f(x)) = g(x²) = 3(x²) + 4 = 3x² + 4. Cevap: a)
Soru 3:
f(x) = x + 2 ve g(x) = x² fonksiyonları veriliyor. (f ∘ g)(x) nedir?
a) x² + 2
b) x + 4
c) 2x + 4
d) x² – 2
Çözüm: (f ∘ g)(x) = f(g(x)) = f(x²) = x² + 2. Cevap: a)
Soru 4:
f(x) = 3x – 1 ve g(x) = x + 2 fonksiyonları veriliyor. (g ∘ f)(x) nedir?
a) 3x + 1
b) 3x – 3
c) x + 2
d) x – 1
Çözüm: (g ∘ f)(x) = g(f(x)) = g(3x – 1) = (3x – 1) + 2 = 3x + 1. Cevap: a)
Soru 5:
f(x) = 2x + 1 ve g(x) = x/2 fonksiyonları veriliyor. (f ∘ g)(x) nedir?
a) x + 1
b) x/2 + 1
c) x + 1/2
d) x
Çözüm: (f ∘ g)(x) = f(g(x)) = f(x/2) = 2(x/2) + 1 = x + 1. Cevap: a)
Soru 6:
f(x) = x – 3 ve g(x) = x² + 1 fonksiyonları için (g ∘ f)(x) nedir?
a) x² – 6x + 10
b) x² – 3
c) x² + x – 2
d) x – 2
Çözüm: (g ∘ f)(x) = g(f(x)) = g(x – 3) = (x – 3)² + 1 = x² – 6x + 9 + 1 = x² – 6x + 10. Cevap: a)
Soru 7:
f(x) = 5x ve g(x) = x – 2 fonksiyonları veriliyor. (f ∘ g)(x) nedir?
a) 5x – 2
b) 5x – 10
c) x – 2
d) 3x
Çözüm: (f ∘ g)(x) = f(g(x)) = f(x – 2) = 5(x – 2) = 5x – 10. Cevap: b)
Soru 8:
f(x) = x² – 1 ve g(x) = x + 1 fonksiyonları için (f ∘ g)(x) nedir?
a) x² + 2x
b) x² – 1
c) x² + 2x + 1
d) x² + x
Çözüm: (f ∘ g)(x) = f(g(x)) = f(x + 1) = (x + 1)² – 1 = x² + 2x + 1 – 1 = x² + 2x. Cevap: a)
Fonksiyonlarda bileşke işleminin değişme özelliği yoktur. Yani, (fog)(x) ≠ (gof)(x)
Fonksiyonlarda bileşke işleminin birleşme özelliği vardır. Yani fogoh = fo(goh) = (fog)oh = f(g(h))
İki fonksiyondan yeni bir fonksiyon elde etmenin dört işlem dışında bir yolu daha vardır. Yeni fonksiyon, verilen iki fonksiyon birleştirilerek elde edildiğinden bu fonksiyon oluşturma işlemine bileşke alma denir. Şimdi bileşke fonksiyonun tanımını verebiliriz.
Bileşke fonksiyon: f ve g iki fonksiyon olsun. (fog)(x) = f(g(x)) şeklinde gösterilmesine f ve g nin bileşkesi denir. A, B ve C boş kümeden farklı birer küme olmak üzere,
f: A ≠ B ve g: B ≠ C şeklinde tanımlanan iki fonksiyon olsun. A kümesindeki elemanları f ve g fonksiyonlarını kullanarak C kümesindeki elemanlar ile eşleyen yeni fonksiyona bileşke fonksiyon denir.
gof: A ≠ C olmak üzere, (gof)(x) = g(f(x)) kuralı ile tanımlı fonksiyon: g ile f nin hileşkesi denir. Aşağıdaki şemayı inceleyelim.
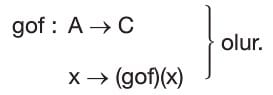



















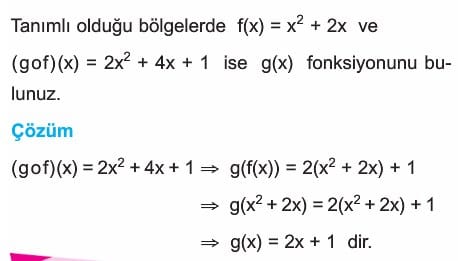


f(3)=2g(0)=1 g(1)=2 olduğuna göre f(1)+g(2) kaçtır
Verdiğiniz bilgiler eksik bu haliyle bir şey yapılamaz
(fogoh)=
(x)
Nedir cevap
merhaba, gof(x)=sin|x| fog(x)=(sin√x)^2
f(x), g(x) nedir bulabilirr misiniz?
çok iyi olmuş
Örnek: A = –2, –1, 0, 1, 2^ , B = 0, 1, 4 ^ , C = –2, –1, 1, 2, 3^ kümeleri veriliyor.
f : A Z B , f(x) = x 2 ve g : B Z C , g(x) = x – 2 olduôuna gÌre f ve g fonksiyonlarnn
tanm ve gÌrüntü kümelerini öema ile gÌsterelim.
%aha sonra g o f fonksiyonunun tanm ve gÌrüntü kümelerini öema ile
gÌsterip kuraln bulalm.
f ( x ) = x 2 fonksiyonunun görüntü kümesi, f ( A ) = { 0, 1, 4 } tür. [ f ( A ) = B dir. ]
g(x) = x – 2 fonksiyonunun görüntü kümesi, g ( B ) = g [ f ( A )] = { –2, –1, 2 } dir.
Buna göre f ve g fonksiyonlarnn tanm ve görüntü kümeleri i 62. ôekil u deki
gibidir.
i 62. ôekiludeki õemada görüldüğü gibi A kümesinin elemanlar, f ve g fonksiyonlarnn
yardm ile C kümesindeki elemanlara eõlenmiõtir.
Burada f ve g fonksiyonlarndan yararlanlarak A dan C ye yeni bir fonksiyon
elde edilmiõtir. Bu fonksiyon f ile g fonksiyonlarnn bileõke fonksiyonu olan
g o f fonksiyonudur.
g o f fonksiyonunun görüntü kümesi bulunurken tanm kümesindeki bir elemann
önce f fonksiyonu altndaki görüntüsü, sonra da bu görüntünün g
fonksiyonu altndaki görüntüsü bulunur.
Yani ( g o f ) : A Z C, ( g o f ) ( x ) = g [ f ( x ) ] dir.
Buna göre yukardaki gof fonksiyonunun kuraln bulalm.
Bir süt fabrikasnda kullanlan iki makineden birincisi süt õiõelerine sütü doldurmak için ikincisi ise õiõelerin kapaklarn monte etmek için kullanlrken fabrikaya daha teknoloKik olan üçüncü bir makine alnyor. Bu makine hem süt õiõelerine sütü dolduruyor hem de õiõelerin kapaklarn monte ediyor. Buna göre srasyla birinci ve ikinci makineye giren bir süt õiõesi ile sadece üçüncü makineye giren baõka bir süt õisesi hangi aõamalardan geçer Süt õiõesine yaplan iõlemler iki durumda da ayn olur mu Sizce bu iki õiõe makinelerden çktktan sonra içerik bakmndan ayn özelliklere sahip midir?
Boõ olmayan A, B ve C kümeleri için f : A Z B, g : B Z C fonksiyonlar verilsin. f ve g fonksiyonlar yardmyla A dan C ye tanmlanan yeni fonksiyona f ile g fonksiyonlarnn bileökesi denir ve gof biçiminde gösterilir.