Örneğin;
° Saatte ortalama 80 km yol alan bir aracın 5 saatte alacağı yol,
80.5 = 400 km dir.
Hız.Zaman = Yol

° Saatte 30 km yol alan bir bisikletlinin 60 km Iik mesafeyi alabileceği süre,
60 : 30 = 2 saattir.
Yol : Hız = Zaman

° 540 km lik bir mesafeyi 6 saatte alan bir otobüsün hızı,
540 : 6 = 90 km/sa tir.
Yol : Zaman = Hız

Hareket (Hız) Problemleri Çözümlü Sorular

Şenol Hoca Hareket Problemleri Konu Anlatımı Video

Hocalara Geldik Hareket Problemleri Konu Anlatımı Video

Çözümlü Örnek Test Soruları

1. Bir araç saatte 60 km hızla 3 saat yol alıyor. Bu araç toplamda kaç kilometre yol gitmiştir?
A) 120 km
B) 150 km
C) 180 km
D) 200 km
Cevap: C) 180 km
Çözüm: Yol = Hız × Zaman formülüne göre, 60 km/sa × 3 saat = 180 km yol alınmıştır.

2. İki araç aynı anda bir noktadan zıt yönlere hareket ediyor. Birinci aracın hızı 70 km/sa, ikinci aracın hızı ise 50 km/sa’dır. 2 saat sonra araçlar arasındaki mesafe kaç kilometre olur?
A) 180 km
B) 240 km
C) 260 km
D) 300 km
Cevap: B) 240 km
Çözüm: Araçlar zıt yönlere hareket ettiğinden toplam hızları 70 + 50 = 120 km/sa olur. 2 saat sonra 120 × 2 = 240 km mesafe oluşur.

3. Bir öğrenci, sabah evinden okula 5 km/sa hızla gidiyor ve 2 saat sonra okula varıyor. Aynı yolu akşam 4 km/sa hızla geri dönüyor. Gidiş ve dönüş toplamda kaç saatte tamamlanmıştır?
A) 4 saat
B) 5 saat
C) 6 saat
D) 7 saat
Cevap: B) 5 saat
Çözüm: Gidiş süresi 2 saattir. Dönüş süresi ise 10 km ÷ 4 km/sa = 2.5 saattir. Toplam süre 2 + 2.5 = 5 saattir.

4. 150 km uzaklıktaki iki şehirden, biri 80 km/sa hızla diğeri 70 km/sa hızla birbirine doğru hareket eden iki araç aynı anda hareket ediyor. Kaç saat sonra buluşurlar?
A) 0.5 saat
B) 1 saat
C) 1.5 saat
D) 2 saat
Cevap: C) 1.5 saat
Çözüm: Toplam hızları 80 + 70 = 150 km/sa olur. 150 km ÷ 150 km/sa = 1.5 saat sonra buluşurlar.

5. Bir bisikletli, birinci yarım saatte 15 km/sa hızla, ikinci yarım saatte ise 10 km/sa hızla hareket ediyor. Bisikletlinin toplamda aldığı yol kaç kilometredir?
A) 10 km
B) 12.5 km
C) 15 km
D) 20 km
Cevap: B) 12.5 km
Çözüm: İlk yarım saatte alınan yol 15 × 0.5 = 7.5 km’dir. İkinci yarım saatte alınan yol 10 × 0.5 = 5 km’dir. Toplam yol 7.5 + 5 = 12.5 km’dir.

6. Bir koşucu, bir parkurda 4 km/sa hızla koşuyor. Koşucu, parkurun tamamını 45 dakikada bitiriyorsa parkurun uzunluğu kaç kilometredir?
A) 2 km
B) 3 km
C) 4 km
D) 5 km
Cevap: B) 3 km
Çözüm: 45 dakika = 0.75 saattir. Yol = Hız × Zaman formülüne göre, 4 × 0.75 = 3 km’dir.

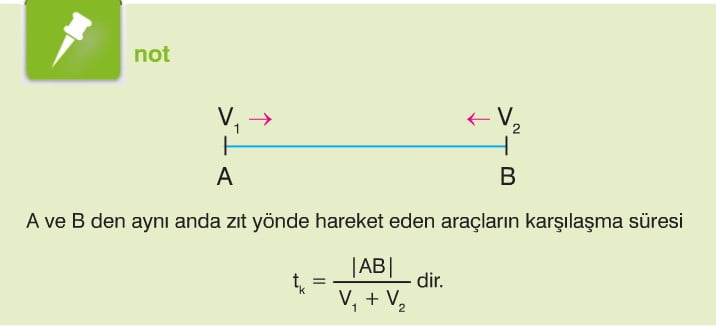
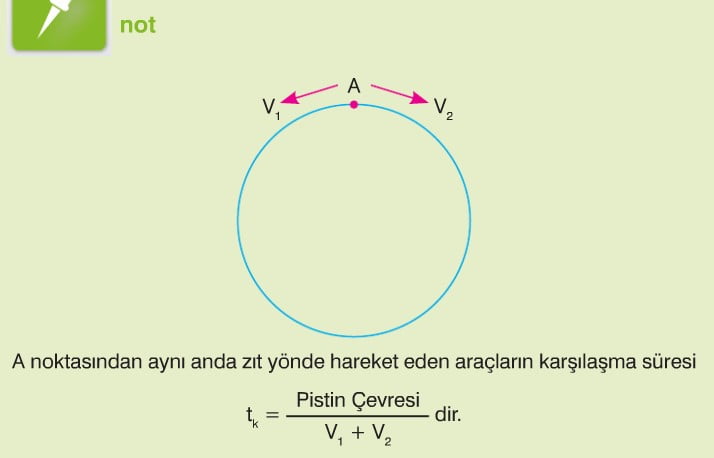
Saatteki hızları v1 km ve v2 km olan iki araç aralarında x km bulunan A ve B noktalarından aynı anda birbirlerine doğru hareket ettiklerinde karşılaşma süresi t saat olsun. Bu iki araç arasındaki yolun uzunluğu araçların aldıkları yolların toplamına eşittir. Buna göre,
|AB| = v1.t + v2.t dir.
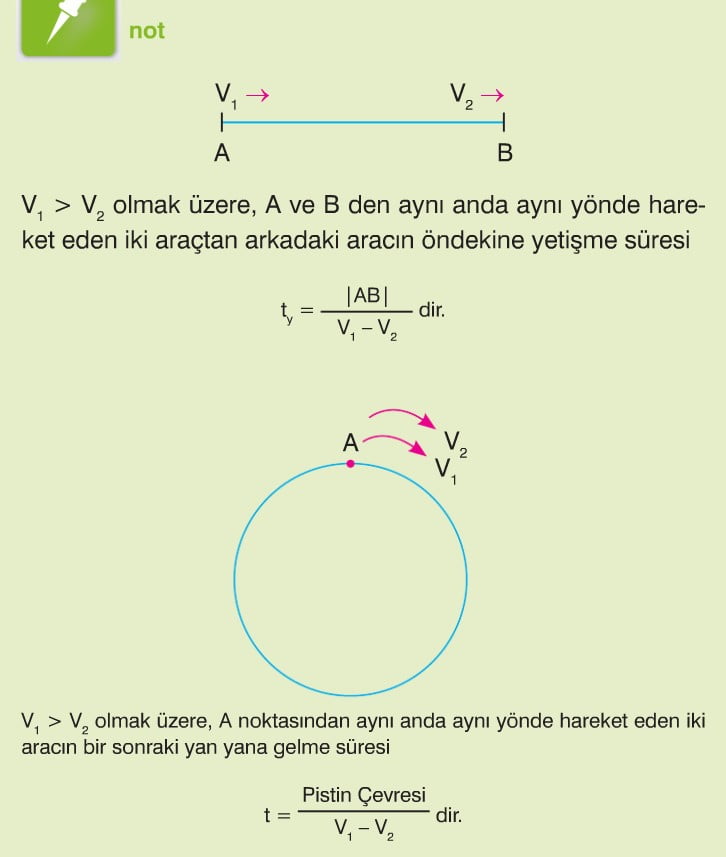
v1 > v2 olmak üzere, A noktası ile B noktasından hızları sırasıyla v1 km/saat ve v2 km/saat olan iki araç aynı anda aynı yöne doğru hareket ettiğinde hızlı olan diğerine t saat sonra yetişsin. Bu durumda
|AB| = v1.t – v2.t dir.
Nehir problemlerinde hareketlinin hızı, akıntının yönüne göre belirlenir. Bir kayığın akıntı ile aynı yönde gidip akıntıya ters yönde döndüğünü varsayalım.
Akıntı hızı: va
Kayığın suya göre hızı: vk
vk > va olmak üzere,
Kayığın yere göre gidiş hızı: vk + va
Kayığın yere göre dönüş hızı: vk – va olur.
Bir hareketli aldığı toplam yolun uzunluğunun, bu yolu aldığı toplam süreye bölümüne ortalama hız denir. Buna göre, ortalama hız problemlerinde,
Ortalama Hız = Toplam Yol / Toplam Zaman formülü kullanılır.
Örnek;
° Saatte ortalama 80 km yol alan bir aracın 5 saatte alacağı yol,
80.5 = 400 km dir.
Hız.Zaman = Yol
° Saatte 30 km yol alan bir bisikletlinin 60 km Iik mesafeyi alabileceği süre,
60 : 30 = 2 saattir.
Yol : Hız = Zaman
° 540 km lik bir mesafeyi 6 saatte alan bir otobüsün hızı,
540 : 6 = 90 km/sa tir.
Yol : Zaman = Hız
Hareket Problemleri diğer bir ifadeyle hız problemleri 9. sınıf matematik müfredatında yer almaktadır. Hareket problemlerinden kpss ve ygs matematik sınavlarında soru çıkmaktadır.
Yol = Hız . Zaman
Yol = x , Hız = V , Zaman = t ise hareket formülümüz x = V. t şeklindedir.
Ortalama Hız = Toplam Yol / Toplam Zaman
Örnek: Birinin saatteki hızı diğerinin saatteki hızından 40 km fazla olan iki araç aynı anda A noktasından B noktasına doğru hareket ediyorlar. Hızlı olan araç 3 saatte, yavaş olan araç 5 saatte B noktasına vardığına göre, A ile B noktası arasındaki uzaklığı bulalım.
Örnek: A şehrinden B şehrine saatte 80 km hızla giden bir araç, hiç beklemeden B den A ya saatte 120 km hızla dönüyor. Bu aracın gidiş dönüşü toplam 10 saat sürdüğüne göre, A dan B ye kaç saatte gittiğini bulalım.
Örnek: İki hareketli çevresi 720 metre olan kare şeklindeki ABCD pistinin A noktasından aynı anda 3V ve 5V hızlarıyla şekildeki yönlerde harekete başlıyorlar. Bu hareketliler ilk kez E noktasında karşılaştığına göre, |DE| yolunun kaç metre olduğunu bulalım.
Örnek: Kubilay, yurttan okula 20 dakikada varabiliyor. Yurttan yola çıkan Kubilay 5 dakika sonra kitabını yurtta unuttuğunu fark ediyor ve yurda dönerek kitabını alıp tekrar okula gidiyor. Okula zamanında varması için kitabı unuttuğu andan itibaren hızını kaç katına çıkarması gerektiğini bulalım.
Örnek: A ve B kentlerinden şekildeki hızlarla, aynı anda birbirlerine doğru hareket eden iki araç 15 dakika sonra D noktasında karşılaşıyorlar. İki araç, aynı anda ve aynı yönde hareket etselerdi A dan hareket eden araç, diğerine C noktasında yetişecektir. Buna göre, |BC| yolunun uzunluğunu bulalım.
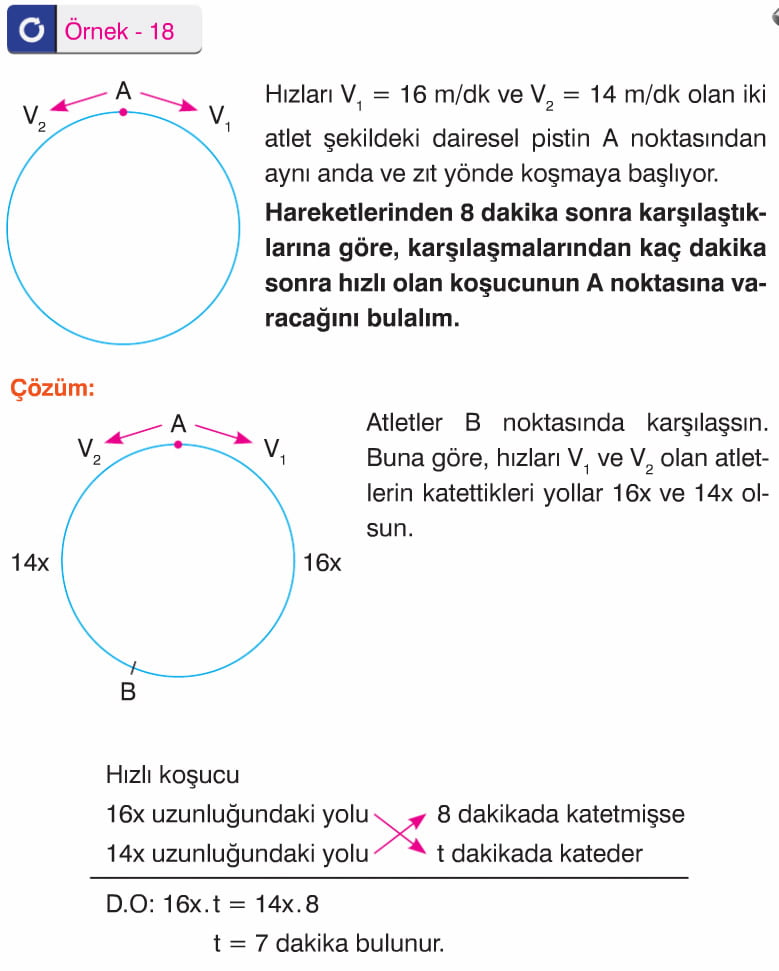
Örnek: Hızları V1 = 16 m/dk ve V2 = 14 m/dk olan iki atlet şekildeki dairesel pistin A noktasından aynı anda ve zıt yönde koşmaya başlıyor. Hareketlerinden 8 dakika sonra karşılaştıklarına göre, karşılaşmalarından kaç dakika sonra hızlı olan koşucunun A noktasına varacağını bulalım.
Örnek: A ve B şehrinden şekildeki hızlarla aynı anda ve birbirlerine doğru hareket eden iki araç 3 saat sonra karşılaştıklarına göre, bu araçlar aynı anda aynı yönde (C şehrine doğru) hareket etselerdi hızlı olan aracın diğer araca kaç saat sonra yetişebileceğini bulalım.
Örnek: Hızı saatte 76 km olan bir hareketli A kentinden, hızı saatte 54 km olan bir hareketli B kentinden aynı anda birbirine doğru hareket ediyorlar. A kenti ile B kenti arasındaki uzaklık 585 km olduğuna göre, hareketliler kaç saat sonra karşılaşırlar?
Örnek: Bir araç A kentinden B kentine 90 km/sa hızla giderse planlanan süreden 1 saat erken varıyor, eğer 60 km/sa hızla giderse planlanan süreden 2 saat geç kalıyor. Buna göre, A ve B kentleri arası uzaklık kaç km dir?
Örnek: A ve B kentleri arası 450 km dir.İki hareketli A ve B den aynı anda karşılıklı olarak birbirlerine doğru hareket ediyorlar. 4 saat sonra karşılaşmalarına 34 km mesafe kaldığına göre, bu iki hareketlinin hızları toplamı saatte kaç km dir?
Örnek: A ile B arası 270 km dir. Hızları saatte 6v km ve saatte 10V km olan iki araç A noktasından aynı anda aynı yöne hareket ediyorlar. Araçlardan biri B noktasına diğeri C noktasına varıp hiç durmadan geri dönüyorlar ve A noktasına aynı anda varıyorlar. Buna göre, B ile C arası kaç km dir?
Örnek: Çevre uzunluğu 480 m olan yukarıdaki çembersel pistin A noktasından, 118 m/dk ve 130 m/dk hızıyla iki bisikletli aynı anda aynı yöne doğru yola çıkıyor. Buna göre, hızlı olan bisikletli diğerine ilk kez kaç dakika sonra yetişir?
Örnek: A noktasından B noktasına giden ve durmadan geri dönen bir koşucu, gidişinde ortalama dakikada 600 m, dönüşünde dakikada 500 m alıyor. Bu koşucu A dan B ye 33 dakikada gidip geldiğine göre, A ile B arası kaç km dir?
Örnek: Dairesel pistin A noktasından, 15 m/sn ve 24 m/sn hızıyla iki hareketli aynı anda birbirine doğru harekete başlıyor. Bu iki hareketli 12 saniye sonra karşılaşıyor. Hareketliler karşılaştıktan sonra yola devam ettiklerine göre, hızı 24 m/sn olan hareketli karşılaştıktan kaç saniye sonra A noktasına gelir?
Örnek: Bir banka, dolar olarak yatırılan paraya yıllık % 8 faiz vermektedir. Yunus bu bankaya dolar olarak yatırdığı parasını 1 yılın sonunda faiziyle birlikte çekmiş ve Türk lirasına çevirdiğinde toplam 324 TL kâr elde etmiştir. Yunus, parasını bankaya yatırdığında doların kuru 2,7 TL, bankadan çektiğinde 3 TL olduğuna göre, başlangıçta kaç dolar yatırmıştır?