Gerçek sayıların işlem özellikleri, matematiğin temel yapı taşlarından biridir ve bu özelliklerin anlaşılması, öğrencilerin matematiksel düşünme ve problem çözme becerilerini geliştirmelerine büyük katkı sağlar. Bu konu, toplama, çıkarma, çarpma ve bölme gibi temel işlemlerin gerçek sayılar üzerinde nasıl uygulandığını ve bu işlemlerin sahip olduğu özel kuralları inceler. Bu kurallar, matematiksel ifadelerin düzenlenmesi, sadeleştirilmesi ve çözümlenmesi için kritik öneme sahiptir.

9. Sınıf Gerçek Sayıların İşlem Özellikleri Testleri

9. Sınıf Gerçek Sayıların İşlem Özellikleri Ders Notu

Önerme Kavramı

• Doğru ya da yanlış kesin bir hüküm (yargı) bildiren ifadelere önerme adı verilir.
• Matematikte önermeler genellikle p, q, r, s gibi küçük harflerle gösterilir.
• Matematiksel önermeler sözel veya sembolik dille ifade edilebilir.
• Soru, emir, istek, ünlem, belirten ifadeler ile öznel ifadeler önerme belirtmezler.

Örnek: “Türkiye’nin başkenti Ankara’dır.” ifadesi bir önermedir. Ancak, “En güzel dondurma kakaolu dondurmadır” ifadesi bir önerme değildir.

• Bir önermedeki hükmün doğruluğuna ya da yanlışlığına önermenin doğruluk değeri denir.
• Bir önerme doğru bir hüküm bildiriyorsa doğruluk değeri “1” ile, yanlış bir hüküm bildiriyorsa doğruluk değeri “0” ile gösterilir.

Örnek:

• p: “4 + 3 = 7” önermesi doğrudur. Doğruluk değeri 1’dir. p ≡ 1 ile gösterilir.
• q: “5 > 7” önermesi yanlıştır. Doğruluk değeri 0’dır. q ≡ 0 ile gösterilir.

Matematikte kavramlar, kavramlara ait özellikler, işlemlerden elde edilen sonuçlar sözel veya sembolik olarak ifade edilebilir. Bu ifadelerden bazıları doğrulanabilir veya yanlışlanabilir.

Matematikte Sembolik Dil

• İki veya daha fazla önermeyi birlikte ifade edebilmek için başlangıç veya gerektirmelerden faydalanılır.
• Gerçek sayılarda işlem özelliklerini ifade eden önermeler, sembolik dil kullanılarak ifade edilebilir.
• Sembolik dil, matematiksel ifadelerin standartlaştırılmasına ve genelleştirilmesine imkân sağlar.
• Bunun için bağlaçlar (ve, veya, ya da), niceleyiciler (her, bazı) ve gerektirmeler (ise, ancak ve ancak) kullanılır.

Aşağıdaki tabloda matematiksel semboller ve anlamları gösterilmiştir.

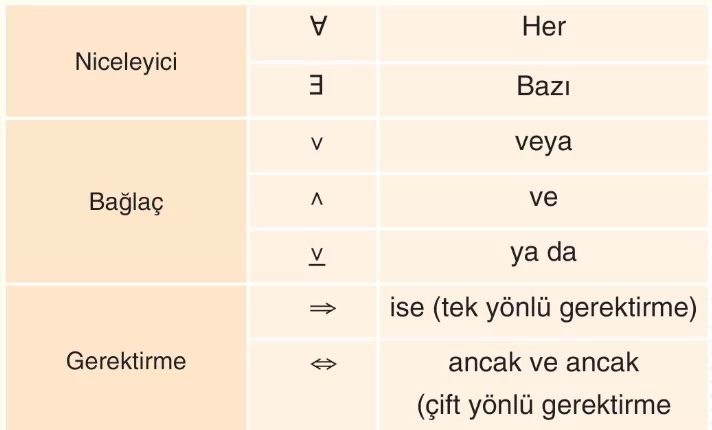
Niceleyiciler

Önüne geldiği elemanın çokluğunu (niceliğini) ifade eden sembollere niceleyici denir.

∀, bütün, tüm (Evrensel niceleyici)
∃, en az bir (Varlıksal niceleyici)

• ∀ niceleyici bulunan bir önermeyi sağlayamayan en az bir tane örnek bulunursa önerme yanlış, bulunamazsa önerme doğrudur.
• ∃ niceleyicisi bulunan bir önermeyi sağlayan en az bir tane örnek bulunursa önerme doğru, bulunmazsa önerme yanlıştır.

Örnek:

• p: “∀x ∈ ℝ için x² > 0”
  Önerme 0 ∈ ℝ için sağlamaz, dolayısıyla p’nin doğruluk değeri sıfırdır.
• q: “∃x ∈ ℕ için 2x – 3 ≤ 5”
  Önerme x ≤ 4 için yani 0, 1, 2, 3, 4 doğal sayıları için sağlar. Dolayısıyla q önermesinin doğruluk değeri birdir.

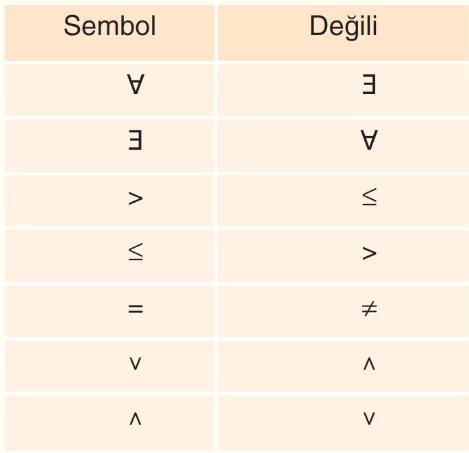
Bir önermenin hükmünün olumsuzu alınarak yapılan yeni önermeye bu önermenin değili (olumsuzu) denir.

Örnek:
p: “√3 bir rasyonel sayıdır.” önermesinin değili,
p’: “√3 bir rasyonel sayı değildir.” olur.

Gerçek Sayılarda İşlem Özellikleri

Değişme Özelliği:
∀ m, n ∈ ℝ için m + n = n + m ve m • n = n • m olur.

Birleşme Özelliği:
∀ m, t, n ∈ ℝ için m + (t + n) = (m + t) + n ve m • (t • n) = (m • t) • n olur.

Birim (Etkisiz) Eleman:
∀ m ∈ ℝ için m + 0 = 0 + m olduğundan toplama işleminin birim (etkisiz) elemanı 0’dır.
m • 1 = 1 • m olduğundan çarpma işleminin birim (etkisiz) elemanı 1’dir.

Ters Eleman:
∀ m ∈ ℝ ve m ≠ 0 için m + (−m) = (−m) + m = 0 olduğundan m’nin toplama işlemine göre tersi −m’dir.
m • 1/m = 1/m • m olduğundan m’nin çarpma işlemine göre tersi 1/m = m⁻¹’dir.

Yutan Eleman:
∀ m ∈ ℝ için m • 0 = 0 • m = 0 olduğundan çarpma işleminin yutan elemanı 0’dır.
Gerçek sayılarda toplama, çıkarma ve bölme işleminin yutan elemanı yoktur.

Çarpma İşleminin Toplama ve Çıkarma İşlemi Üzerine Dağılma Özelliği:
∀ m, t, n ∈ ℝ için
m • (t + n) = m • t + m • n
m • (t − n) = m • t − m • n olur.

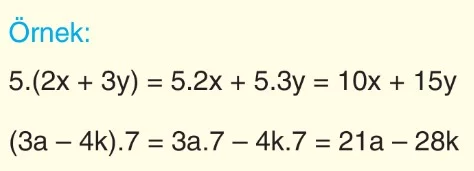
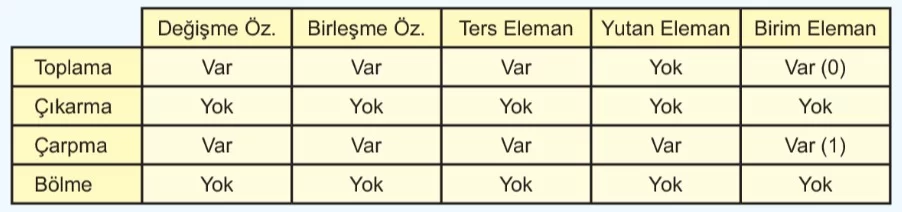
Aşağıdaki şemada işlemlere göre özelliklerin varlıkları belirtilmiştir.

Özdeşlikler ve Geometrik Yorumları

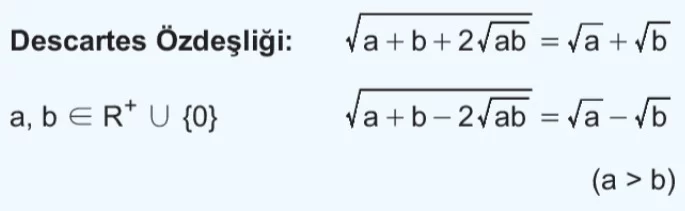
Değişkenlere verilen her değer için doğru olan cebirsel ifadelere “özdeşlik” denir. Aşağıda sık kullanılan bazı özdeşlikler verilmiştir.

Her a, b ∈ R için:

• Tam Kare İfadeler
  İki Terimin Toplamının Karesi:
  (a + b)² = a² + 2ab + b²
  İki Terimin Farkının Karesi:
  (a – b)² = a² – 2ab + b²
• İki Kare Farkı:
  a² – b² = (a – b) • (a + b)

Gerçek Sayıların İşlem Özellikleri Çözümlü Sorular

---

Çözümlü Örnek Test Soruları

1. Soru: Bir matematik öğretmeni, sınıfında gerçek sayıların işlem özelliklerini örneklerle anlatmaktadır. Öğretmen, toplama işleminde “değişme” ve “birleşme” özelliklerinin gerçek sayılar kümesinde geçerli olduğunu vurgulamıştır. Öğrencilerden biri, öğretmenin söylediği özelliklerin doğru olup olmadığını sorgulamak için aşağıdaki önerileri sunar:

• I. a + b = b + a, bu bir değişme özelliğidir.
• II. (a + b) + c = a + (b + c), bu bir birleşme özelliğidir.
• III. a + 0 = a, bu bir ters eleman özelliğidir.

Bu önerilerden hangileri doğrudur?

A) Yalnız I
B) I ve II
C) I ve III
D) II ve III
E) I, II ve III

Çözüm:
Değişme özelliği I ifadesinde doğru bir şekilde verilmiştir. II ifadesi birleşme özelliğidir ve doğrudur. III ifade ise birim (etkisiz) eleman özelliğini tanımlamaktadır, ters eleman özelliği değildir. Bu durumda doğru cevap B

2. Soru: Aşağıdaki ifadelerden hangisi “sembolik dil” kullanılarak doğru şekilde yazılmıştır?

A) Tüm a ve b sayıları için a + b = b + a.
B) Bir x sayısı, a > 0 olacak şekilde seçilmiştir.
C) Her x için x² ≥ 0.
D) ∀a, b ∈ ℝ, a + b = b + a.
E) a ve b için a * b ≥ 0.

Çözüm:
Sembolik dilde “her” ifadesi ∀ ile, gerçek sayılar kümesi ise ℝ ile gösterilir. Doğru ifade D

3. Soru: Gerçek sayılar kümesinde aşağıdaki özelliklerden hangisi yanlıştır?

A) ∀x ∈ ℝ için x + 0 = x, bu özellik birim eleman özelliğidir.
B) x ∈ ℝ, y ∈ ℝ için x + y = y + x, bu özellik değişme özelliğidir.
C) x ∈ ℝ için x + (-x) = 0, bu özellik ters eleman özelliğidir.
D) Herhangi bir a ve b ∈ ℝ için (a + b)² = a² + b², bu bir özdeşliktir.
E) x, y, z ∈ ℝ için (x + y) + z = x + (y + z), bu birleşme özelliğidir.

Çözüm:
(D) seçeneği yanlıştır çünkü (a + b)² = a² + 2ab + b²’dir. Doğru cevap D

4. Soru:
Öğretmen, sembolik dili kullanarak “Tüm gerçek sayılar için karesi sıfırdan büyük olan sayılar pozitiftir” ifadesini sembolik dilde yazar. Aşağıdakilerden hangisi öğretmenin ifadesini doğru şekilde ifade etmektedir?

A) ∀x ∈ ℝ, x² ≥ 0
B) ∃x ∈ ℝ, x² > 0
C) ∀x ∈ ℝ, x² > 0 ise x > 0
D) ∃x ∈ ℝ, x² < 0
E) ∀x ∈ ℝ, x² < 0

Çözüm:
Doğru sembolik ifade, “Tüm x ∈ ℝ için, eğer x² > 0 ise x > 0” şeklinde olmalıdır. Bu ifadeyi en iyi şekilde ifade eden seçenek C