Mutlak değer fonksiyonları, matematikte özellikle fonksiyonlar konusunun önemli bir parçasını oluşturur. Bir gerçel sayının mutlak değeri, sayının sıfırdan olan uzaklığını ifade eder ve bu uzaklık her zaman pozitif veya sıfırdır. Mutlak değer fonksiyonları, f(x) = |x| gibi basit bir yapıdan, f(x) = ± |ax + b| ± c gibi daha karmaşık yapılarla ifade edilebilir. Bu fonksiyonlar, matematiksel modellerde, özellikle değişimlerin ve mutlak mesafelerin analizinde önemli bir rol oynar.

Gerçek Sayılarda Tanımlı Mutlak Değer Fonksiyonları ve Nitel Özellikleri Test Çöz

9. Sınıf Gerçek Sayılarda Tanımlı Mutlak Değer Fonksiyonları ve Nitel Özellikleri Ders Notu

Örnek:

Örnek:

Dikkat: Gerçek sayılarda tanımlı |f(x)| fonksiyonunun grafiği çizilirken önce f fonksiyonunun grafiği çizilir. Daha sonra f fonksiyonunun işaretinin negatif olduğu kısım x eksenine göre yansıması alınarak |f(x)|’in grafiği çizilmiş olur.

Örnek:

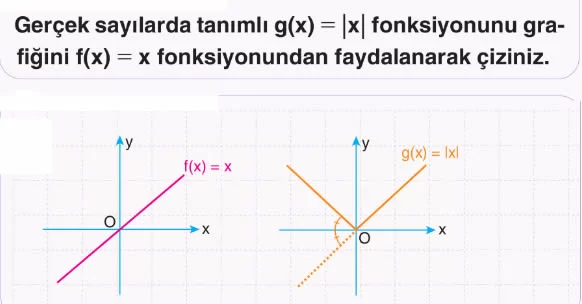
Örnek: Gerçek sayılarda tanımlı f(x) = |x| fonksiyonunun grafiğinin eksenleri kestiği noktaları bulunuz.

• x = 0 için f(0) = |0| = 0
  f fonksiyonu x eksenini (0, 0) noktasında keser.
• f(x) = |x| = 0 ⇒ x = 0
  f fonksiyonu y eksenini de (0, 0) noktasında keser.

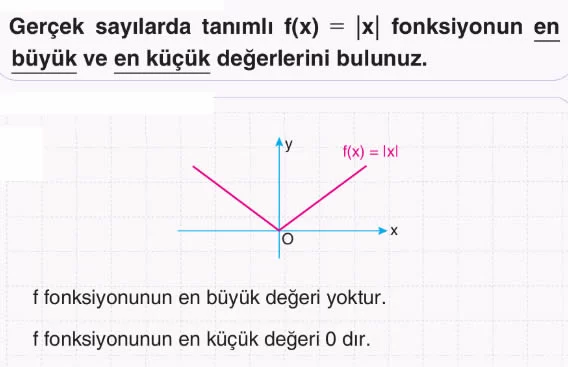
Örnek: Gerçek sayılarda tanımlı f(x) = |x| fonksiyonunun pozitif ve negatif olduğu aralıkları bulunuz.

• ∀ x ∈ ℝ için |x| ≥ 0 olduğundan f fonksiyonunun negatif olduğu aralık yoktur.
• f fonksiyonunun pozitif olduğu aralık: ℝ − {0}’dır.

Örnek:

Örnek:

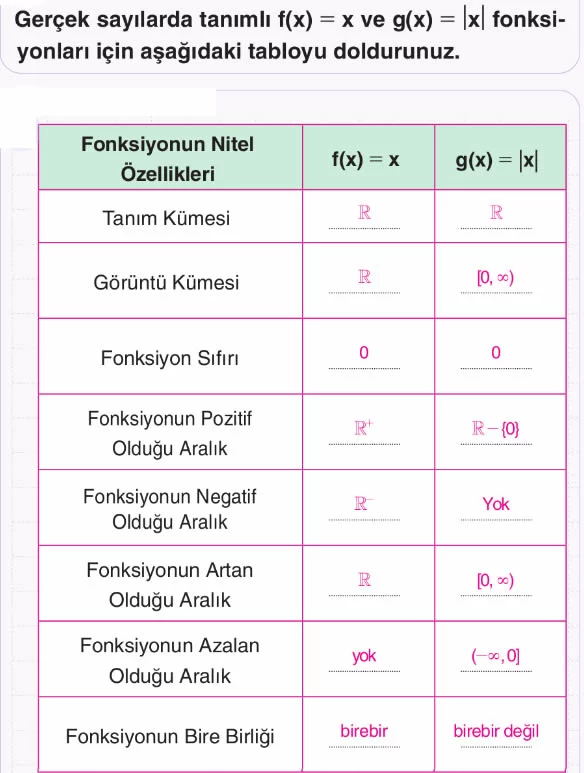
Örnek: Gerçek sayılarda tanımlı f(x) = -|x| fonksiyonunun tanım ve görüntü kümesini bulunuz.

• Tanım kümesi: ℝ’dir.
• ∀ x ∈ ℝ için |x| ≥ 0 iken -|x| ≤ 0’dır.
• f’nin görüntü kümesi: (-∞, 0]’dır.

Örnek:

Örnek: Gerçek sayılarda tanımlı f(x) = -|x| fonksiyonu bire bir midir?

• f(2) = -|2| = -2
• f(-2) = -|-2| = -2

2 ≠ -2 iken f(2) = f(-2) olduğu için f fonksiyonu bire bir değildir.

Örnek:

Örnek:

Örnek:

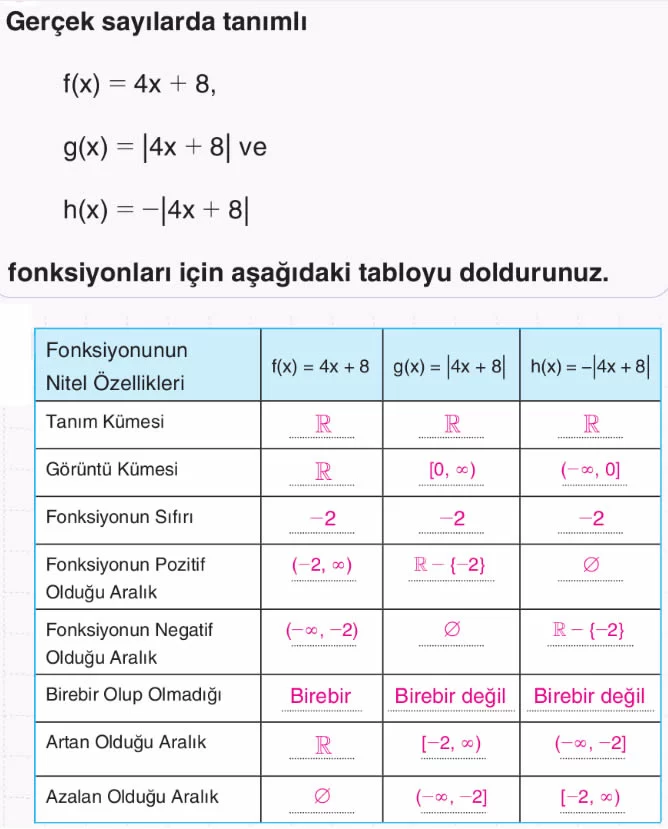
Gerçek Sayılarda Tanımlı f(x) = ± |ax + b| ± c Biçimindeki Mutlak Değer Fonksiyonlarının Grafikleri

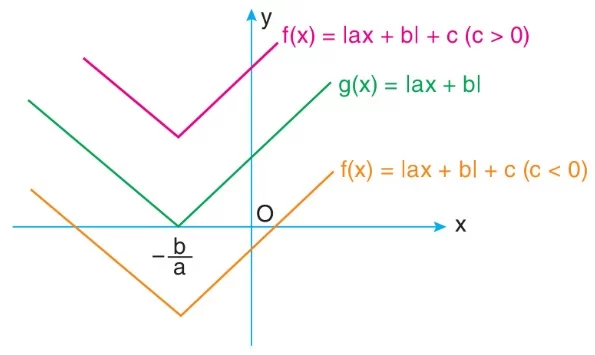
Gerçek sayılarda tanımlı f(x) = |ax + b| + c (c ∈ R) biçimindeki fonksiyonların grafikleri, gerçek sayılarda tanımlı g(x) = |ax + b| fonksiyonlarının grafiklerinden faydalanılarak çizilebilir.

f fonksiyonunun grafiği;

• c ∈ R⁺ ise g fonksiyonunun grafiği y ekseni boyunca pozitif yönde c birim ötelenerek,
• c ∈ R⁻ ise g fonksiyonunun grafiği y ekseni boyunca negatif yönde |c| birim ötelenerek elde edilir.

Eğer f fonksiyonu f(x) = – |ax + b| + c biçiminde ise g fonksiyonunun grafiği y ekseni boyunca negatif yönde simetri alınarak ve aynı işlemler yapılarak f fonksiyonunun grafiği çizilir.

Örnek:

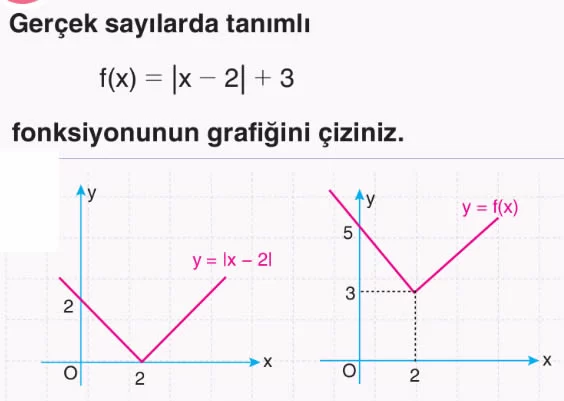
Örnek:

---

Çözümlü Örnek Test Soruları

Soru 1:

Bir öğrenci, f(x) = |x – 4| + 2 fonksiyonunun grafiğini çizmek istiyor. Grafik hakkında şu bilgileri not alıyor:

1. Fonksiyonun tepe noktası (4, 2) noktasında bulunuyor.
2. Grafiğin sol tarafında azalan, sağ tarafında artan bir çizgi var.
3. Grafikte fonksiyonun değeri hiçbir zaman 2’den küçük olmuyor.

Buna göre, bu fonksiyonun x eksenini kestiği değerler aşağıdakilerden hangisidir?

A) 3 ve 5
B) -4 ve 4
C) 4 ve 6
D) 2 ve 6
E) Fonksiyon x eksenini kesmez

Cevap: E
Çözüm: Mutlak değer fonksiyonlarında f(x) = |x – 4| + 2 grafiğinin en küçük değeri 2’dir. Dolayısıyla, grafik hiçbir zaman 0 değerini almaz ve x eksenini kesmez.

Soru 2:

Bir eğitmen, g(x) = |x| + |x – 2| fonksiyonunun grafiği üzerine bir soru hazırlıyor. Soruda, bu fonksiyonun minimum değeri hakkında bilgi soruluyor. Öğrenciler minimum değeri bulmak için şu adımları izliyor:

1. Fonksiyonun iki farklı mutlak değer olduğu için kritik noktalarını belirliyor.
2. x = 0 ve x = 2 noktalarında fonksiyonun değerlerini hesaplıyor.
3. Bu kritik değerler arasında grafiğin en düşük noktasını buluyor.

Fonksiyonun minimum değeri nedir?

A) 0
B) 1
C) 2
D) 3
E) 4

Cevap: C
Çözüm: Fonksiyonda g(x) = |x| + |x – 2|. Kritik noktalar x = 0 ve x = 2’dir.
g(0) = |0| + |0 – 2| = 0 + 2 = 2
g(2) = |2| + |2 – 2| = 2 + 0 = 2
Fonksiyonun minimum değeri 2’dir.

Soru 3:

Bir fonksiyon f(x) = |2x – 6| + 3 olarak tanımlanmıştır. Fonksiyonun en küçük değeri nedir?

A) 3
B) 6
C) 9
D) 0
E) 4

Cevap: A
Çözüm: Mutlak değerli fonksiyonun minimum değeri, mutlak değerin içerisi sıfır olduğunda elde edilir.
2x – 6 = 0 → x = 3
f(3) = |2 * 3 – 6| + 3 = |0| + 3 = 3
Fonksiyonun minimum değeri 3’tür.

Soru 4:

Aşağıdaki fonksiyonlardan hangisinin grafiği x eksenini 2 ve -2 noktalarında keser?

A) f(x) = |x – 2| + |x + 2|
B) f(x) = |x – 2| – |x + 2|
C) f(x) = |x| – 2
D) f(x) = |x – 2|
E) f(x) = |x + 2|

Cevap: B
Çözüm: f(x) = |x| – 2 fonksiyonunda x eksenini kesen noktaları bulmak için f(x) = 0 çözülür.
|x| – 2 = 0
|x| = 2
x = -2 ve x = 2
Fonksiyon x eksenini bu noktalarda keser.