Gerçek Sayılarda Tanımlı Doğrusal Fonksiyonlar ve Nitel Özellikleri 9. Sınıf Matematik (Yeni Müfredat)
Gerçek sayılarda tanımlı doğrusal fonksiyonlar, matematikte önemli bir yer tutar ve bu fonksiyonlar birçok uygulama alanında kullanılır. 9. sınıf matematik derslerinde doğrusal fonksiyonlar ve bu fonksiyonların nitel özellikleri, öğrencilerin matematiksel düşünme becerilerini geliştirmek için kritik bir konudur. Doğrusal fonksiyonlar, genellikle “y eşittir mx artı b” şeklinde ifade edilir. Burada “m” eğimi, “b” ise fonksiyonun y eksenini kestiği noktayı gösterir. Bu ders kapsamında, özellikle “f(x) eşittir x” şeklinde tanımlı doğrusal referans fonksiyon ve bu fonksiyonun genel bir formu olan “g(x) eşittir a çarpı f(x artı eksi r) artı eksi k” şeklinde tanımlı doğrusal fonksiyonlar incelenecektir. Bu doğrusal fonksiyonların grafiksel analizleri, eğim, kaydırma, yansıma ve gerilme gibi temel nitel özellikleri üzerinde durulacaktır.
9. Sınıf Gerçek Sayılarda Tanımlı Doğrusal Fonksiyonlar ve Nitel Özellikleri Testleri
9. Sınıf Gerçek Sayılarda Tanımlı Doğrusal Fonksiyonlar ve Nitel Özellikleri Konu Anlatımları
Gerçek Sayılarda f(x) = x Şeklinde Tanımlı Doğrusal Referans Fonksiyon
-
Gerçek sayılarda tanımlı f(x) = x biçimindeki f fonksiyonu doğrusal fonksiyondur.
-
f(x) = x fonksiyonunda x, tüm gerçek sayı değerlerini alabilir.
Bu sebeple f fonksiyonunun en geniş tanım kümesi gerçek sayılardır.
f fonksiyonu, x’in aldığı tüm gerçek sayı değerlerini kendisi ile eşleştirir. Bu sebeple görüntü kümesi gerçek sayılardır.
Buradan, y = f(x) = x fonksiyonu f : R → R biçiminde tanımlanır.
-
f(x) = x referans fonksiyonu olarak ifade edilir.
f(x) = x aynı zamanda birim fonksiyondur.
f(1) = 1, f(3) = 3, f(-7) = -7, …
-
f(x) = x fonksiyonunun dik koordinat düzleminde grafiği aşağıdaki gibidir.
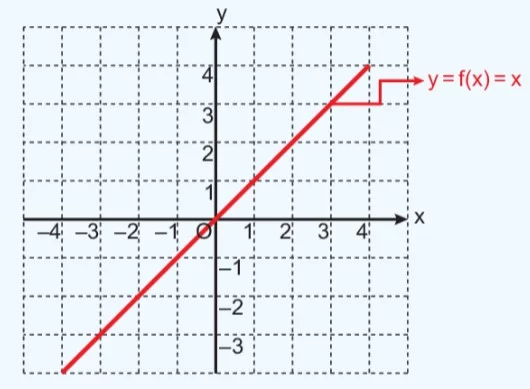
- a ≠ 0, a, b ∈ ℝ olmak üzere, y = ax + b denkleminin grafiği koordinat sisteminde bir doğru belirtir.
- f(x) = ax + b biçimindeki dönüşümlere doğrusal fonksiyonlar denir.
- a ve b sıfırdan farklı ise doğrusal fonksiyon grafiği orijinden geçmez ve eksenlere paralel değildir. Fonksiyon yapısı ilerideki bölümlerde detaylı biçimde incelenecek.
- f(x) = ax biçimindeki doğrusal fonksiyonların grafikleri orijinden geçer.
- Özel olarak, f(x) = x fonksiyonuna doğrusal referans fonksiyonu adı verilir.
Not: f(x) = x doğrusal referans fonksiyonunun diğer adı birim fonksiyondur.
Örnek: f(x) = 3x + 5 doğrusal fonksiyonun cebirsel temsilidir.
| x | 1 | 2 | 3 |
|---|---|---|---|
| f(x) | f(1) = 3·1 + 5 = 8 | f(2) = 3·2 + 5 = 11 | f(3) = 3·3 + 5 = 14 |
- Tablosu, f(x) = 3x + 5 fonksiyonunun x bağımsız değişkenine bağlı değer tablosudur.
Bu bölümde f(x) = x doğrusal referans fonksiyonunu kullanarak fonksiyon özelliklerini inceleyeceğiz.
Örnek: Gerçek sayılarda tanımlı f(x) = 5x – 6 doğrusal fonksiyonu için f(1) ve f(2) değerleri toplamı kaçtır?
Çözüm:
- f(1) değerini bulalım:
f(1) = 5 . 1 – 6 = 5 – 6 = -1 - f(2) değerini bulalım:
f(2) = 5 . 2 – 6 = 10 – 6 = 4 - f(1) ve f(2) değerlerinin toplamı:
-1 + 4 = 3
Örnek: f(x) = x doğrusal referans fonksiyonu için f(6) değeri kaçtır?
Çözüm: f(6) = 6
Örnek: f(x) = x doğrusal referans fonksiyonu için f(x) = 11 eşitliğini sağlayan x değeri kaçtır?
Çözüm: f(x) = x = 11
Bu durumda x = 11 olur.
Örnek: Gerçek sayılarda tanımlı f ve g fonksiyonlarının cebirsel temsilleri:
f(x) = 7x + 1
g(x) = 2 – 4x
şeklinde verilmiştir.
| x | -1 |
|---|---|
| f(x) | a |
| g(x) | b |
Fonksiyonların değer tablosuna göre a + b toplamı kaçtır?
Çözüm:
- f(-1) değerini bulalım:
f(-1) = 7 × (-1) + 1 = -7 + 1 = -6
Bu durumda a = -6 - g(-1) değerini bulalım:
g(-1) = 2 – 4 × (-1) = 2 + 4 = 6
Bu durumda b = 6 - a + b toplamı:
a + b = -6 + 6 = 0
Cevap: 0
f(x) = y şeklindeki fonksiyonlarda x elemanına bağımsız (serbest) değişken, f(x) elemanına bağımlı değişken denir.
Örnek: Saatte 5 km hızla giden bir köpeğin gittiği yolun zamana bağlı değişim grafiği aşağıdaki gibidir.
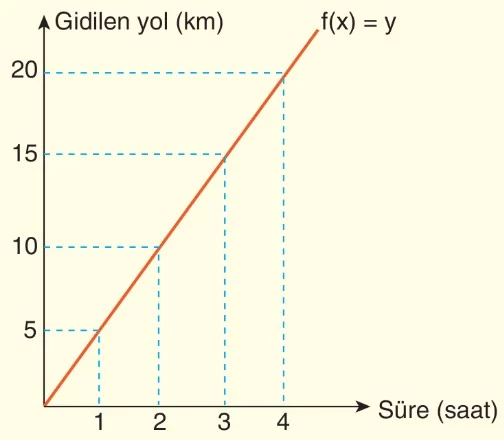
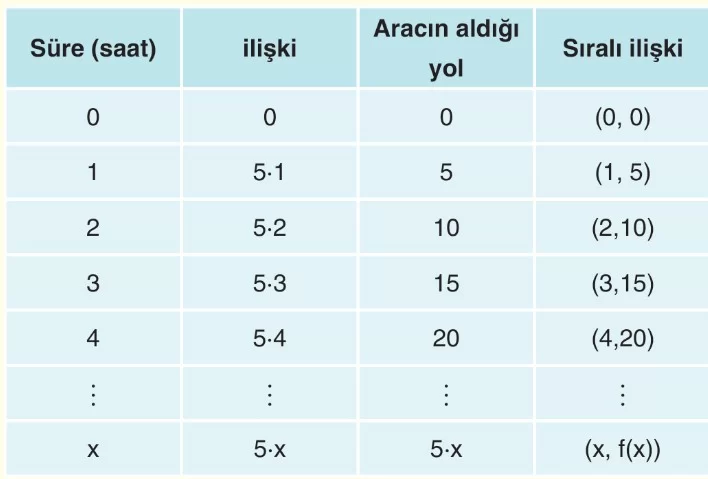
Buna göre bu köpeğin gittiği yolun zamana bağlı değişimini tablo ve denkleme göre gösteriniz.
Çözüm: Verilen grafikte x değişkenine bağlı olarak y değişmektedir. Buna göre x bağımsız değişkendir, f(x) bağımlı değişkendir.
Tanım ve Değer Kümesi
- Bir fonksiyonda bağımsız değişkenin alabileceği tüm değerler kümesi, fonksiyonun tanım kümesi olarak adlandırılır. Bağımsız değişkenin alabileceği tüm değerlere karşılık bağımlı değişkenin alabileceği tüm değerler kümesi, görüntü kümesi olarak adlandırılır.
- Cebirsel temsili f(x) = x olan fonksiyonunda x, tüm gerçek sayı değerlerini alabilir. Bu sebeple fonksiyonun en geniş tanım kümesi gerçek sayılardır. f(x) = x fonksiyonu, x‘in aldığı tüm gerçek sayı değerini kendisi ile eşleştirir. Bu sebeple f fonksiyonunun görüntü kümesi gerçek sayılardır.
- Buradan f fonksiyonu, f: R → R biçiminde tanımlanabilir. Buna f, R’de tanımlıdır da denilebilir.
Görüntü kümesi kavramını bir örnekle açıklayalım.
Örnek:
A = {1, 2, 3}, B = {5, 7, 9, 10} ve f: A → B,
f(x) = 2x + 3 fonksiyonu f = {(1, 5), (2, 7), (3, 9)}
şeklinde tanımlansın.
f(1) = 5, f(2) = 7, f(3) = 9 olduğundan
f(A) = {5, 7, 9}’dur.
A’ya Tanım Kümesi
B’ye Değer Kümesi
f(A)’ya Görüntü Kümesi denir.
NOT: A’dan B’ye tanımlanan bir ifadenin fonksiyon olabilmesi için:
- A’da eşlenmeyen (boşta kalan) eleman bulunmamalıdır.
- A kümesinin bir elemanı, B kümesinin birden fazla elemanı ile eşlenmemelidir.
Örnek: f = {(1, 7), (3, 6), (5, 9)} şeklinde tanımlanan fonksiyon için f(1) + f(5) + f(3) toplamı kaçtır?
Çözüm: f(1) = 7, f(5) = 9, f(3) = 6
Toplam: 7 + 9 + 6 = 22
Örnek: f = {(1, 9), (2, 10), (3, 11), (4, 15)} ifadesi bir fonksiyon olduğuna göre tanım kümesini bulunuz.
Çözüm: Tanım kümesi, fonksiyonun ilk elemanlarını içerir:
{1, 2, 3, 4}
Örnek: A = {-1, 0, 1} ve f : A -> R, f(x) = x + 2 olduğuna göre, f(A) görüntü kümesini bulunuz.
Çözüm: f(-1) = -1 + 2 = 1
f(0) = 0 + 2 = 2
f(1) = 1 + 2 = 3
Görüntü kümesi: {1, 2, 3}
Örnek: A’dan B’ye tanımlanmış f fonksiyonu f = {(-1, 4), (-2, 6), (-3, 5)} olduğuna göre, f fonksiyonunun görüntü kümesini bulunuz.
Çözüm: Görüntü kümesi, fonksiyonun ikinci elemanlarını içerir:
{4, 6, 5}
Doğrusal Fonksiyonlarda Eğim

Örnek:

Fonksiyonun Sıfırı
a ≠ 0, a ve b ∈ R olmak üzere, f : R → R, f(x) = ax + b ifadesine doğrusal fonksiyon adı verilmiştir. Doğrusal fonksiyonların grafikleri koordinat sisteminde bir doğru belirtir.Bu doğrunun x eksenini kestiği noktaya yani f(x) = 0 eşitliğini sağlayan x değerine f fonksiyonunun sıfırı denir.
Örnek: f(x) = 2x – 6 fonksiyonu için f(x) = 0,
2x – 6 = 0, x = 3 elde edilir.
x = 3’e f(x) fonksiyonunun sıfırı denir.
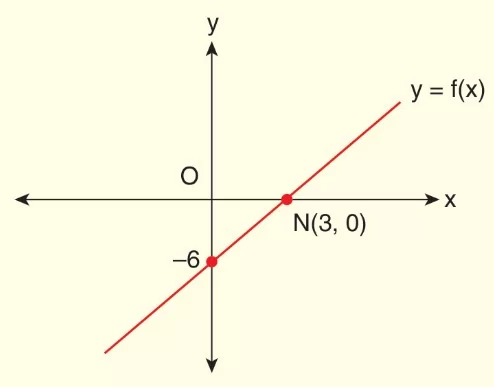
A(3, 0) noktası doğrunun x eksenini kestiği noktadır.
Not: f(x) = b biçimindeki doğrusal fonksiyonlar x eksenini kesmez. Dolayısıyla sıfırı yoktur.
Not: Ayrıca fonksiyonun y eksenini kestiği yeri bulmak için de x yerine 0 yazılır.
Örnek: Aşağıda verilen fonksiyonların sıfırlarını bulunuz.
a) f(x) = x
b) f(x) = 4x + 12
c) f(x) = 15 – 3x
d) f(x) = 7
Çözüm:
a) f(x) = x için sıfır değeri, x = 0’dır.
b) f(x) = 4x + 12 fonksiyonunun sıfırını bulmak için f(x) = 0 denklemini çözelim:
4x + 12 = 0
4x = -12
x = -3
c) f(x) = 15 – 3x fonksiyonunun sıfırını bulmak için f(x) = 0 denklemini çözelim:
15 – 3x = 0
-3x = -15
x = 5
d) f(x) = 7 fonksiyonu sabit bir fonksiyon olduğu için sıfırı yoktur.
Örnek: Uygun aralıklarla tanımlanmış
f(x) = 20 – 4x ve g(x) = (1/2)x – 3
fonksiyonlarının sıfırlarının toplamı kaçtır?
Çözüm:
- f(x) = 20 – 4x için sıfırı bulalım:
20 – 4x = 0
-4x = -20
x = 5 - g(x) = (1/2)x – 3 için sıfırı bulalım:
(1/2)x – 3 = 0
(1/2)x = 3
x = 6
Sıfırların toplamı: 5 + 6 = 11
Örnek: f : R → R, f(x) = (3/2)x – 6 fonksiyonu x eksenini hangi noktada keser?
Çözüm:
x eksenini kestiği noktayı bulmak için f(x) = 0 yapalım:
(3/2)x – 6 = 0
(3/2)x = 6
x = 4
Fonksiyon x eksenini x = 4 noktasında keser.
Artan – Azalan ve Sabit Fonksiyonlar
f(x) = x fonksiyonunun grafiği verilmiştir.
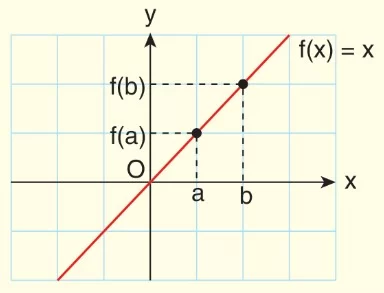
I. Her a, b ∈ R için
a < b ise f(a) < f(b) olur.
f, gerçek sayılarda ARTAN‘dır.
II. Her a, b ∈ R için
a < b ise f(a) > f(b) olur.
f, gerçek sayılarda AZALAN‘dır.
III. Her a, b ∈ R için
a = b ise f(a) = f(b) olur.
f, gerçek sayılarda SABİT‘tir.
Örnek:
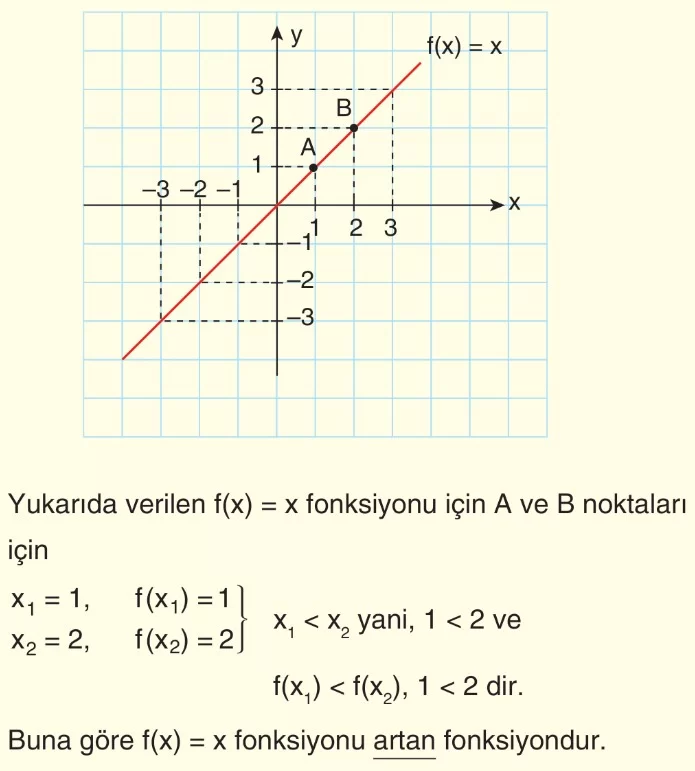
Örnek: Aşağıda f : R → R fonksiyonunun grafiği verilmiştir.
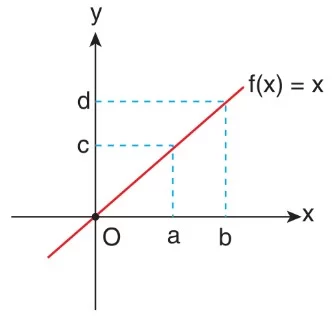
Buna göre aşağıdaki ifadeler verilmiştir:
I. f(a) = c
II. f(b) = d
III. 0 < a < b
IV. 0 < c < d
V. f(b) < f(c)
Bu ifadelerden hangileri yanlıştır?
Çözüm: Grafikteki fonksiyon f(x) = x olduğuna göre,
bu fonksiyon doğrusal bir fonksiyon olup her x değeri için f(x) = x olur. Bu durumda:
- I. f(a) = c : Doğru, çünkü grafikte a ile c eşleşmiştir. Ayrıca f(a) = a olduğundan a = c dir.
- II. f(b) = d : Doğru, çünkü grafikte b ile d eşleşmiştir. Ayrıca f(b) = b olduğundan b = d dir.
- III. 0 < a < b : Doğru, grafikte 0 ile b arasında a konumlanmıştır.
- IV. 0 < c < d : Doğru, grafikte 0 ile d arasında c konumlanmıştır.
- V. f(b) < f(c) : Yanlış, çünkü f(x) = x olduğundan f(b) = b ve f(c) = c olur. Burada b < c ve b = d olduğundan d < c olur. Bu ifade yanlıştır.
Yanıt: Yalnız V yanlıştır.
Bir Fonksiyonun Maksimum ve Minimum Değerleri
- a, b ∈ R ve f fonksiyonu [a, b] aralığında tanımlı olsun.
∀ x ∈ [a, b] için f(x) ≤ f(m) şartını sağlayan f(m) değerine fonksiyonun maksimum değeri,
(m, f(m)) noktasına f fonksiyonunun maksimum noktası denir.- ∀ x ∈ [a, b] için f(x) ≥ f(n) şartını sağlayan f(n) değerine fonksiyonun minimum değeri,
(n, f(n)) noktasına f fonksiyonunun minimum noktası denir.
Örnek:
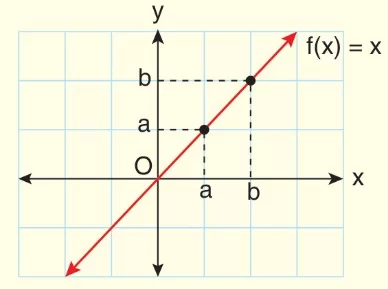
Şekildeki R → R tanımlı f(x) = x fonksiyonunun maksimum ve minimum değerleri yoktur.
Not: Fonksiyonun tanım aralığı değiştikçe maksimum ve minimum değeri değişebilir.
Örnek:
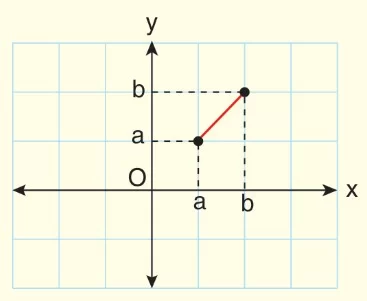
f: [a, b] → [a, b] tanımlı f(x) = x fonksiyonu için,
Maksimum değer: b, maksimum nokta: (b, b)
Minimum değer: a, minimum nokta (a, a)’dır.
Örnek: f : (a, b) → (a, b) tanımlı f(x) = x fonksiyonu verilsin.
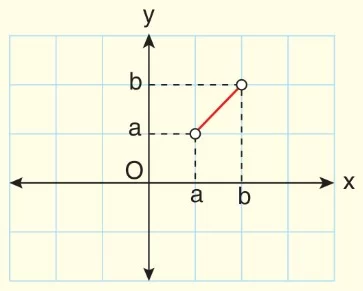
Tanım aralığı açık aralık olduğu için bu fonksiyonun maksimum ve minimum değeri yoktur.
Örnek:

Çözüm: Verilen fonksiyon grafiği üzerinden ifadeleri inceleyelim.
Fonksiyon f : [−3,5]→R şeklinde tanımlıdır ve grafikte f(x) = x doğrusu verilmiştir. Bu doğrusal fonksiyon tanım aralığında [-3, 5] sürekli artış gösterir.
Minimum Değer:
Tanım aralığında x = -3 olduğunda f(x) = -3 olur.
Dolayısıyla minimum değeri -3’tür.
Maksimum Değer:
Tanım aralığında x = 5 olduğunda f(x) = 5 olur. Dolayısıyla maksimum değeri 5’tir.
Artan Fonksiyon:
f(x) = x doğrusal bir fonksiyon olup, pozitif eğimlidir ve tüm tanım aralığında artan bir fonksiyondur.
Sonuç:
- I. Minimum değeri -3’tür.
- II. Maksimum değeri 5’tir.
- III. Artan fonksiyondur.
Doğru Cevap: I, II ve III ifadeleri doğrudur.
Bir Fonksiyonun Pozitif ve Negatif Değerleri (İşaret Tablosu)
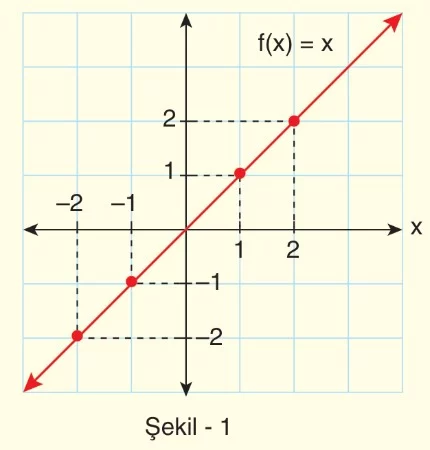
- f : R → R tanımlı f(x) = x fonksiyonunun grafiği incelendiğinde, y = x doğrusunun bir kısmı x ekseninin üst kısmında kalır, bunu sağlayan x değerleri (0, ∞) aralığındadır. Bu durumu x > 0 için f(x) > 0, f(x) pozitif değerler alır olarak ifade ederiz.
- Grafiğin bir kısmı ise x ekseninin altında kalır, bunu sağlayan x değerleri (-∞, 0) aralığındadır. Bu durumu x < 0 için f(x) < 0, f(x) negatif değerler alır olarak ifade ederiz.
- Bunun için fonksiyonu 0 yapan değer yani fonksiyonun sıfırı bulunur. Bulunan değer tabloya yerleştirilir. Bu değerin sağında ve solunda hangi değerleri aldığına bakarak işaret tablosu yapılır.
- Şekil – 1 incelendiğinde x > 0 iken f(x) in pozitif değerler aldığı, x < 0 iken f(x) in negatif değerler aldığı görülür.
f fonksiyonunun sıfırına göre işaret incelemesi aşağıdaki gibi yapılabilir.

İşaret tablosuna göre her x ∈ (-∞, 0) için fonksiyonun işaretinin negatif olduğu, her x ∈ (0, ∞) için fonksiyonunun işaretinin pozitif olduğu görülür.
Örnek:
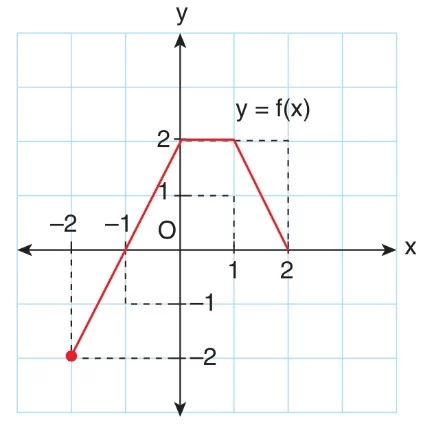
Buna göre, y = f(x) fonksiyonunun pozitif değerler aldığı aralık nedir?
Çözüm: Grafikten görüldüğü üzere, fonksiyon y ekseninin üstünde pozitif değerler almaktadır. Bu pozitif değerler x ekseninde şu aralıklara karşılık gelir:
-1 < x < 2
Sonuç olarak, y = f(x) fonksiyonunun pozitif değer aldığı aralık (-1, 2) aralığıdır.
Örnek:
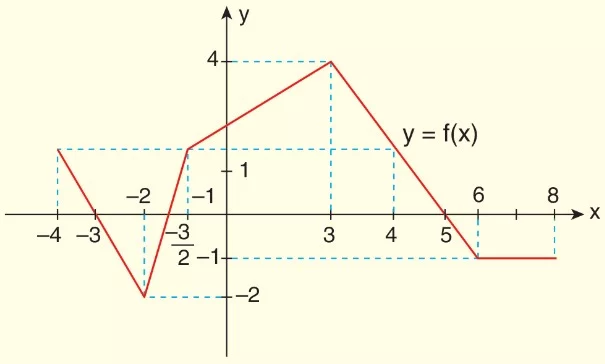
Yukarıda f: [−4, 8] → [−2, 4] grafiği veriliyor.
a) Fonksiyonun verilen aralıktan alabileceği maksimum ve minimum değerleri bulalım.
b) Fonksiyonun işaret tablosunu bulalım.
c) Fonksiyonun sabit olduğu aralığı bulalım.
Fonksiyon tanımlı olduğu aralıklara dikkat edecek olursak,
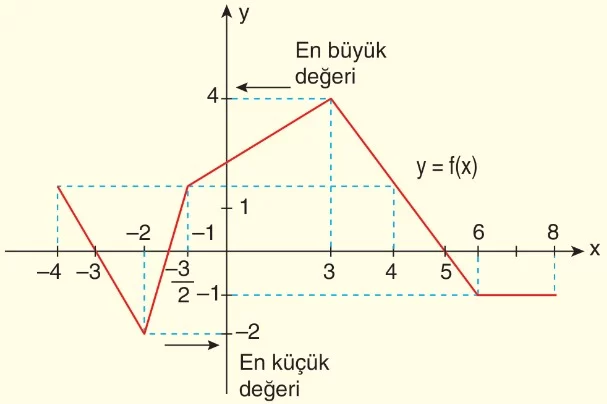
a)
Maksimum değeri = 4
Minimum değeri = -2 olur.
b) Fonksiyonun x eksenini kestiği noktaları bulup tabloya yazalım.
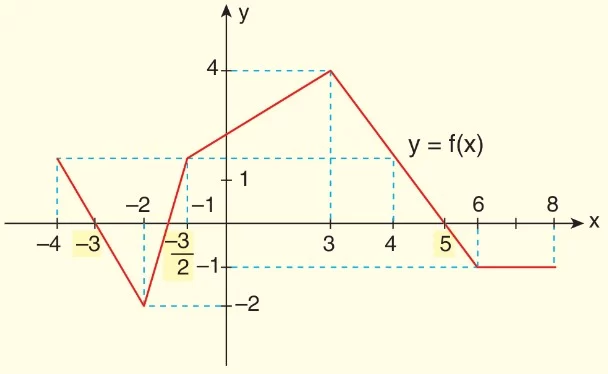
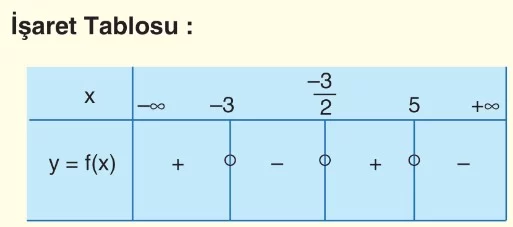
Not: İşaret tablosu, x değerleri için f(x) değerlerinin işaretini gösterir.
c) Fonksiyonun sabit olduğu aralığı grafikte inceleyelim.
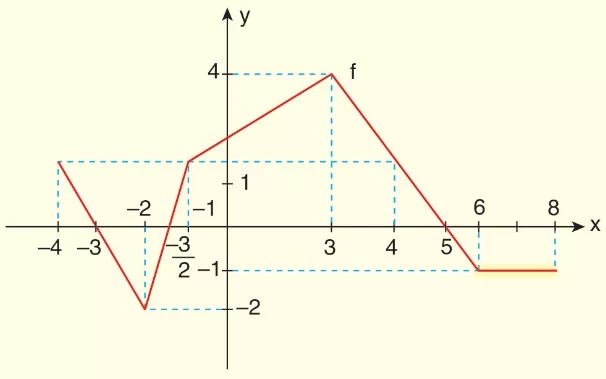
[6, 8] aralığında fonksiyon sabittir.
Bire Bir Fonksiyon
Bir f fonksiyonunda tanım kümesindeki farklı x değerlerine karşılık gelen değerleri birbirinden farklı ise bu fonksiyona bire bir (1-1) fonksiyon denir.
Aşağıda f(x) = x fonksiyonunun grafiği verilmiştir. Gerçek sayılarda tanımlı f fonksiyonunda a ve b, tanım kümesinin herhangi iki elemanı olsun.
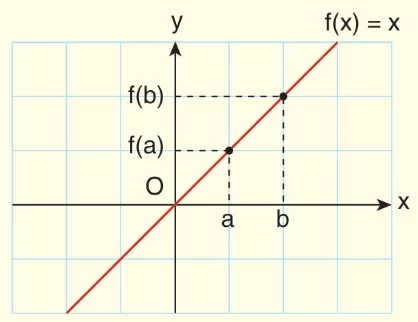
ve b değerleri birbirinden farklı iken ve değerlerinin de birbirinden farklı olduğu, a ve b değerlerinin eşit olması durumunda ve değerlerinin de birbirine eşit olması beklenir.
Not: f: R → R f(x) = x biçimindeki f fonksiyonunda
için ff(a) = a ve f(b) = b olur.
Cebirsel olarak,
a ≠ b ⇒ f(a) ≠ f(b) ve olur.
Bu durumda f, birebir fonksiyondur.
Not: tanımlı tüm doğrusal fonksiyonlar birebirdir.
UYARI: Tanım kümesi, görüntü kümesi, işaretli, artanlığı – azalanlığı, maksimum – minimum noktaları, sıfırı ve birebirliği bir fonksiyonun NİTEL özelliklerindendir.
Grafiği Verilen Fonksiyonun Bire Birliğinin İncelenmesi
x eksenine (tanım kümesine) paralel çizilecek doğruların tamamı grafiği birden fazla noktada kesmiyorsa, fonksiyon bire birdir.
Örnek:
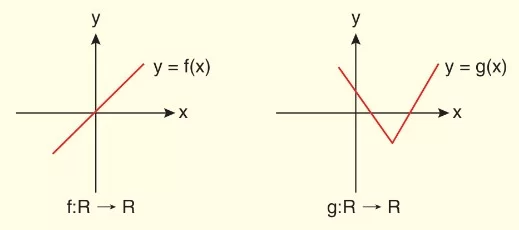
a)
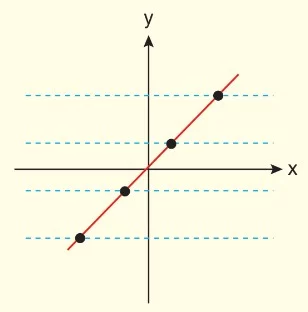
Yatay doğruların hiçbiri f fonksiyonunun grafiğini birden fazla noktada kesmediğinden, f fonksiyonu bire birdir.
b)
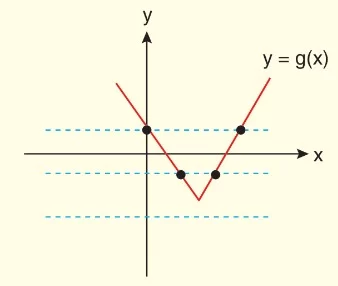
En az bir yatay doğru g fonksiyonunun grafiğini birden fazla noktada kestiğinden, g fonksiyonu bire bir değildir.
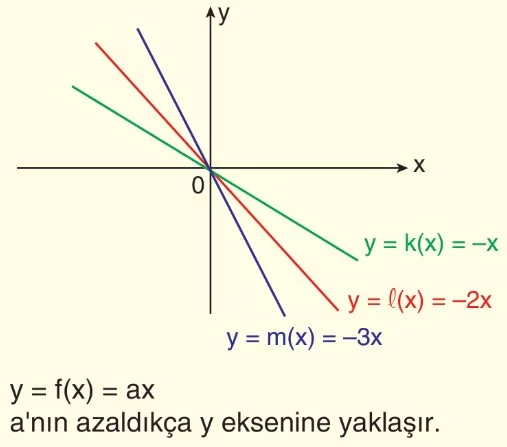
g(x) = a . x Fonksiyonunun Grafiği ve İncelenmesi

g(x) = x + b Fonksiyonunun Grafiği ve İncelenmesi
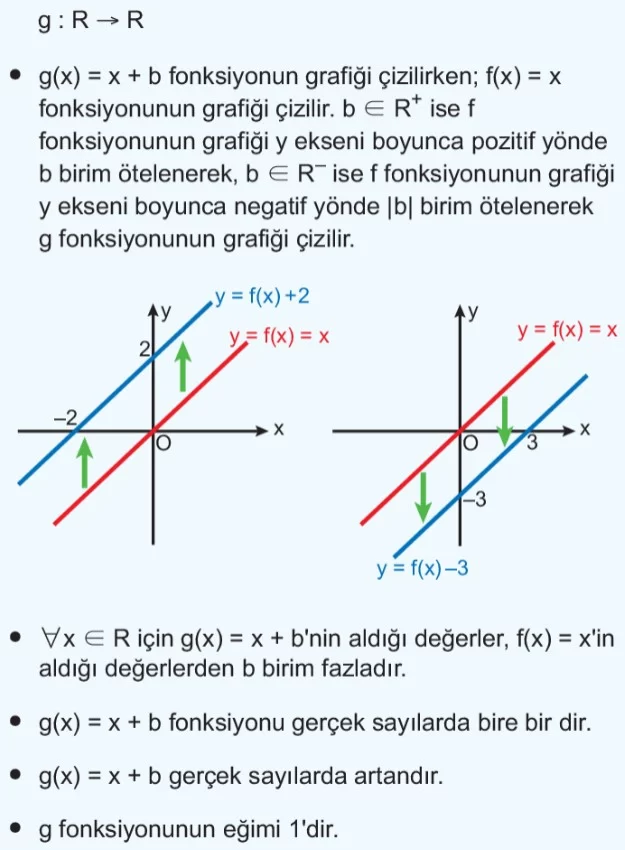
g(x) = ax + b Fonksiyonunun Grafiği ve İncelenmesi

Örnek:

Örnek:

Doğrusal Fonksiyonlarda Artanlık – Azalanlık
f: R → R, f(x) = x şeklinde tanımlı f doğrusal referans fonksiyonu için verilen “Her x1 < x2 için f(x1) < f(x2)“dir. Yani tüm ‘de artandır.
Buradan yola çıkarak:
Önerme:
“Her a > 0 için g: R → R
g(x) = ax + b şeklinde tanımlı g doğrusal fonksiyonu artandır.” önermesini doğrulama ispat metodu ile ispatlayalım.
İspat:
x1 ve x2 birer genel sayı,
x1 < x2 ve a > 0 olsun.
eşitsizliğinin her iki tarafını pozitif bir sayı ile çarparsak yön değişimi olmaz.
a. , her iki tarafa b ekleyelim.
a. oldu. Buradan
g(x1) < g(x2) elde edilir.
Dolayısıyla g artandır.
Sonuç:
a ≠ 0, a, b ∈ R, f: R → R
f(x) = ax + b doğrusal fonksiyonu için:
- a > 0 ⇒ f artandır.
- a < 0 ⇒ f azalandır.
Örnek:
R → R tanımlı
a) f(x) = 4x + 18, artan bir fonksiyondur.
b) g(x) = -3x + 7, azalan bir fonksiyondur.
c) h(x) = 14x, artan bir fonksiyondur.
d) s(x) = -11x, azalan bir fonksiyondur.
e) r(x) = 4, sabit bir fonksiyondur.
Not:Gerçek yaşamda iki değişken arasında bulunan doğrusal ilişki, doğrusal fonksiyonlarla ifade edilebilir. Doğrusal fonksiyonların grafiklerinin koordinat sisteminde bir doğru belirttiğini gösterdik. Fonksiyonların cebirsel ve grafik temsillerinden yararlanarak doğrusal ilişki hakkında çıkarımlar yapılabilir.
Örnek:
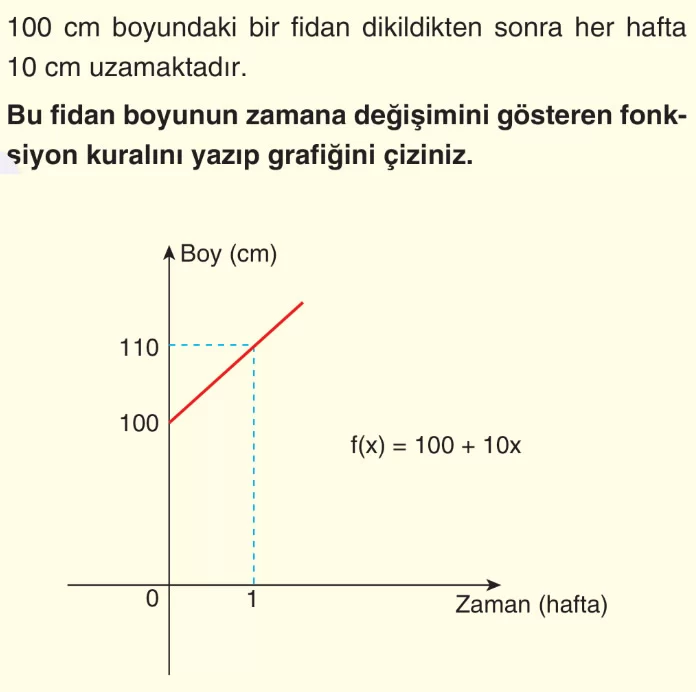
Örnek:
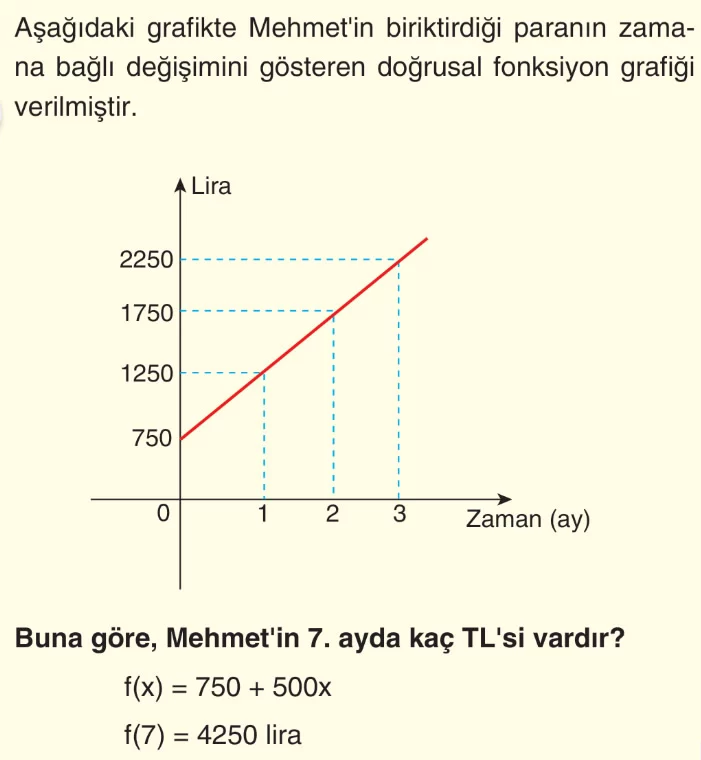
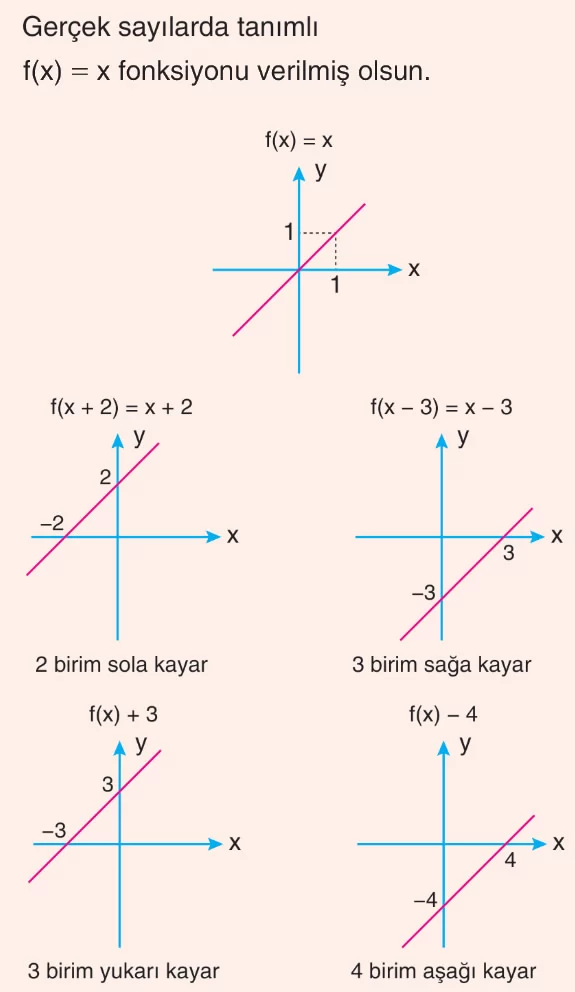
f(x) = a(x ± r) ± k Biçimindeki Doğrusal Fonksiyonlar (Öteleme)
- f(x ± r) ⟶ f(x) fonksiyonu r birim x ekseninde ötelenir.
f(x + 2) ⟶ x ekseninde f(x) fonksiyonu 2 birim sola ötelenir.
f(x – 5) ⟶ x ekseninde f(x) fonksiyonu 5 birim sağa ötelenir. - f(x) ± k ⟶ f(x) fonksiyonu k birim y ekseninde ötelenir.
f(x) + 2 ⟶ f(x) 2 birim yukarı ötelenir.
f(x) – 1 ⟶ f(x) 1 birim aşağı ötelenir.
f(x + 3) – 2 ⟶ f(x) fonksiyonu 3 birim sola, 2 birim aşağı ötelenir. - h(x) = a(x ± r) fonksiyonunun grafiğini elde etmek için
g(x) = x ± r fonksiyonundaki tüm değerler a ile çarpılır. - k(x) = a(x ± r) ± k fonksiyonunun grafiğini elde etmek için
h(x) fonksiyonunun grafiği k birim yukarı ya da aşağı ötelenir.
Bilgi:a, r, k ∈ R ve a ≠ 0 olmak üzere g : R → R,
g : R → R, g(x) = a.f(x ± r) ± k şeklinde tanımlı g doğrusal fonksiyonu için
- g fonksiyonunun en geniş tanım ve görüntü kümesi gerçek sayılardır.
- n ∈ R olmak üzere g fonksiyonunun sıfırı g(0) = n olsun.
- a > 0 veya a < 0 olmak üzere f fonksiyonunun işaret incelemesi aşağıdaki biçimde işaret tablosu yapılabilir.

Örnek:


Fonksiyonların Parçalı Gösterimi
Tanım kümesi farklı kurallarla tanımlı olan fonksiyonlara parçalı tanımlı fonksiyonlar veya parçalı fonksiyonlar denir.
Yani;
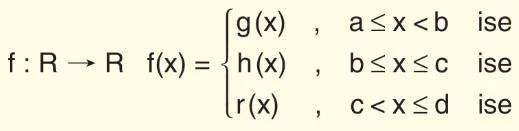
biçiminde tanımlanan f fonksiyonuna parçalı fonksiyon, g(x), h(x), r(x) fonksiyonlarına parçalı fonksiyonun dalları denir.
Örnek:
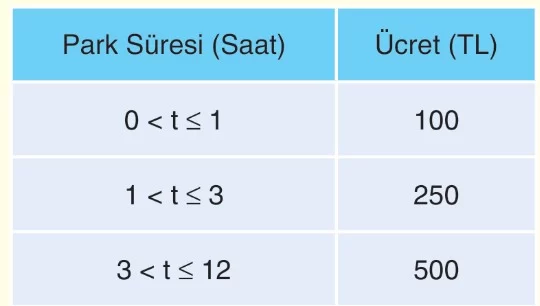
Bir otoparkın ücret tarifesi yukarıdaki gibidir. Buna göre, bu verileri parçalı fonksiyon halinde yazalım.
- t saatte bir aracın otoparkta kaldığı süreyi göstersin, ödeyeceği ücret f(t), birimi lira olsun.
- Park edilen bir araç en fazla 12 saat kalabildiğine göre f’nin tanım kümesi (0, 12] aralığındadır.
Tabloya göre, bir kişi aracı park ettikten sonra:
- 1 saat içinde alırsa 100 TL
Yani, t ∈ (0, 1] için f(t) = 100 - 1 saatten fazla olmak üzere 3 saat içinde alırsa 240 TL
Yani, t ∈ (1, 3] için f(t) = 250 - 3 saatten fazla olmak üzere 12 saat içinde alırsa 500 TL
Yani, t ∈ (3, 12] için f(t) = 500‘dür.

Sabit Fonksiyon
- , f(x) = ax + b ve b ∈ R olmak üzere, a = 0 için f(x) = b şeklinde tanımlı f fonksiyonuna sabit fonksiyon denir. Sabit fonksiyon aynı zamanda doğrusal fonksiyondur. Sabit fonksiyon grafikleri x eksenine paraleldir.
- Sabit fonksiyonların eğimi “0” dır.
Örnek: f(x) = (m – 3).x + 12 sabit fonksiyon olduğuna göre, m değeri kaçtır?
Çözüm: Fonksiyonun sabit fonksiyon olması için x‘in katsayısı sıfır olmalıdır. Yani,
m – 3 = 0
Buradan, m = 3
Örnek: ve g sabit fonksiyonlardır.
3.f(2) + 17 = 2
olduğuna göre g(8) kaçtır?
Çözüm: Sabit fonksiyon oldukları için her x değeri için f(x) = k ve g(x) = m gibi sabit bir değere eşittirler.
1. Denklem:
3.f + 17 = 2
3.f = -15
f = −5
2. Denklem:
(−5) ⋅ g = −20
g = 4
Sonuç olarak, g(8) = 4 olur.
Doğrusal Fonksiyonlar ve Nitel Özellikleri Çözümlü Sorular
Çözümlü Test Soruları
Soru 1:
f(x) = 2x – 5 fonksiyonunun grafiği x-eksenini hangi noktada keser?
A) (0, -5)
B) (5/2, 0)
C) (-5, 0)
D) (0, 5/2)
Çözüm:
x-ekseni kesimi için y=0 yapılır:
0 = 2x – 5 → 2x = 5 → x = 5/2
Doğru cevap B) (5/2, 0).
Soru 2:
Eğimi -3 olan ve y-eksenini (0, 4) noktasında kesen doğrusal fonksiyon aşağıdakilerden hangisidir?
A) f(x) = 3x + 4
B) f(x) = -3x + 4
C) f(x) = -3x – 4
D) f(x) = 4x – 3
Çözüm:
f(x) = ax + b formunda:
-
a = -3 (eğim)
-
b = 4 (y-keseni)
Fonksiyon: f(x) = -3x + 4
Doğru cevap B) f(x) = -3x + 4.
Soru 3:
f(x) = (k-2)x + 3 fonksiyonu sabit fonksiyon olduğuna göre, k kaçtır?
A) -2
B) 0
C) 2
D) 3
Çözüm:
Sabit fonksiyon olması için eğim (a) 0 olmalı:
k – 2 = 0 → k = 2
Doğru cevap C) 2.
Soru 4:
Aşağıdaki fonksiyonlardan hangisinin grafiği orijinden geçer?
A) f(x) = 2x + 1
B) f(x) = -x
C) f(x) = 3x – 2
D) f(x) = 5
Çözüm:
Orijinden geçen fonksiyonlarda b=0 olmalıdır.
B) f(x) = -x (b=0 olduğu için).
Doğru cevap B) f(x) = -x.
Soru 5:
f(x) = ax + b fonksiyonu için f(1) = 5 ve f(-1) = 1 olduğuna göre, a + b kaçtır?
A) 3
B) 4
C) 5
D) 6
Çözüm:
Verilenleri yazalım:
-
a·1 + b = 5 → a + b = 5
-
a·(-1) + b = 1 → -a + b = 1
İki denklemi toplayalım:
(a + b) + (-a + b) = 5 + 1 → 2b = 6 → b = 3
a + 3 = 5 → a = 2
a + b = 2 + 3 = 5
Doğru cevap C) 5.

















