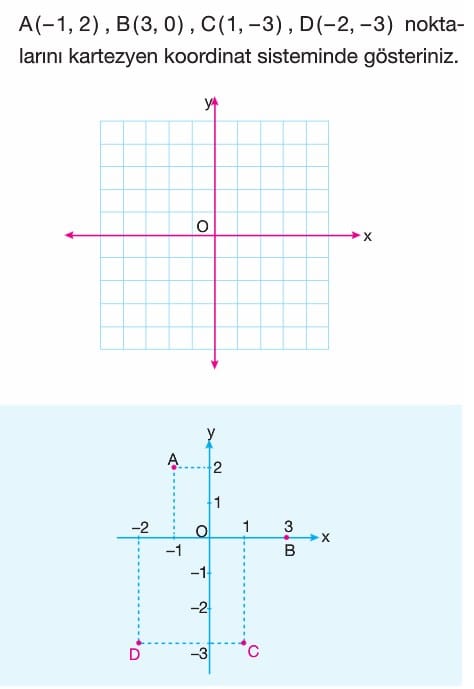
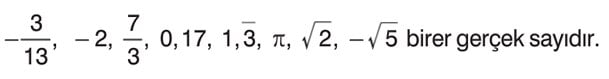Gerçek sayılar (Reel Sayılar) kümesi
Konunun sonunda Çözümlü sorular, online testler ve ders videoları bulunmaktadır.
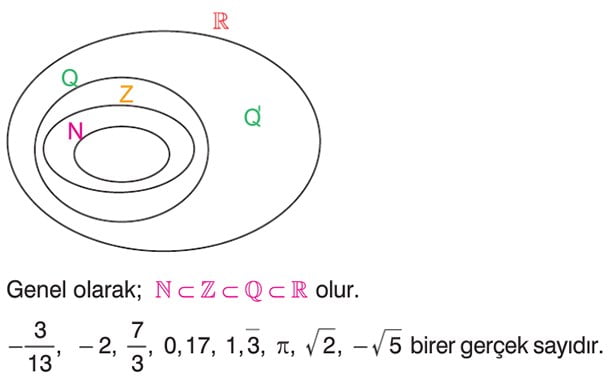
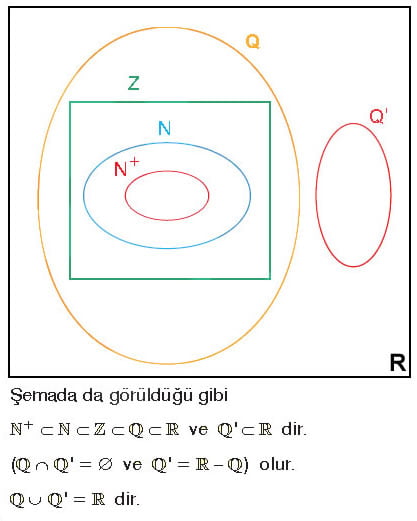
Rasyonel sayılar kümesi ile irrasyonel sayılar kümesinin birleşimi olan kümeye, gerçek (reel) sayılar kümesi denir.
Gerçek sayılar kümesi, R = Q ∪ Q’ ile ifade edilir.
Aşağıdaki Venn şemasını inceleyiniz.
Genel olarak; N ⊂ Z ⊂ Q ⊂ R olur.
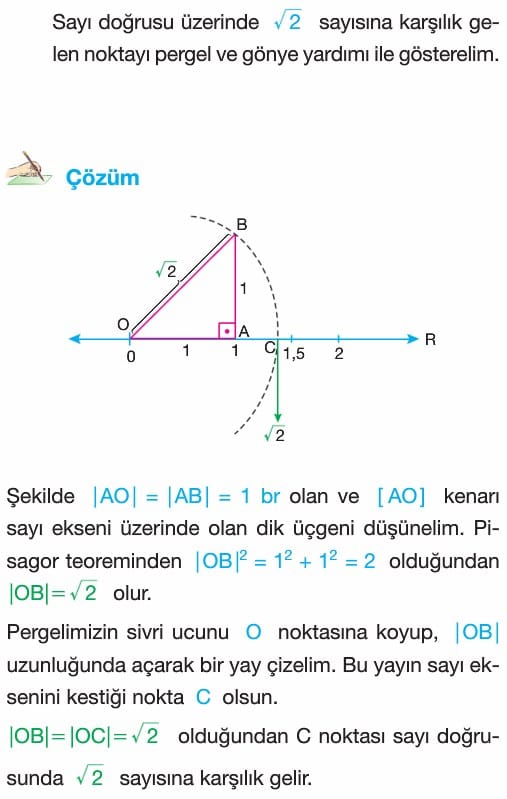
Tüm gerçek sayılar sayı doğrusu üzerine yerleştirildiğinde doğru üzerinde boş nokta kalmaz. Gerçek sayılar kümesi şimdiye kadar işlediğimiz tüm sayı kümelerini içine alan en geniş sayı kümesidir.
Gerçek Sayılar Çözümlü Sorular
Gerçek Sayılar Test 1 Çöz
Gerçek sayılar kümesi konu anlatımı 9. sınıf
Doğal Sayılar: N = {0, 1, 2, 3, ...} kümesinin elemanlarının her birine doğal sayı denir. En küçük doğal sayı sıfırdır.
Sayma Sayıları: Doğal sayılar kümesinden sıfırın çıkartılması ile elde edilen kümeye sayma sayıları kümesi denir ve N+ ile gösterilir. N+ = {1, 2, 3, 4, ...}
Örnek: x ve y doğal sayılar olmak üzere x + y = 7 olduğuna göre 3x + 2y toplamının alabileceği en küçük değeri bulunuz.
Çözüm: 3x + 2y = x + 2x +2y = x + 2.(x + y) = x + 2.7 =x +14
Sonuç x' e bağlı olduğu için x'e alabileceği en küçük değeri vermemiz gerekir. X doğal sayı olduğundan x= 0 seçersek x + 14= 0 + 14 = 14 olur.
Tam Sayılar: Z = {..., -3, -2, -1, 0, 1, 2, 3, ...} kümesinin elemanlarının her birine tam sayı denir. Tam sayılar kümesi, pozitif tam sayılar, negatif tam sayılar ve sıfırın birleşiminden oluşur.
Z+ = {1, 2, 3, 4, ....} ve Z- = {..., -3, -2, -1} olmak üzere Z = Z+∪ Z- ∪ {0}
n ∈ Z olmak üzere 2n+1 genel ifadesiyle belirtilen tam sayılara tek sayı, 2n genel ifadesiyle belirtilen tam sayılara da çift sayı denir.
Ç = {..., -4, -2, 0, 2, 4, 6, ...} ve T= {..., -5, -3, -1, 1, 3, 5, 7, ...}
Her doğal sayı aynı zamanda tam sayı olduğu için doğal sayılar kümesi tam sayılar kümesinin alt kümesidir. (N ⊂ Z )
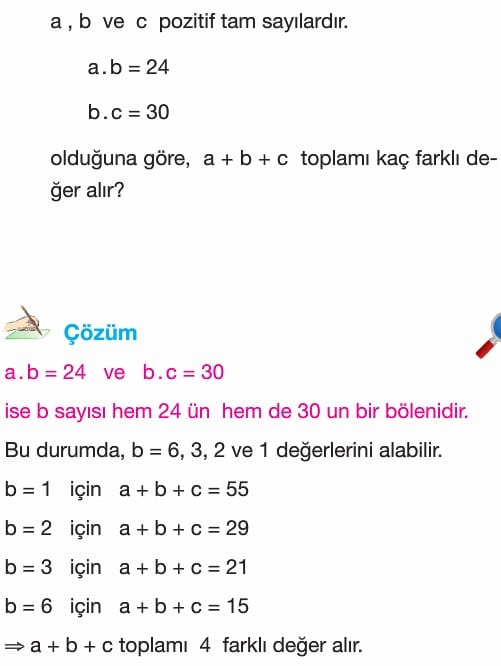
Örnek: a ile b birer tam sayı ve a + b = 14 ise a.b ifadesinin alabileceği en büyük değer kaçtır.
Çözüm: Toplamları sabit olan iki gerçek sayının çarpımlarının en büyük olabilmesi için sayıların bir birine yakın seçilmesi gerekir. Toplamları 14 olan birbirine yakın iki sayı 7 ve 7 dir.
a.b en fazla 7.7'den 49 olur.
Örnek: a ile b birer negatif tam sayıdır. a.b = 7 ve b - c = -3 olduğuna göre, a + b + c toplamını bulunuz.
Çözüm: a.b = 7 olduğuna göre (a = -7 ve b = -1) veya ( a = -1 ve b = -7) dir.
b = -1 ve b - c = -3 için -1 - c = -3, -c = -2 ve c =2 olur. 2 negatif tam sayı olmadığı için c 2 olamaz.
b = -7 ve b - c = -3 için -7 - c = -3, - c = 4 ve c = -4 tür. Buna göre a + b + c = (-1) + (-7) + (-4) = -12 olur.
Rasyonel Sayılar: a, b tam sayı ve b sıfırdan farklı olmak üzere a/b ifadesine rasyonel sayı ya da kesir denir. a ya kesrin payı, b ye de paydası denir. Rasyonel sayılar kümesi Q sembolü ile gösterilir. Rasyonel sayılarda payda sıfır olursa sayı tanımsız olur.
a / b kesrinin pay ve paydasını sıfırdan farklı bir tam sayı ile çarpmaya genişletme, pay ve paydasını sıfırdan farklı bir tam sayı ile bölmeye sadeleştirme denir.
Rasyonel sayılarda toplama ve çıkarma işleminin yapılabilmesi için paydalarının eşit olması gerekir, Eşit değilse genişletme işlemi ile paydalar eşitlenir.
Rasyonel Sayılarda Sıralama:
* Paydalar eşit ise payı büyük olan daha büyüktür.
* Paylar eşit ise paydası küçük olan daha büyüktür.
* Pay ile payda arasındaki farklar eşit ise basit kesirlerde paydası büyük olan büyüktür, bileşik kesirlerde paydası büyük olan küçüktür.
İrrasyonel Sayılar: Rasyonel olmayan gerçek sayılara irrasyonel sayılar denir ve Q' ile gösterilir. İrrasyonel sayılar a/b şeklinde yazılamazlar.
Gerçek (Reel) Sayılar: Rasyonel sayılar kümesi ile irrasyonel sayılar kümesinin birleşiminden oluşan kümeye gerçek sayılar kümesi denir ve R ile gösterilir. R = Q ∪ Q'
Her sayma sayısı bir doğal sayıdır.
Her doğal sayı bir tam sayıdır.
Her tam sayı bir rasyonel sayıdır.
Her rasyonel sayı bir gerçek sayıdır.
Her irrasyonel sayı bir gerçek sayıdır.
Gerçek Sayılarda Toplama İşleminin Özellikleri
Kapalılık Özelliği: İki gerçek sayının toplamı daima gerçek sayı olduğu için gerçek sayılar kümesi toplama işlemine göre kapalıdır.
Değişme Özelliği: a ve b gerçek sayıları için a + b = b + a olduğundan gerçek sayılar kümesinde toplama işleminin değişme özelliği vardır.
Birleşme Özelliği: a, b ve c birer gerçek sayı olmak üzere (a + b) + c = a + (b + c) olduğundan gerçek sayılar kümesinde toplama işleminin birleşme özelliği vardır.
Etkisiz Eleman Özelliği (Birim Eleman): a gerçek sayısı için a + 0 = 0 + a = a olduğundan gerçek sayılar kümesinde toplama işleminin etkisiz (birim) elemanı sıfırdır.
Ters Eleman özelliği: a gerçek sayısı için a + (-a) = (-a) + a = 0 olduğundan gerçek sayılar kümesinde her elemanın tersi vardır. Örneğin 5'in toplama işlemine göre tersi -5, -7'nin toplama işlemine göre tersi 7 dir.
Gerçek Sayılarda Çarpma İşleminin Özellikleri
Kapalılık Özelliği: İki gerçek sayının çarpımı daima gerçek sayı olduğu için gerçek sayılar kümesi çarpma işlemine göre kapalıdır.
Değişme Özelliği: a ve b gerçek sayıları için a . b = b . a olduğundan gerçek sayılar kümesinde çarpma işleminin değişme özelliği vardır.
Birleşme Özelliği: a, b ve c birer gerçek sayı olmak üzere (a . b) . c = a . (b . c) olduğundan gerçek sayılar kümesinde çarpma işleminin birleşme özelliği vardır.
Etkisiz Eleman Özelliği (Birim Eleman): a gerçek sayısı için a . 1 = 1 + a = a olduğundan gerçek sayılar kümesinde çarpma işleminin etkisiz (birim) elemanı 1 dir.
Ters Eleman özelliği: a gerçek sayısı için a . (1/a) = (1/a) . a = 1 olduğundan gerçek sayılar kümesinde her elemanın tersi vardır. a sayısının çarpma işlemine göre tersi 1/a dır. Örneğin 5'in çarpma işlemine göre tersi 1/5, -7'nin çarpma işlemine göre tersi -1/7, 2/5 in çarpma işlemine göre tersi de 5/2 dir.
Örnek: 2/3 sayısının toplama işlemine göre tersi a, çarpma işlemine göre tersi b olduğuna göre a + b kaçtır.
Çözüm: 2/3 sayısının toplama işlemine göre tersi -2/3 olduğundan a = -2/3 ve çarpma işlemine göre tersi 3/2 olduğundan b = 3/2 dir. Buna göre, a + b = -2/3 + 3/2 = -4/6 + 9/6 = 5/6
Doğal Sayılar: N = {0, 1, 2, 3, ...} kümesinin elemanlarının her birine doğal sayı denir. En küçük doğal sayı sıfırdır.
Sayma Sayıları: Doğal sayılar kümesinden sıfırın çıkartılması ile elde edilen kümeye sayma sayıları kümesi denir ve N+ ile gösterilir. N+ = {1, 2, 3, 4, ...}
Örnek: x ve y doğal sayılar olmak üzere x + y = 7 olduğuna göre 3x + 2y toplamının alabileceği en küçük değeri bulunuz.
Çözüm: 3x + 2y = x + 2x +2y = x + 2.(x + y) = x + 2.7 =x +14
Sonuç x' e bağlı olduğu için x'e alabileceği en küçük değeri vermemiz gerekir. X doğal sayı olduğundan x= 0 seçersek x + 14= 0 + 14 = 14 olur.
Tam Sayılar: Z = {..., -3, -2, -1, 0, 1, 2, 3, ...} kümesinin elemanlarının her birine tam sayı denir. Tam sayılar kümesi, pozitif tam sayılar, negatif tam sayılar ve sıfırın birleşiminden oluşur.
Z+ = {1, 2, 3, 4, ....} ve Z- = {..., -3, -2, -1} olmak üzere Z = Z+∪ Z- ∪ {0}
n ∈ Z olmak üzere 2n+1 genel ifadesiyle belirtilen tam sayılara tek sayı, 2n genel ifadesiyle belirtilen tam sayılara da çift sayı denir.
Ç = {..., -4, -2, 0, 2, 4, 6, ...} ve T= {..., -5, -3, -1, 1, 3, 5, 7, ...}
Her doğal sayı aynı zamanda tam sayı olduğu için doğal sayılar kümesi tam sayılar kümesinin alt kümesidir. (N ⊂ Z )
Örnek: a ile b birer tam sayı ve a + b = 14 ise a.b ifadesinin alabileceği en büyük değer kaçtır.
Çözüm: Toplamları sabit olan iki gerçek sayının çarpımlarının en büyük olabilmesi için sayıların bir birine yakın seçilmesi gerekir. Toplamları 14 olan birbirine yakın iki sayı 7 ve 7 dir.
a.b en fazla 7.7'den 49 olur.
Örnek: a ile b birer negatif tam sayıdır. a.b = 7 ve b - c = -3 olduğuna göre, a + b + c toplamını bulunuz.
Çözüm: a.b = 7 olduğuna göre (a = -7 ve b = -1) veya ( a = -1 ve b = -7) dir.
b = -1 ve b - c = -3 için -1 - c = -3, -c = -2 ve c =2 olur. 2 negatif tam sayı olmadığı için c 2 olamaz.
b = -7 ve b - c = -3 için -7 - c = -3, - c = 4 ve c = -4 tür. Buna göre a + b + c = (-1) + (-7) + (-4) = -12 olur.
Rasyonel Sayılar: a, b tam sayı ve b sıfırdan farklı olmak üzere a/b ifadesine rasyonel sayı ya da kesir denir. a ya kesrin payı, b ye de paydası denir. Rasyonel sayılar kümesi Q sembolü ile gösterilir. Rasyonel sayılarda payda sıfır olursa sayı tanımsız olur.
a / b kesrinin pay ve paydasını sıfırdan farklı bir tam sayı ile çarpmaya genişletme, pay ve paydasını sıfırdan farklı bir tam sayı ile bölmeye sadeleştirme denir.

Rasyonel sayılarda toplama ve çıkarma işleminin yapılabilmesi için paydalarının eşit olması gerekir, Eşit değilse genişletme işlemi ile paydalar eşitlenir.


Rasyonel Sayılarda Sıralama:
* Paydalar eşit ise payı büyük olan daha büyüktür.
* Paylar eşit ise paydası küçük olan daha büyüktür.
* Pay ile payda arasındaki farklar eşit ise basit kesirlerde paydası büyük olan büyüktür, bileşik kesirlerde paydası büyük olan küçüktür.
İrrasyonel Sayılar: Rasyonel olmayan gerçek sayılara irrasyonel sayılar denir ve Q' ile gösterilir. İrrasyonel sayılar a/b şeklinde yazılamazlar.
Gerçek (Reel) Sayılar: Rasyonel sayılar kümesi ile irrasyonel sayılar kümesinin birleşiminden oluşan kümeye gerçek sayılar kümesi denir ve R ile gösterilir. R = Q ∪ Q'
- Her sayma sayısı bir doğal sayıdır.
- Her doğal sayı bir tam sayıdır.
- Her tam sayı bir rasyonel sayıdır.
- Her rasyonel sayı bir gerçek sayıdır.
- Her irrasyonel sayı bir gerçek sayıdır.
Gerçek Sayılarda Toplama İşleminin Özellikleri
Kapalılık Özelliği: İki gerçek sayının toplamı daima gerçek sayı olduğu için gerçek sayılar kümesi toplama işlemine göre kapalıdır.
Değişme Özelliği: a ve b gerçek sayıları için a + b = b + a olduğundan gerçek sayılar kümesinde toplama işleminin değişme özelliği vardır.
Birleşme Özelliği: a, b ve c birer gerçek sayı olmak üzere (a + b) + c = a + (b + c) olduğundan gerçek sayılar kümesinde toplama işleminin birleşme özelliği vardır.
Etkisiz Eleman Özelliği (Birim Eleman): a gerçek sayısı için a + 0 = 0 + a = a olduğundan gerçek sayılar kümesinde toplama işleminin etkisiz (birim) elemanı sıfırdır.
Ters Eleman özelliği: a gerçek sayısı için a + (-a) = (-a) + a = 0 olduğundan gerçek sayılar kümesinde her elemanın tersi vardır. Örneğin 5'in toplama işlemine göre tersi -5, -7'nin toplama işlemine göre tersi 7 dir.
Gerçek Sayılarda Çarpma İşleminin Özellikleri
Kapalılık Özelliği: İki gerçek sayının çarpımı daima gerçek sayı olduğu için gerçek sayılar kümesi çarpma işlemine göre kapalıdır.
Değişme Özelliği: a ve b gerçek sayıları için a . b = b . a olduğundan gerçek sayılar kümesinde çarpma işleminin değişme özelliği vardır.
Birleşme Özelliği: a, b ve c birer gerçek sayı olmak üzere (a . b) . c = a . (b . c) olduğundan gerçek sayılar kümesinde çarpma işleminin birleşme özelliği vardır.
Etkisiz Eleman Özelliği (Birim Eleman): a gerçek sayısı için a . 1 = 1 + a = a olduğundan gerçek sayılar kümesinde çarpma işleminin etkisiz (birim) elemanı 1 dir.
Ters Eleman özelliği: a gerçek sayısı için a . (1/a) = (1/a) . a = 1 olduğundan gerçek sayılar kümesinde her elemanın tersi vardır. a sayısının çarpma işlemine göre tersi 1/a dır. Örneğin 5'in çarpma işlemine göre tersi 1/5, -7'nin çarpma işlemine göre tersi -1/7, 2/5 in çarpma işlemine göre tersi de 5/2 dir.
Örnek: 2/3 sayısının toplama işlemine göre tersi a, çarpma işlemine göre tersi b olduğuna göre a + b kaçtır.
Çözüm: 2/3 sayısının toplama işlemine göre tersi -2/3 olduğundan a = -2/3 ve çarpma işlemine göre tersi 3/2 olduğundan b = 3/2 dir. Buna göre, a + b = -2/3 + 3/2 = -4/6 + 9/6 = 5/6