Gerçek Sayılar Çözümlü Sorular

Gerçek Sayılar Test 1 Çöz

Çözümlü Örnek Test Soruları: Gerçek Sayılar

1. Bir sayının karesi kendisine eşitse, bu sayı aşağıdakilerden hangisi olabilir?
A) 0 veya 1
B) 1 veya -1
C) 0 veya -1
D) 1 veya 2

Çözüm:
Bir sayının karesi kendisine eşitse, x² = x denklemi sağlanmalıdır. Denklem x² – x = 0 olarak yazılıp çarpanlara ayrılır:
x(x – 1) = 0
Buradan x = 0 veya x = 1 bulunur.
Cevap: A

2. Bir gerçek sayının küpü kendisine eşittir. Bu sayı aşağıdakilerden hangisi olamaz?
A) 1
B) 0
C) -1
D) 2

Çözüm:
Verilen koşul için x³ = x denklemi sağlanmalıdır. Denklem şu şekilde yazılır:
x³ – x = 0 → x(x² – 1) = 0 → x(x – 1)(x + 1) = 0
Buradan x = 0, x = 1, x = -1 bulunur. Ancak 2 sayısı bu denklemi sağlamaz.
Cevap: D

3. Gerçek sayılar kümesinde tanımlı olmayan ifade aşağıdakilerden hangisidir?
A) √4
B) 5 / 0
C) -√9
D) 0²

Çözüm:
Gerçek sayılar kümesinde bir sayının sıfıra bölümü tanımsızdır. Diğer ifadeler geçerlidir:

• √4 = 2,
• -√9 = -3,
• 0² = 0
  Ancak 5 / 0 tanımsızdır.
  Cevap: B

4. İki ardışık gerçek sayının çarpımı 72’dir. Küçük sayı aşağıdakilerden hangisidir?
A) 8
B) 9
C) 7
D) 6

Çözüm:
Ardışık iki sayıyı x ve x + 1 olarak tanımlayalım:
x(x + 1) = 72
Denklemi çözelim:
x² + x – 72 = 0
Çarpanlarına ayırarak:
(x – 8)(x + 9) = 0
Buradan x = 8 veya x = -9 bulunur. Küçük sayı -9’dur.
Cevap: B

5. Aşağıdaki ifadelerden hangisi bir rasyonel sayı değildir?
A) 5 / 2
B) √16
C) 3.14159265…
D) -7 / 3

Çözüm:

• 5 / 2 ve -7 / 3 rasyonel sayıdır çünkü iki tam sayının oranı şeklindedir.
• √16 = 4 bir tam sayıdır ve dolayısıyla rasyoneldir.
• π ≈ 3.14159265… irrasyonel bir sayıdır.
  Cevap: C

• ---

Soru: a , b ve c sıfırdan farklı birer doğal sayı olmak üzere,
a+b+c= 15
eşitliğini sağlayan a, b ve c değerleri için a. b . c çarpımının alabileceği en büyük ve en küçük değerlerin toplamı kaçtır?
Çözüm: a.b. c çarpımının en büyük olması için a, b ve c doğal sayıları mümkün olduğu kadar birbirine yakın seçilmelidir. En küçük olması için a, b ve c doğal sayılarından birine mümkün olduğunca büyük değer verilir.
a+b+ç=15 ve a+b+ç=15
a.b.c çarpımının değeri en az 13 ve en çok 125 tir. Buna göre, cevap 13 +125 = 138 olur.

Soru: a, b ve c pozitif tam sayılardır.
a.b . c = 28
olduğuna göre a + b + c toplamının alabileceği en büyük ve en küçük değerlerin toplamı kaçtır?
Çözüm: a + b + c toplamının en büyük olması için a , b ve c doğal sayılarından biri mümkün olduğunca büyük seçilmelidir. En küçük olması için a, b ve c doğal sayılarına mümkün olduğunca birbirine yakın değerler verilir.
a.b.ç=28 ve a.b.ç=28
1+1+28=30 2+2+7=11
a+ b + ctoplamının değeri en çok 30 ve en az 11 dir. Buna göre, cevap 30 + 11 = 41 olur.

Soru: a, b ve c pozitif tam sayılardır.
a.b = 24
b.c = 30
olduğuna göre, a + b + c toplamı kaç farklı değer alır?
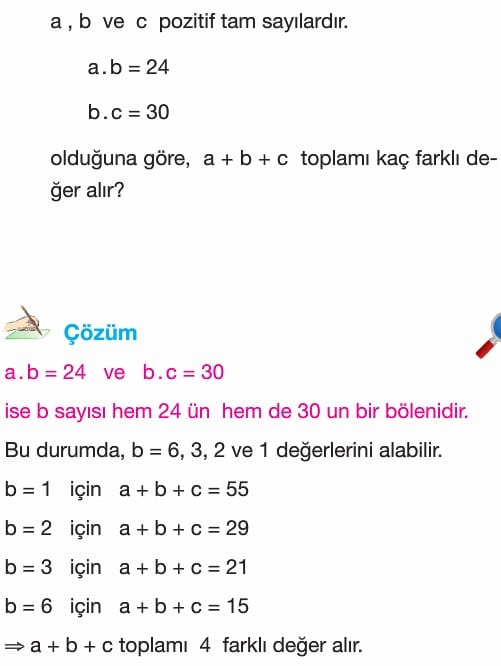
Çözüm: a . b = 24 ve b . c = 30
ise b sayısı hem 24 ün hem de 30 un bir bölenidir. Bu durumda, b = 6, 3, 2 ve 1 değerlerini alabilir.
b=1 için a+b+c=55
b=2 için a+b+c=29
b=3 için a+b+c=21
b=6 için a+b+c=15
a + b + c toplamı 4 farklı değer alır.

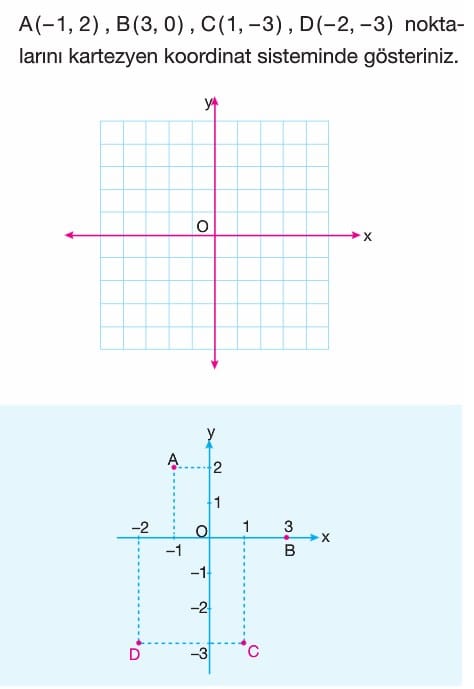
Gerçek sayılar kümesinin (R) geometrik temsili sayı doğrusudur. Sayı doğrusu üzerinde boş nokta yoktur. R x R nin geometrik temsili kartezyen koordinat sistemidir. Kartezyen koordinat sistemi birbirine dik iki sayı doğrusunun sıfır noktasında kesişmesi ile elde edilmiştir. Yatay eksene x ekseni, düşey eksene y ekseni denir.

Soru: Aşağıdakilerden hangisi yanlıştır?
A) Her doğal sayı bir tam sayıdır.
B) Sıfır bir tam sayıdır.
C) Her tam sayı bir doğal sayıdır.
D) En küçük doğal sayı sıfırdır.
E) Her pozitif doğal sayı bir sayma sayısıdır.
Cevap: C) Negatif tam sayılar doğal sayı değildir.

Soru: Aşağıdakilerden hangisi yanlıştır?
A) Her sayma sayısı bir doğal sayıdır.
B) Her tam sayı bir sayma sayısıdır.
C) Her tam sayı bir rasyonel sayıdır.
D) Her rasyonel sayı bir gerçek(reel) sayıdır.
E) Her irrasyonel sayı bir gerçek(reeI) sayıdır.
Cevap: B) Negatif tam sayılar ve {0} sayma sayısı değildir.