Fonksiyon Grafiğinin Eksenleri Kestiği Noktalar

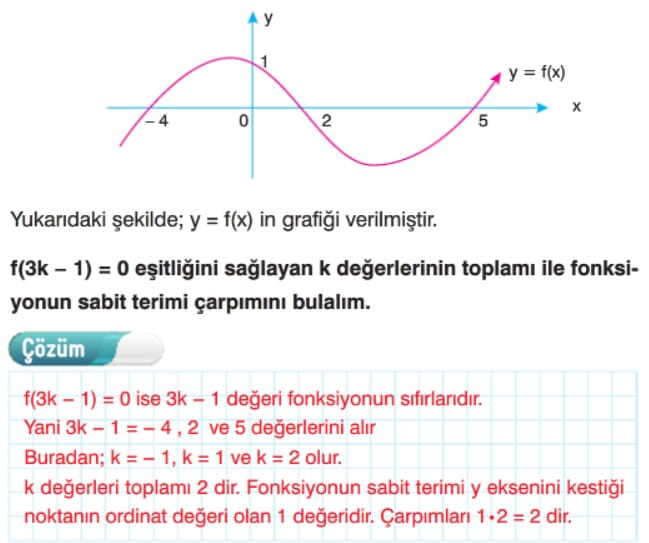
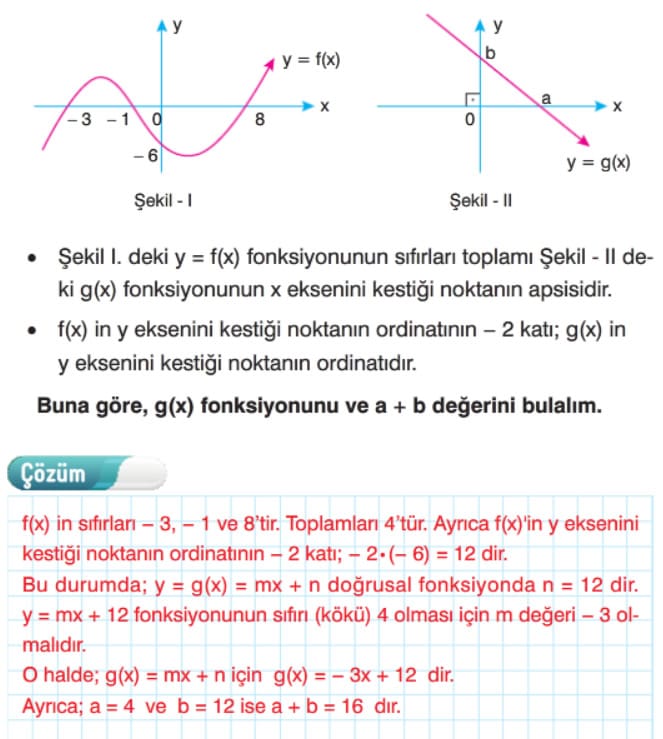
Fonksiyon Grafiğinin Eksenleri Kestiği Noktalar Çözümlü Sorular

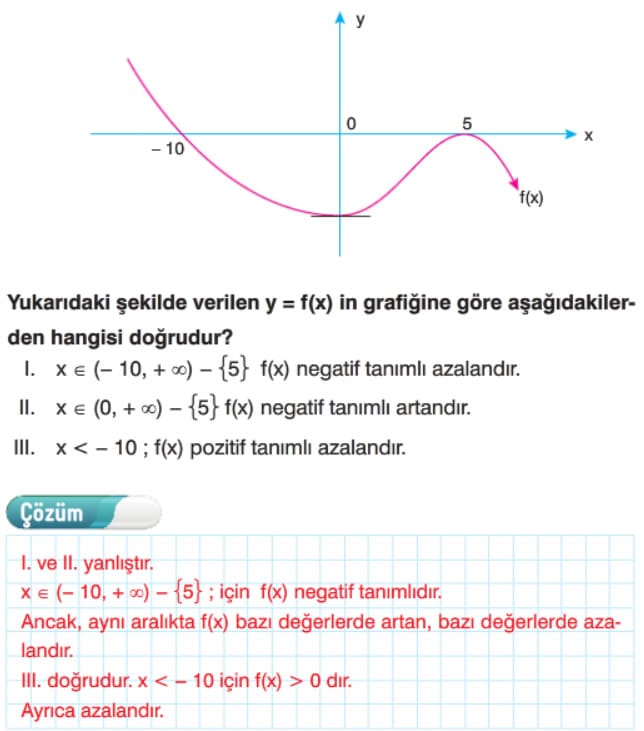
Fonksiyonun Pozitif – Negatif Olduğu Aralıklar

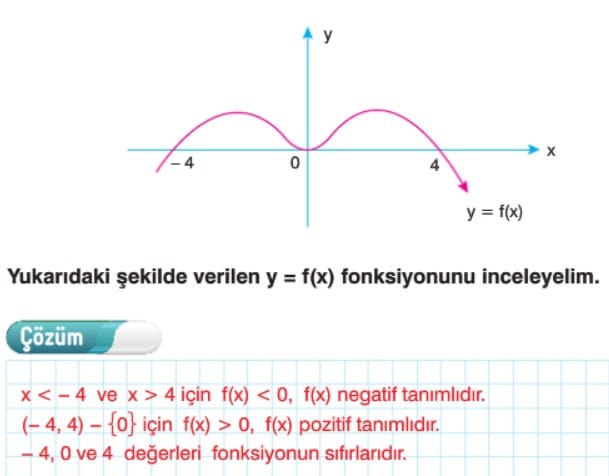
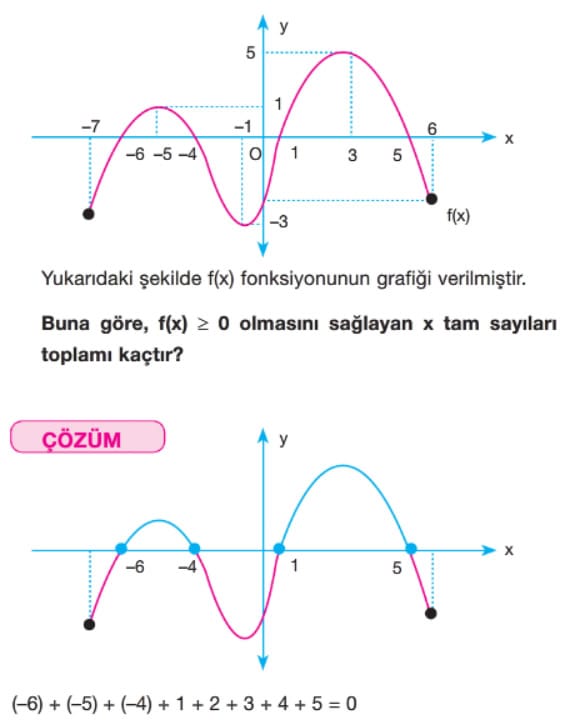
Fonksiyonun Pozitif – Negatif Olduğu Aralıklar Çözümlü Sorular

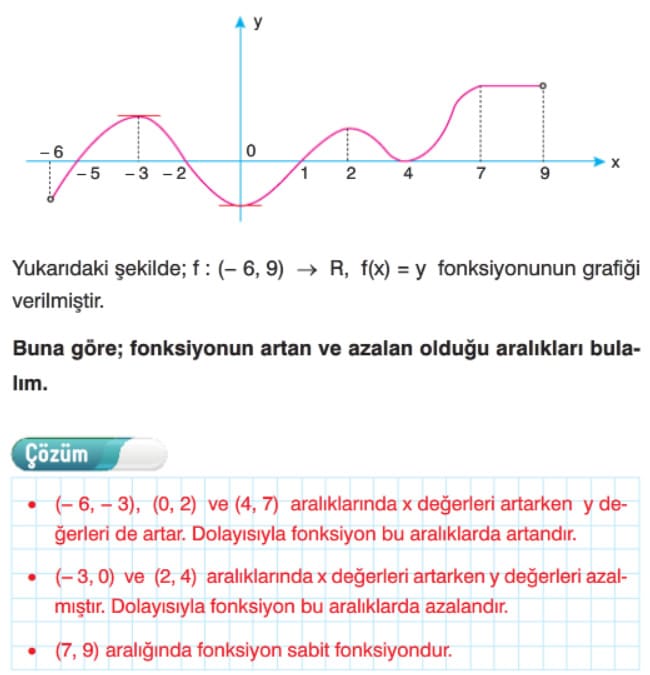
Fonksiyonun Artan ve Azalan Olduğu Aralıklar

Fonksiyonun Artan ve Azalan Olduğu Aralıklar Çözümlü Sorular

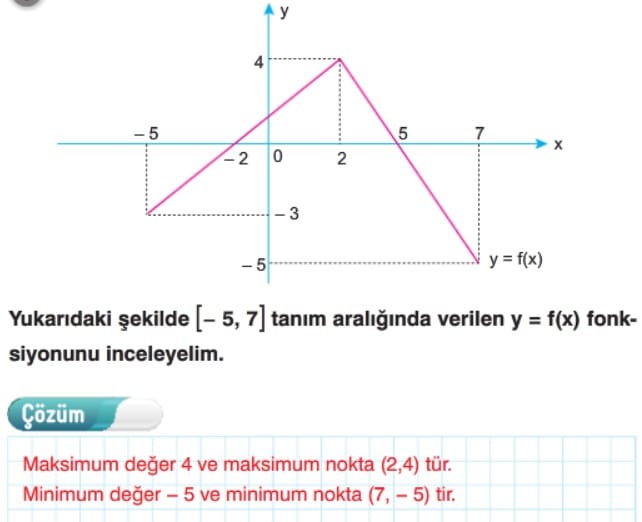
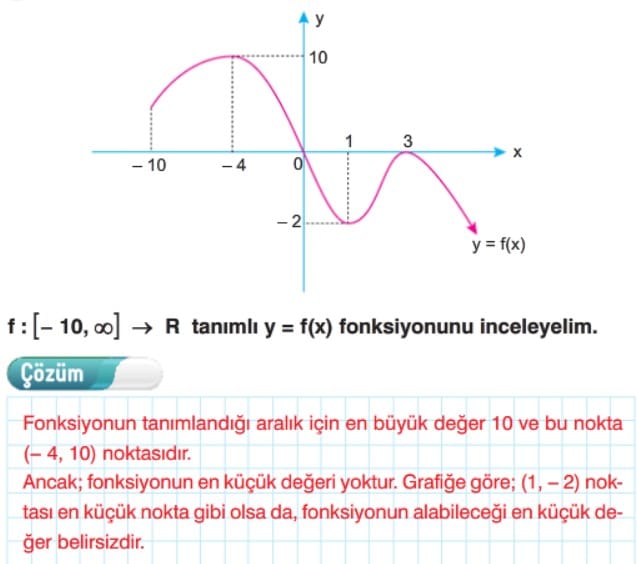
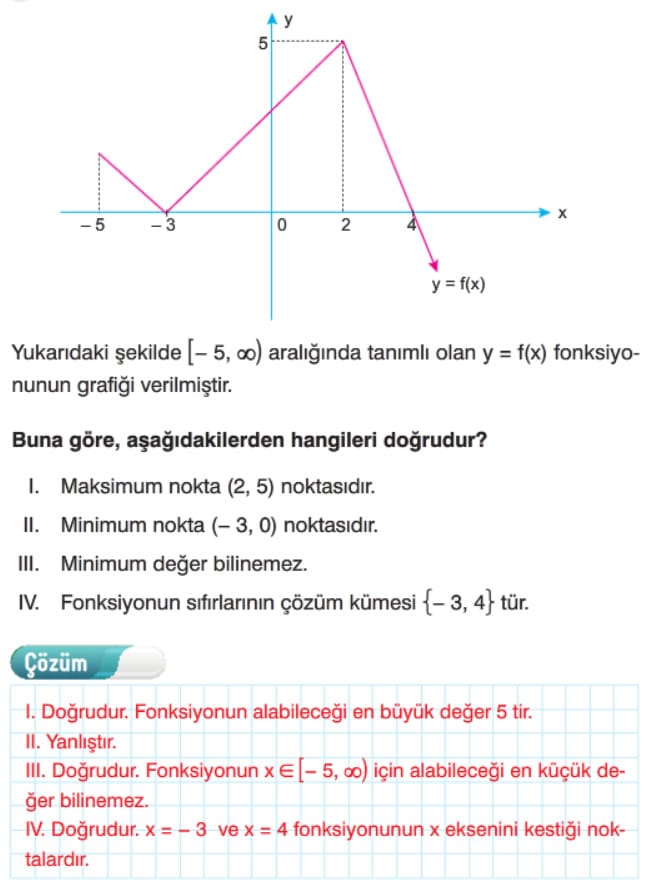
Fonksiyonun Maksimum ve Minimum Noktaları ve Değerleri

Analitik düzlemde, fonksiyon grafiğinin görüntü kümesinde aldığı en büyük değere fonksiyonun maksimum değeri, bu değeri aldığı nokta ise maksimum noktaya denir. Aynı şekilde, fonksiyonun grafiğinin görüntü kümesinde aldığı en küçük değere fonksiyonun minimum değeri, bu değeri aldığı noktaya ise minimum nokta denir.

Fonksiyonun Maksimum ve Minimum Noktaları ve Değerleri Çözümlü Sorular

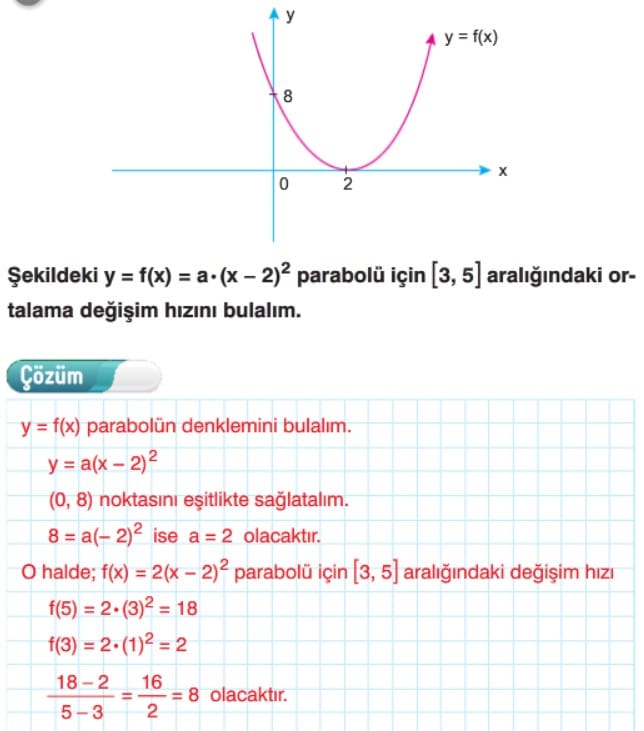
Ortalama Değişim Hızı

Ortalama Değişim Hızı Çözümlü Sorular

Çözümlü Örnek Test Soruları: Fonksiyonlarla İlgili Uygulamalar

Soru 1:

f(x) = 3x + 5 fonksiyonunda f(2) kaçtır?
A) 9
B) 10
C) 11
D) 12

Cevap: C
Çözüm: Fonksiyonda f(x) = 3x + 5 olduğu verilmiştir. f(2) hesaplanır:
f(2) = 3 * 2 + 5 = 6 + 5 = 11.

Soru 2:

g(x) = x * x – 4 ve h(x) = x + 2 fonksiyonları veriliyor. (g o h)(x) fonksiyonu nedir?
A) x * x + 4x – 4
B) x * x + 4x + 4
C) x * x – 4
D) x * x – 8x – 4

Cevap: A
Çözüm: Bileşke fonksiyon g(h(x)) olarak hesaplanır:
h(x) = x + 2, bunu g(x) = x * x – 4’te yerine koyarsak:
g(h(x)) = (x + 2) * (x + 2) – 4 = x * x + 4x + 4 – 4 = x * x + 4x – 4.

Soru 3:

Bir fonksiyon f(x) = 2x + 3 olarak verilmiştir. f ters(x), yani fonksiyonun tersini bulunuz.
A) f ters(x) = x – 3 / 2
B) f ters(x) = (x – 3) / 2
C) f ters(x) = (x + 3) / 2
D) f ters(x) = 2x – 3

Cevap: B
Çözüm: Fonksiyonun tersini bulmak için y = 2x + 3 olarak yazılır ve x’i yalnız bırakırız:
y = 2x + 3 → x = (y – 3) / 2.
Tersi: f ters(x) = (x – 3) / 2.

Soru 4:

f(x) = 2x – 1 ve g(x) = x + 3 fonksiyonları veriliyor. (f o g)(2) nedir?
A) 9
B) 10
C) 11
D) 12

Cevap: A
Çözüm: Bileşke fonksiyon f(g(2)) olarak hesaplanır.
Önce g(2) hesaplanır:
g(2) = 2 + 3 = 5.
Sonra bu değer f(x) = 2x – 1’e yerleştirilir:
f(5) = 2 * 5 – 1 = 10 – 1 = 9.

Soru 5:

Bir fonksiyon f(x) = x * x – 2x + 1 olarak verilmiştir. Fonksiyon sabit bir değer alıyorsa, bu hangi x değeri içindir?
A) 0
B) 1
C) 2
D) 3

Cevap: B
Çözüm: Fonksiyon f(x) = x * x – 2x + 1’dir.
Bu ifadeyi çarpanlarına ayırırsak: f(x) = (x – 1) * (x – 1).
Fonksiyon sabit bir değer aldığında, x = 1 olur ve f(x) = 0 değerini verir.

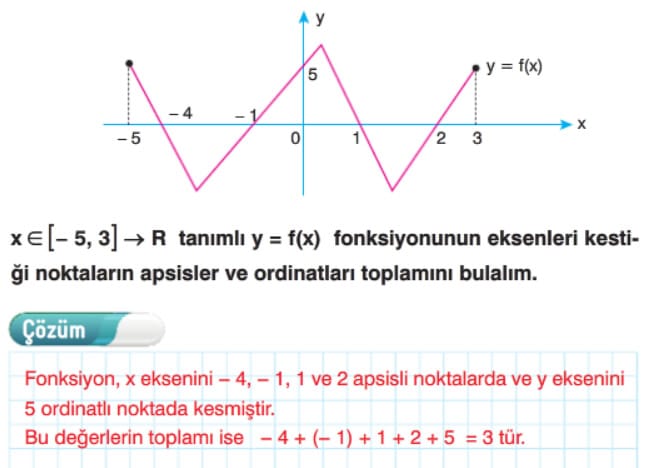
FONKSİYONLARIN GRAFİĞİNİN EKSENLERİ KESTİĞİ NOKTALAR

• Bir fonksiyonun grafiğinin x eksenini kestiği noktalarda y = 0 dır.
• Fonksiyonun y eksenini kestiği noktalarda ise x = 0 dır.

Bilgi: Bir fonksiyon, grafiğinin x ekseni üzerinde kalan aralıklarda pozitif değerlidir. Fonksiyon, grafiğinin x ekseni altında kaldığı aralıklarda ise negatif değerlidir.

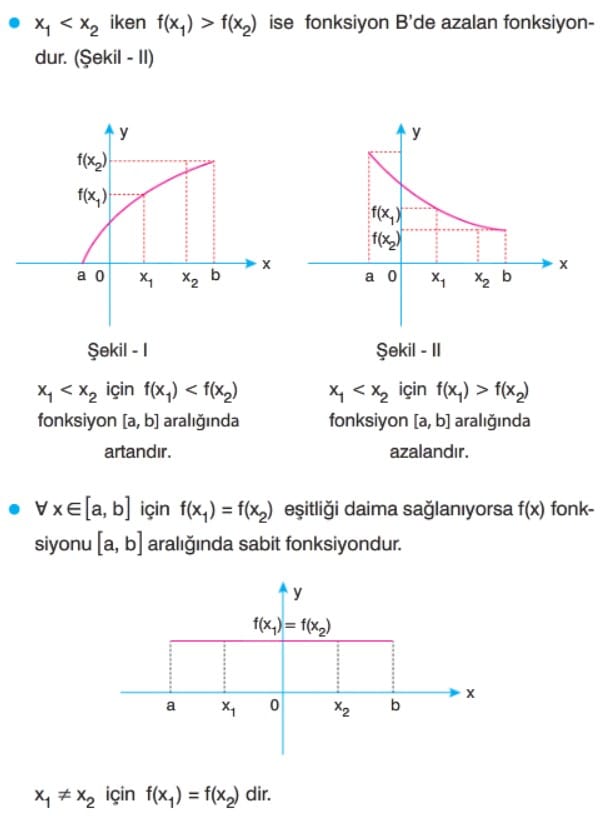
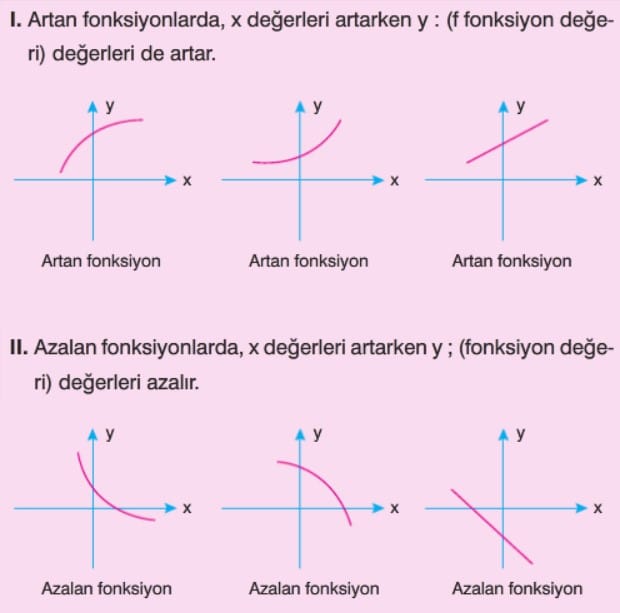
ARTAN-AZALAN FONKSİYON

• Bir aralıktaki her x₁ < x₂ için f(x₁) < f(x₂) sağlanıyorsa f fonksiyonu 0 aralıkta artandır.
• Bir aralıkta her x₁ < x₂ için f(x₁) > f(x₂) sağlanıyorsa f fonksiyonu o aralıkta azalandır.
• Bir aralıkta her x₁ < x₂ için f(x₁) = f(x₂) sağlanıyorsa f fonksiyonu o aralıkta sabittir.

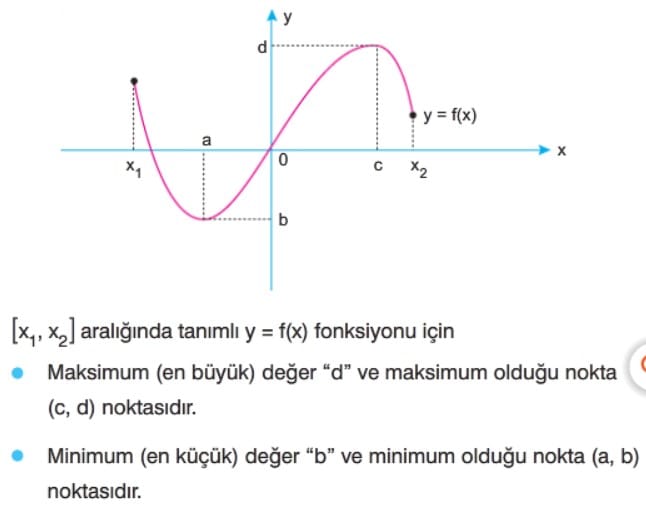
BİR FONKSİYONUN BİR ARALIKTA ALDIĞI MAKSİMUM-MİNİMUM DEĞERLER

• Bir [a, b] aralığında x₀ ∈ [a, b] olmak üzere; ∀ x₁ ∈ [a, b] için f(x₀) ≤ f(x₁) ise f(x₀) değerine fonksiyonun [a, b] aralığındaki minimum değeri denir. Bir aralıktaki minimum değeri için yerel minimum ifadesi de kullanılır.
• Bir [a, b] aralığında x₀ ∈ [a, b] olmak üzere ∀ x₁ ∈ [a, b] için f(x₀) ≥ f(x₁) ise f(x₀) değerine fonksiyonun [a, b] aralığındaki maksimum değeri denir. Bir aralıktaki maksimum değeri için yerel maksimum ifadesi de kullanılır.

Fonksiyonun Bir Aralıkta Ortalama Değişim Hızı

Bir fonksiyonun [a, b] aralığındaki ortalama değişim hızı

f(b) – f(a)b-a

formülüyle hesaplanır. Ortalama değişim hızına, fonksiyonu a ve b noktalarında kesen doğrunun eğimi de denir.

Bilgi: f bir doğrusal fonksiyonsa doğrunun eğimi ortalama değişim hızına eşittir. Yani f(x) = ax + b ise ortalama değişim hızı a sayısına eşittir.