Fonksiyonların Dönüşümleri 11. Sınıf
Fonksiyonların Dönüşümleri online test çözmek için tıklayın.
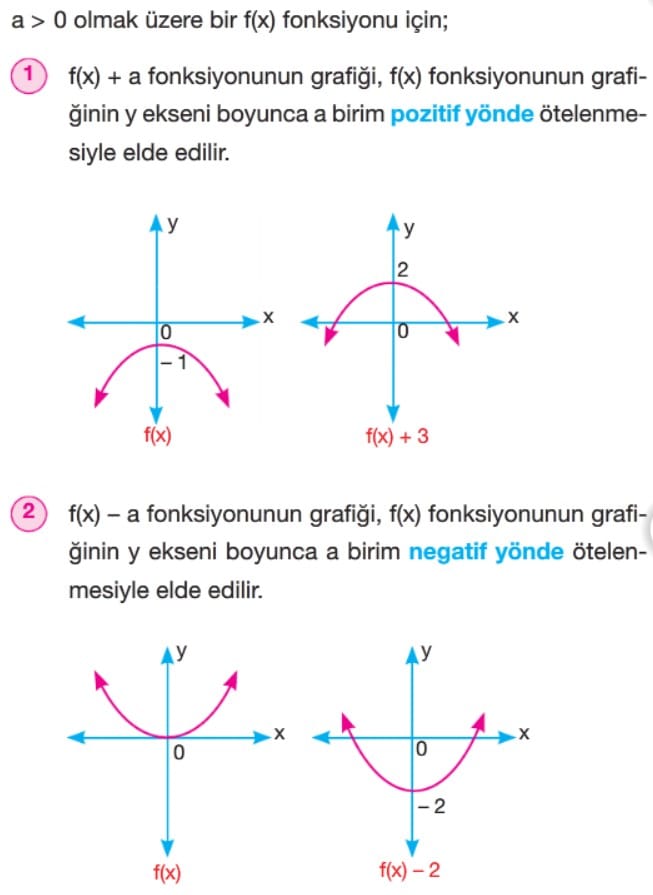
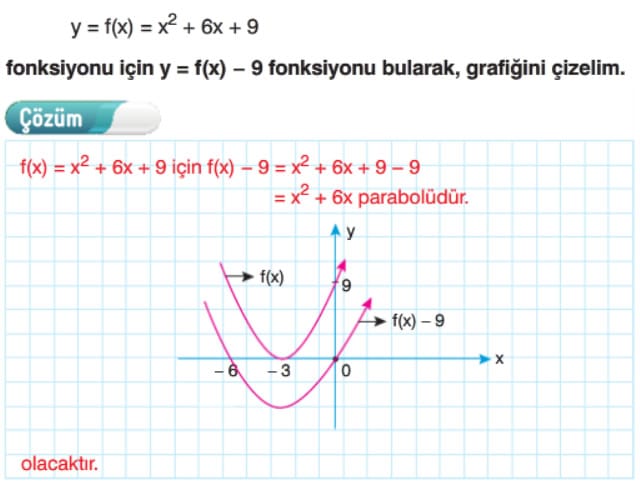
Örnek:
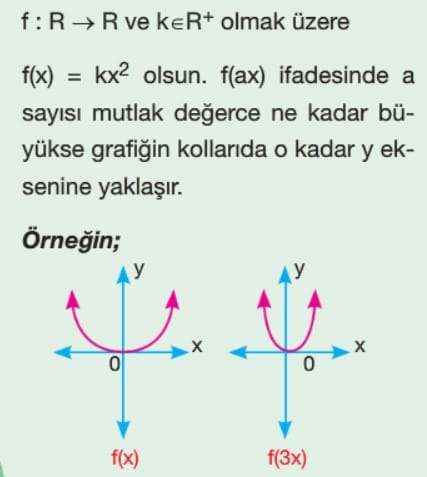
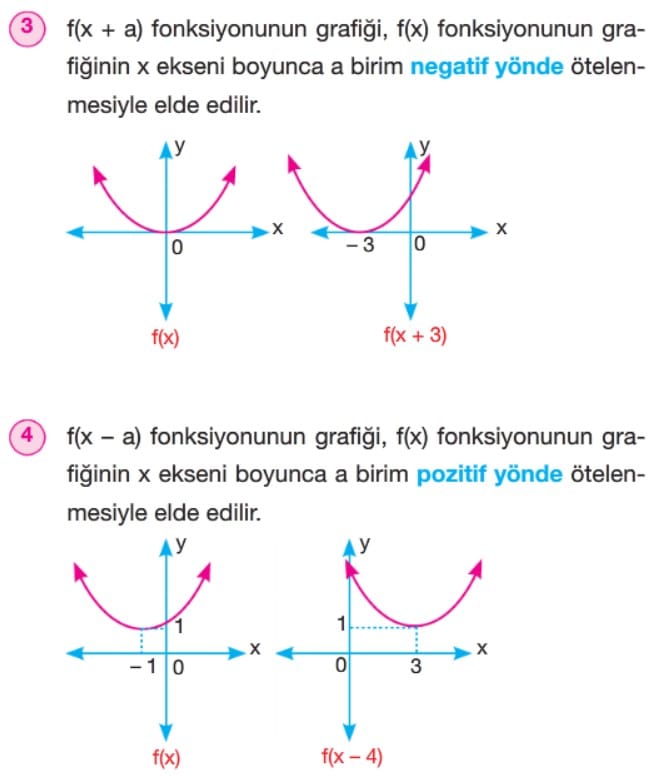
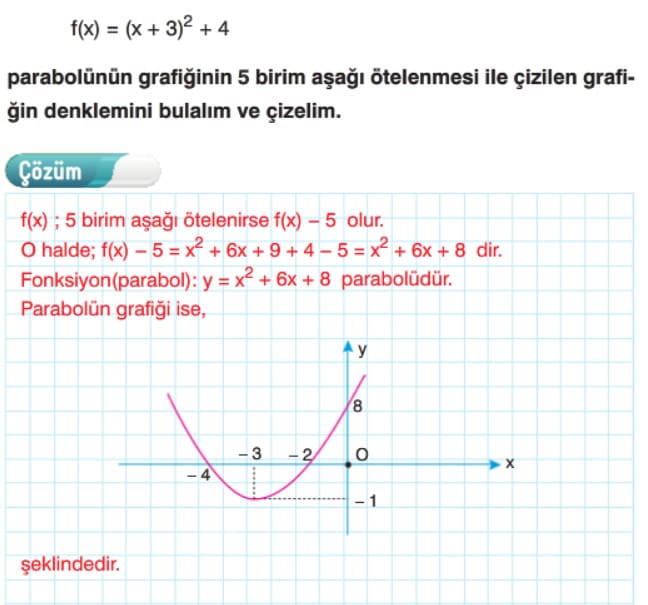
Örnek:
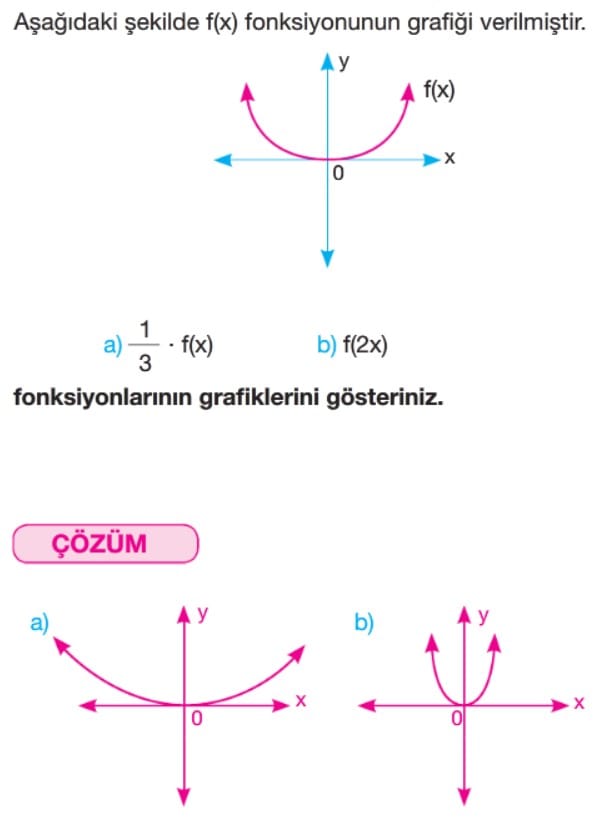
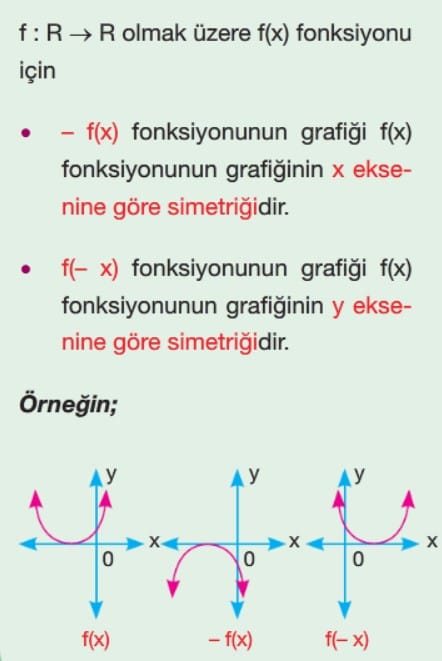
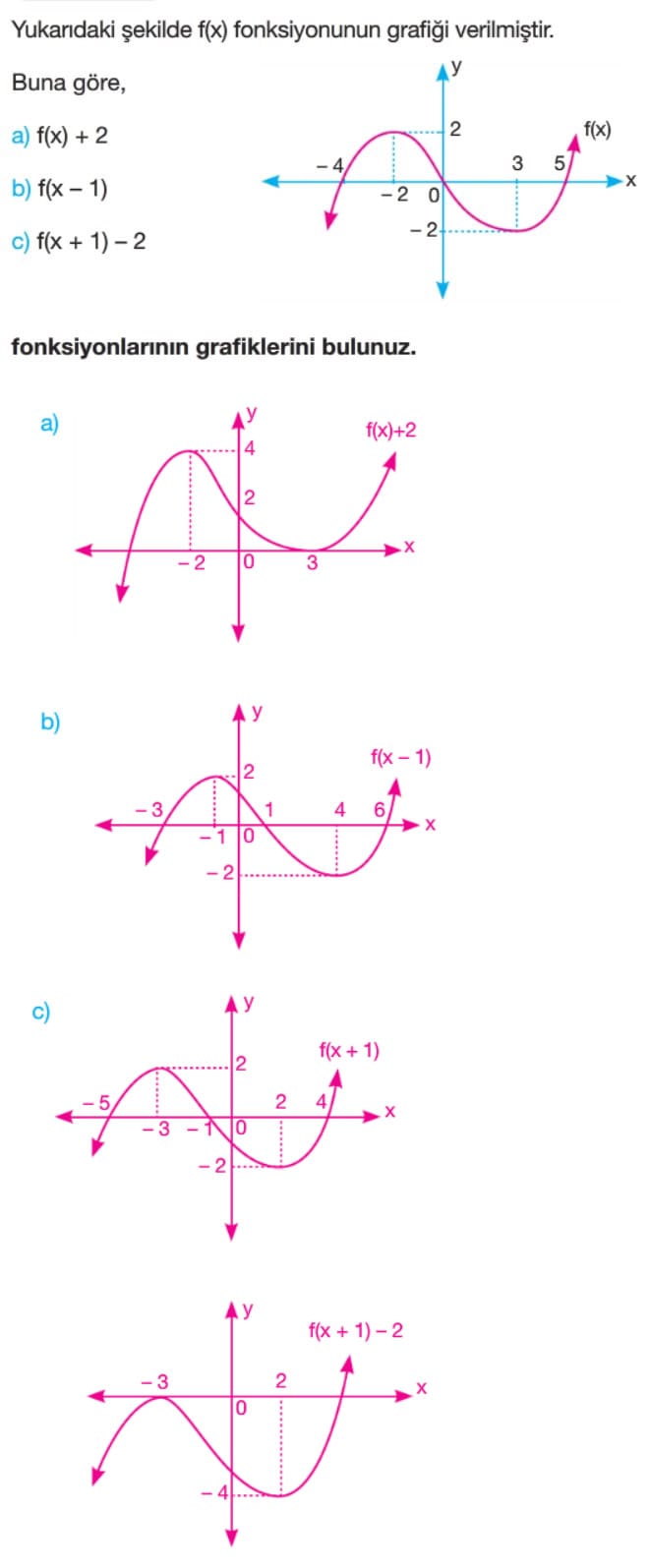
Örnek:
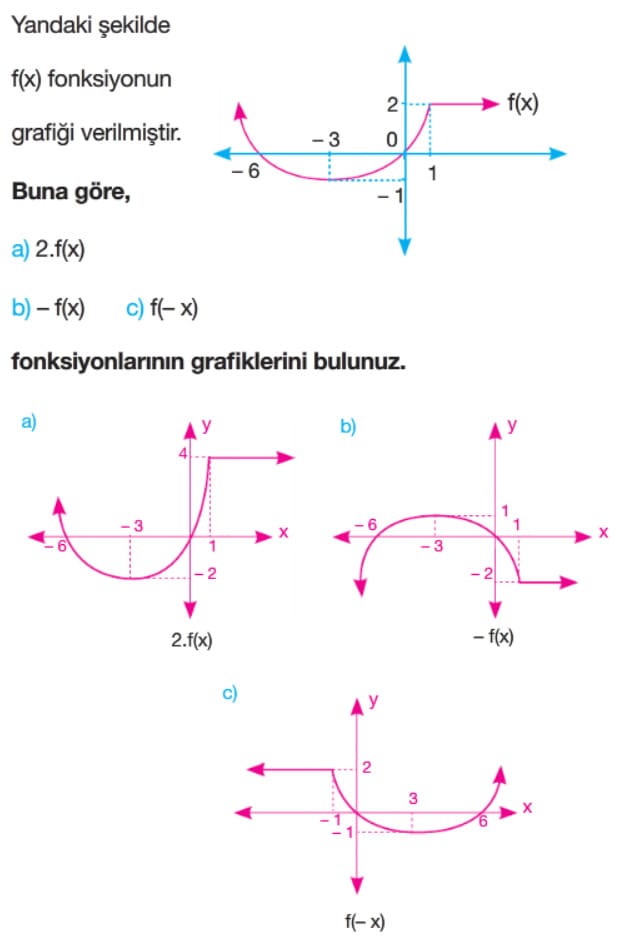

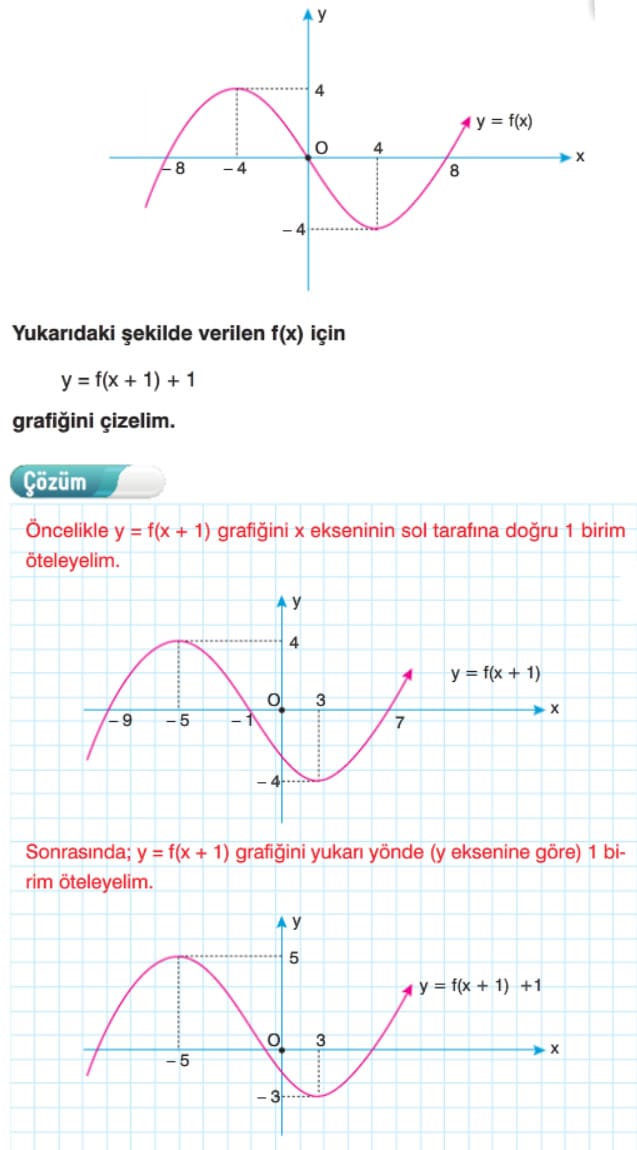
Örnek:

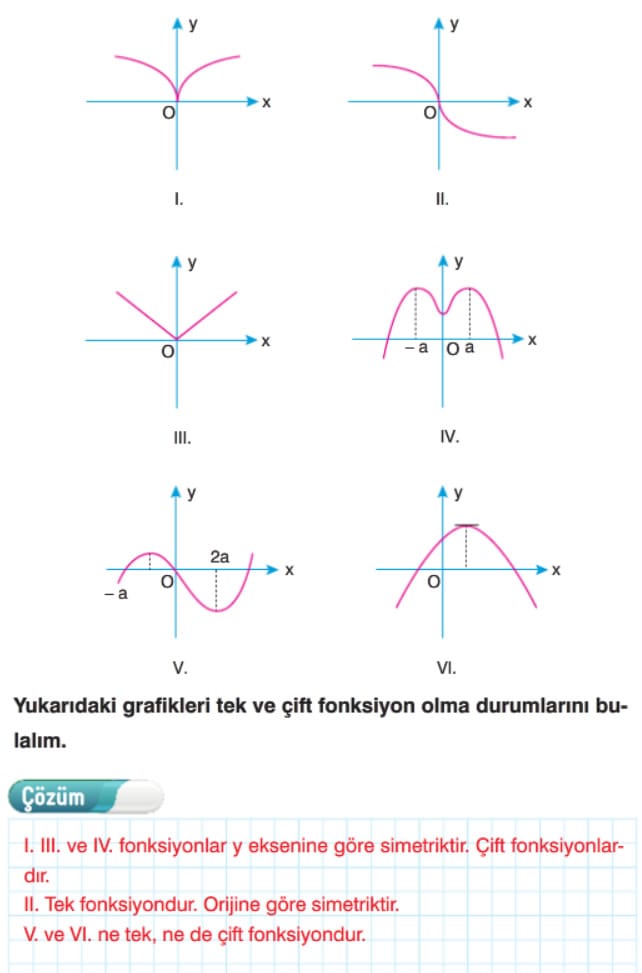
Tek ve Çift Fonksiyonlar

Örnek:

Örnek:
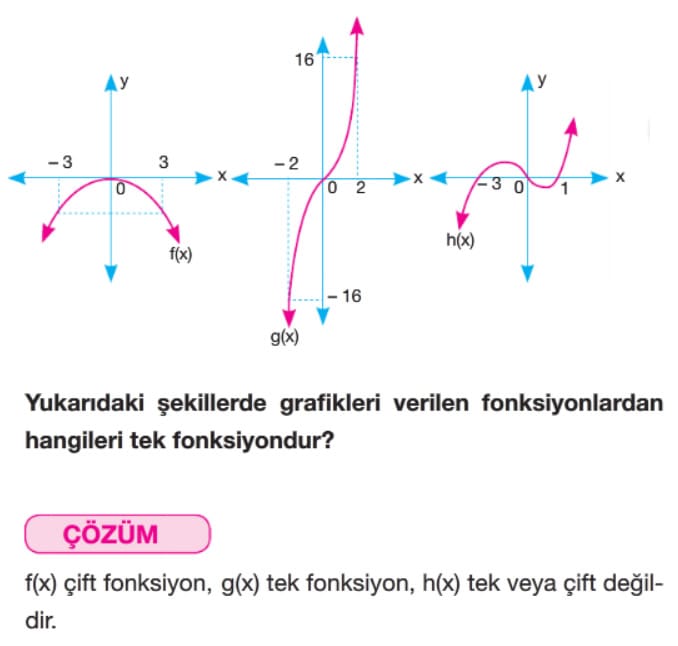
Örnek:

Fonksiyonların Dönüşümleri Çözümlü Sorular
Çözümlü Örnek Sorular
Soru 1:
Verilen fonksiyon f(x) = x² – 2x + 3, 4 birim yukarı kaydırıldığında yeni fonksiyon aşağıdakilerden hangisi olur?
A) f(x) = x² – 2x – 1
B) f(x) = x² – 2x + 7
C) f(x) = x² – 2x – 3
D) f(x) = x² – 2x + 3
Çözüm:
Fonksiyonu yukarı kaydırmak, sabit bir sayı eklemekle yapılır. 4 birim yukarı kaydırıldığında:
Yeni fonksiyon f(x) = x² – 2x + 3 + 4 = x² – 2x + 7 olacaktır.
Cevap: B)
Soru 2:
f(x) = x² fonksiyonu 2 birim sola kaydırılırsa, elde edilen fonksiyon aşağıdakilerden hangisidir?
A) f(x) = (x – 2)²
B) f(x) = (x + 2)²
C) f(x) = (x – 2)² + 2
D) f(x) = x² – 2
Çözüm:
Bir fonksiyon sola kaydırıldığında x yerine (x + 2) yazılır. Bu durumda yeni fonksiyon:
f(x) = (x + 2)² olacaktır.
Cevap: B)
Soru 3:
Verilen f(x) = -3x² fonksiyonunun Y eksenine göre yansıması aşağıdakilerden hangisidir?
A) f(x) = -3(-x)²
B) f(x) = -3x²
C) f(x) = 3x²
D) f(x) = 3(-x)²
Çözüm:
Bir fonksiyon Y eksenine göre yansıtıldığında x yerine -x yazılır. Bu durumda:
f(x) = -3(-x)² = -3x² olacaktır.
Cevap: B)
Soru 4:
f(x) = 2x fonksiyonu 3 birim sağa kaydırıldığında elde edilen fonksiyon aşağıdakilerden hangisidir?
A) f(x) = 2(x – 3)
B) f(x) = 2x + 3
C) f(x) = 2(x + 3)
D) f(x) = 2(x – 3)²
Çözüm:
Bir fonksiyonu sağa kaydırmak için x yerine (x – 3) yazılır. Bu durumda yeni fonksiyon:
f(x) = 2(x – 3) olacaktır.
Cevap: A)
Soru 5:
f(x) = x² – 4x + 1 fonksiyonunu 5 birim aşağı kaydırırsak elde edilen fonksiyon aşağıdakilerden hangisidir?
A) f(x) = x² – 4x + 6
B) f(x) = x² – 4x – 4
C) f(x) = x² – 4x – 3
D) f(x) = x² – 4x + 1
Çözüm:
Fonksiyonu aşağı kaydırmak, sabit bir sayı çıkarmakla yapılır. 5 birim aşağı kaydırıldığında:
Yeni fonksiyon f(x) = x² – 4x + 1 – 5 = x² – 4x – 4 olacaktır.
Cevap: B)
Soru 6:
f(x) = 4x fonksiyonu dikey olarak 3 katına çıkarıldığında yeni fonksiyon aşağıdakilerden hangisi olur?
A) f(x) = 4x + 3
B) f(x) = 12x
C) f(x) = 4x³
D) f(x) = 4(3x)
Çözüm:
Dikey olarak ölçeklendirme, fonksiyonun tamamını bir katsayı ile çarpmaktır. 3 katına çıkarıldığında:
Yeni fonksiyon f(x) = 3(4x) = 12x olacaktır.
Cevap: B)
Soru 7:
f(x) = 3x² – 2 fonksiyonunun X eksenine göre yansıması nedir?
A) f(x) = -3x² + 2
B) f(x) = 3x² + 2
C) f(x) = -3x² – 2
D) f(x) = 3(-x)² – 2
Çözüm:
X eksenine göre yansıma yapılırken, fonksiyonun tamamının işareti değiştirilir. Bu durumda:
Yeni fonksiyon f(x) = -(3x² – 2) = -3x² + 2 olacaktır.
Cevap: A)
Soru 8:
f(x) = x² + 5x + 3 fonksiyonunun ters fonksiyonu aşağıdakilerden hangisidir?
A) f^-1(x) = (x – 3) / 5
B) f^-1(x) = (x + 3)²
C) f^-1(x) = (x – 3) / x
D) f^-1(x) bulunamaz
Çözüm:
Bu tür ikinci dereceden fonksiyonlar ters fonksiyonla ifade edilemez.
Cevap: D)
Dikkat:
1. Grafiği verilen bir fonksiyon çift fonksiyon ise f (–x) = f (x) olduğundan y = f (x) ile y = f (–x) fonksiyonlarının grafikleri aynıdır.
2. Grafiği verilen bir fonksiyon tek fonksiyon ise f (–x) = –f(x) olduğundan y = f (–x) ile y = –f (x) fonksiyonlarının grafikleri aynıdır.
Öğrenelim: Günlük yaşantıda bazı nesneleri gruplandırırız. Örneğin hayvanları karada, denizde, hem karada hem denizde yaşayanlar olarak gruplandırırız. Kitapları roman, ders kitabı, test kitabı gibi ayırırız.
TEK FONKSİYON
Grafiği orijine göre simetrik olan fonksiyonlar tek fonksiyondur.
- Tek fonksiyonda her x ∈ R için f(-x) = -f(x) sağlanır.
- Tek fonksiyonlarda x’in çift kuvvetlerinin olduğu terimlerin katsayıları sıfırdır.
ÇİFT FONKSİYON
Grafiği y eksenine göre simetrik olan fonksiyonlara çift fonksiyon denir.
- Çift fonksiyonlar her x ∈ R için f(-x) = f(x) olur.
- Çift fonksiyonlarda x’in tek kuvvetlerinin olduğu terimlerin katsayıları sıfırdır.
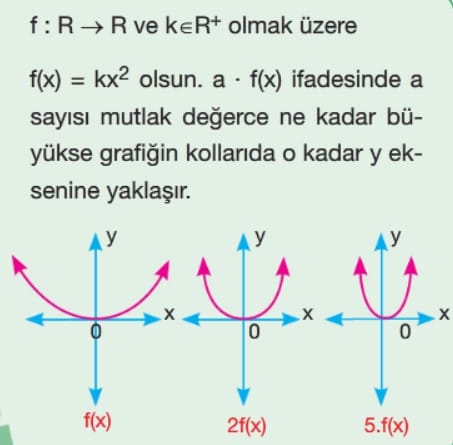
Bilgi: y = f(x) fonksiyonunun grafiği kullanılarak y = k . f(x) fonksiyonunun grafiği elde edilirken fonksiyonun x eksenini kestiği noktalar değişmez.
Bilgi: y = f(x) fonksiyonunun grafiği kullanılarak y = f(kx) fonksiyonunun grafiği oluşturulurken fonksiyonun y eksenini kestiği noktalar değişmez. Değişim tanım kümesinde olur.
Bilgi: y = f(x) fonksiyonunun grafiği ile y = |f(x)| fonksiyonunun grafiği elde edilirken f(x) fonksiyonunun grafiğinde x ekseninin altında kalan (fonksiyonun negatif değerler aldığı) kısımların x eksenine göre simetriği alınır.

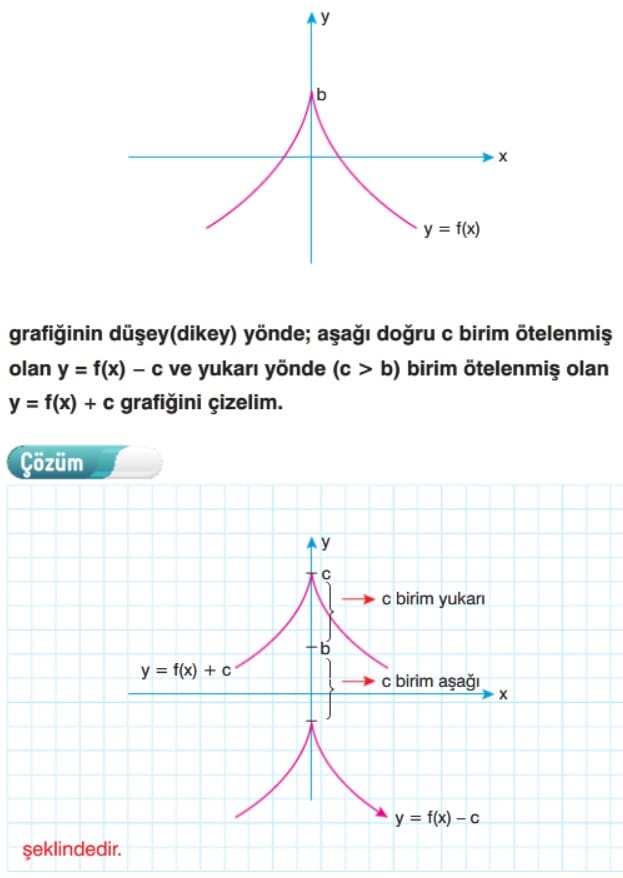
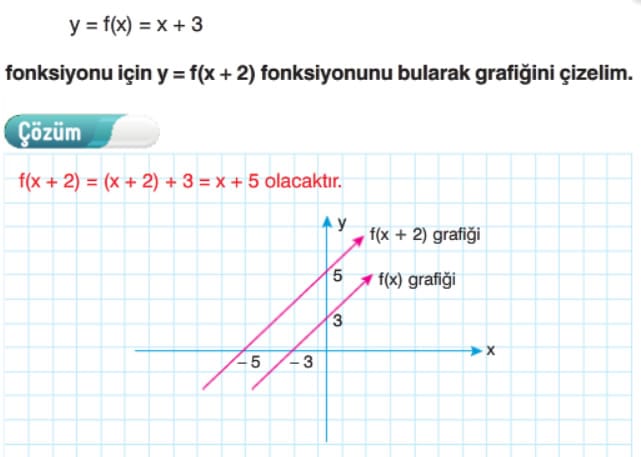
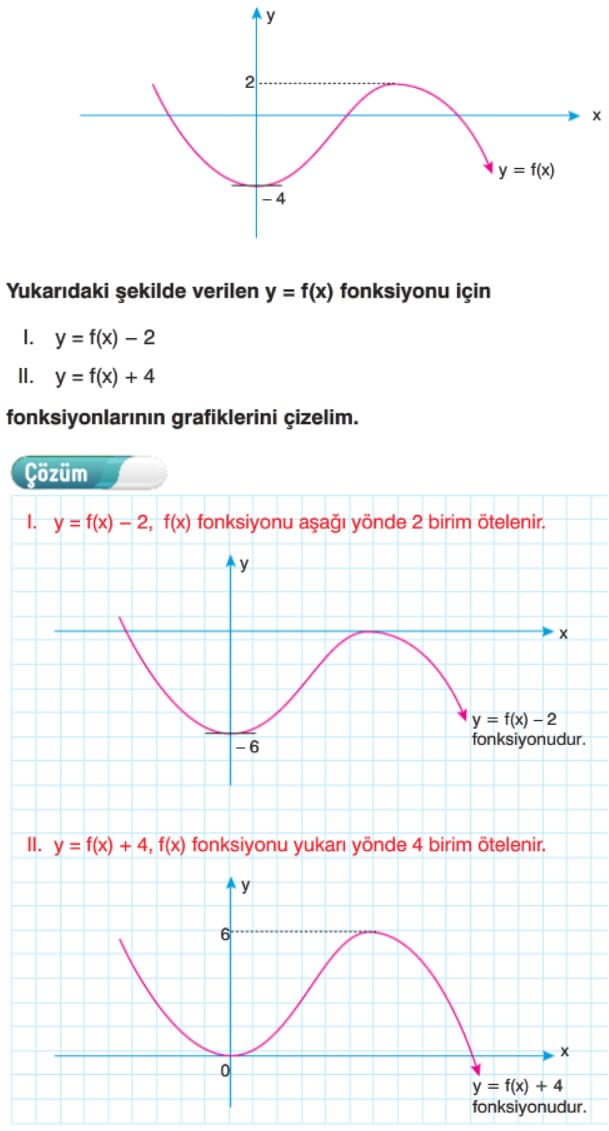












Çok faydalı kendi adıma çok teşekkür ederim 👍🏻