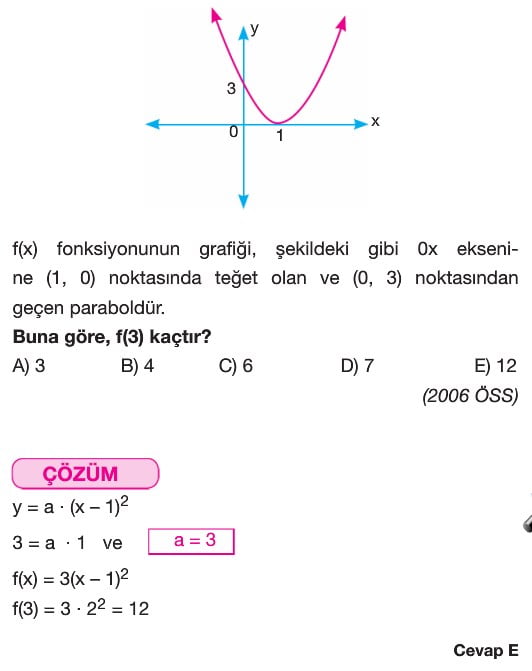
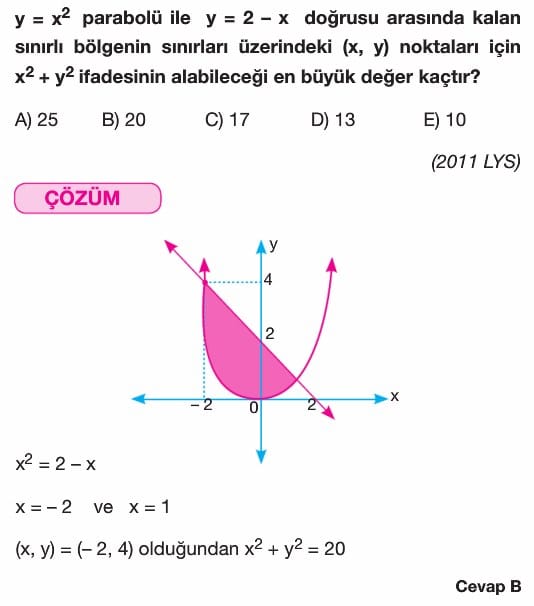
Fonksiyonlarda Uygulamalar 11. Sınıf
- Fonksiyonlarla İlgili Uygulamalar
- İkinci Dereceden Fonksiyonların Grafikleri (Parabol)
- Fonksiyonların Dönüşümleri
1. Fonksiyonlarla İlgili Uygulamalar
A) f(x) = ax + b şeklindeki fonksiyonların grafikleri ile ilgili uygulamalar
B) Fonksiyonun x-eksenini Kestiği Noktalar
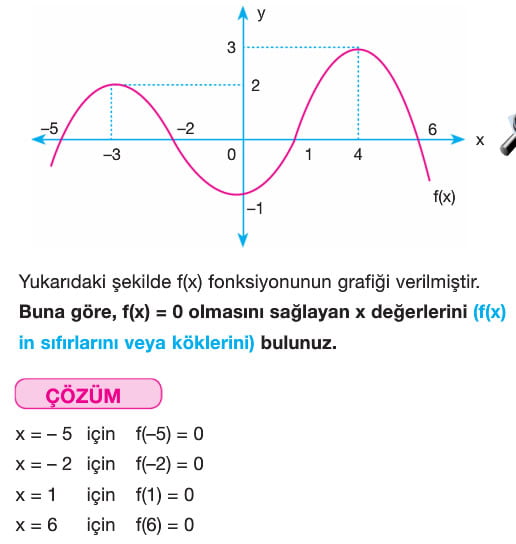
Bir k gerçek sayısı için f(k) = o oluyorsa k sayısına f fonksiyonunun kökü (sıfırı) denir.
Örneğin; f(x) = 2x – 6 fonksiyonunun köklerini bulalım.
f(x) = 0
2x – 6 = 0 ise x = 3
f(3) = 0 olduğundan fonksiyonun kökü 3 tür.
Dikkat: Bir f(x) fonksiyonunun kökleri (sıfırları) aynı zamanda fonksiyon grafiğinin x-eksenini kestiği noktalardır.
Örneğin; f(x) = 3x + 15 fonksiyonu x eksenini;
3x + 15 = 0 ⇒ x = -5 olduğundan x = -5 için keser.
Dikkat: Bir f(x) fonksiyonunun grafiği x eksenini kesmiyorsa f(x) fonksiyonunun sıfırlayanı yoktur. Bundan dolayı
f(x) = 0 denkleminin çözüm kümesi de boş kümedir.

C) Fonksiyonun y-eksenin Kestiği Noktalar
Bir f(x) fonksiyonunun y eksenini kestiği nokta x = 0 için (yani f(0)) bulunur.
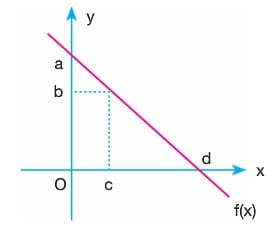
f(x) fonksiyonunun;
- x eksenini kestiği nokta (d, 0)
- y eksenini kestiği nokta (0, a)
şeklindedir.
Örneğin; f(x) = x2 + 5x + 7 fonksiyonunun y eksenini kestiği noktayı bulalım.
x = 0 için f(0) = 7 olur.
Dikkat: Bir f(x) fonksiyonu için;
f(0) = 0
oluyorsa “fonksiyon orjinden geçiyor” demektir.
Örnek:

Örnek:

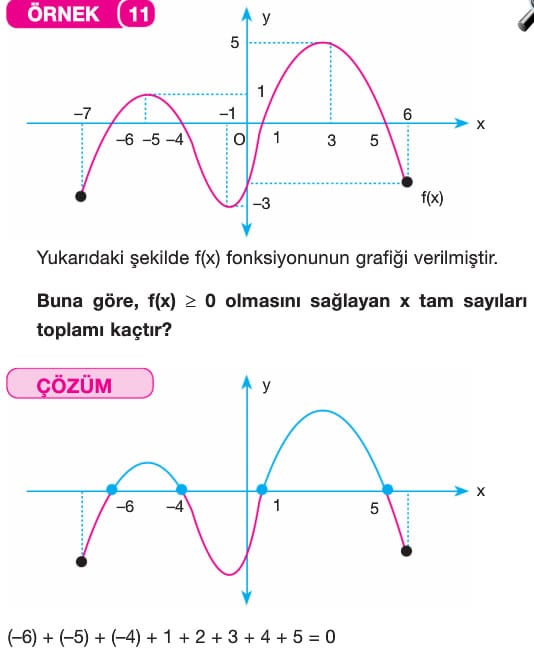
D) Fonksiyonun Pozitif veya Negatif Olması
Bir fonksiyon grafiğinde;
- Grafiğin x ekseninin üstünde olduğu aralıktaki x değeri için fonksiyon pozitif değerlidir.
- Grafiğin X ekseninin altında olduğu aralıktaki x değerleri için fonksiyon negatif değerlidir.

Örnek:
E) Fonksiyonun Artan ve Azalan Olması
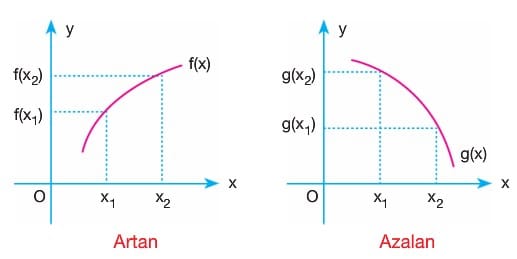
Bir f(x) fonksiyonunun tanım aralığındaki her x1 ve x2 değeri için;
- x1 < x2 için f(x1) < f(x2) oluyorsa fonksiyon artandır.
- x1 < x2 için f(x1) > f(x2) oluyorsa fonksiyon azalandır.
Örnek:
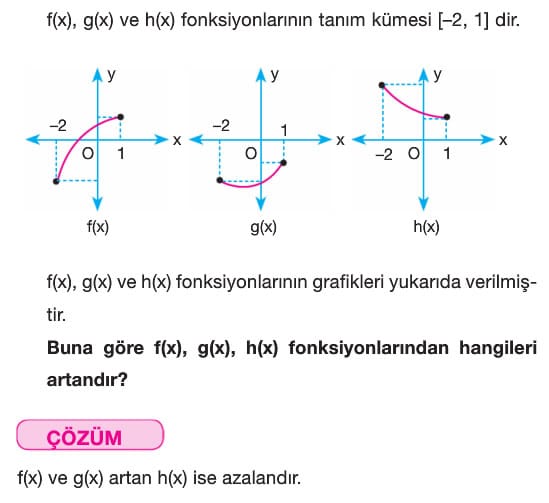
Örnek:

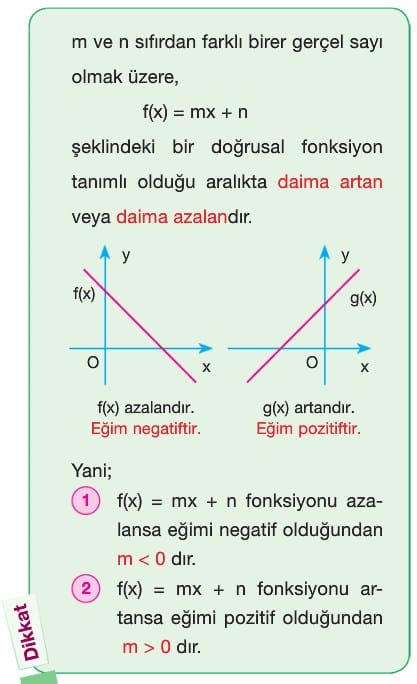
Örnek:
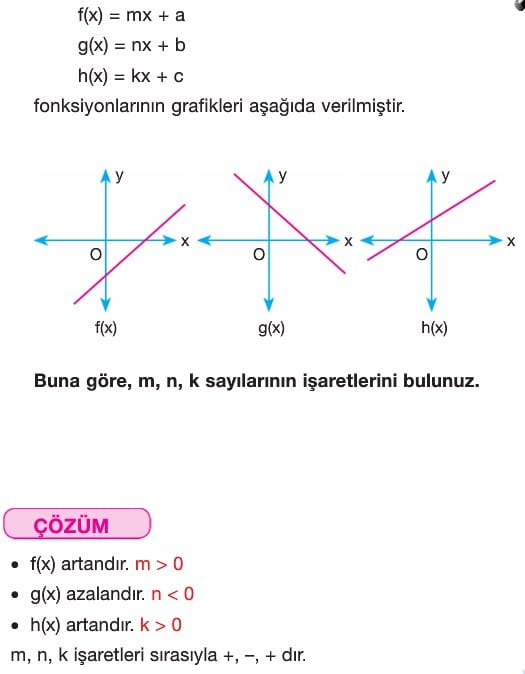
Örnek:

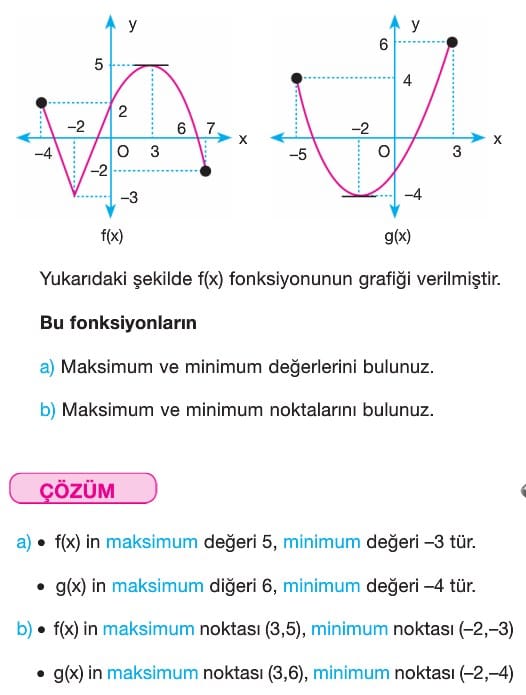
F) Fonksiyonun Maksimum ve Minimum (En Büyük ve En Küçük) Değeri
f: A → B ve f(x) bir fonksiyon olsun.
- xm ∈ A olmak üzere A kümesindeki bütün x elemanları için,
f(xm) > f(x)
oluyorsa f(xm) fonksiyonun maksimum (en büyük) değeridir. - xn ∈ A olmak üzere A kümesindeki bütün x elemanları için;
f(xn) < f(x)
oluyorsa f(xn) fonksiyonun minimum (en küçük) değeridir. Örneğin;
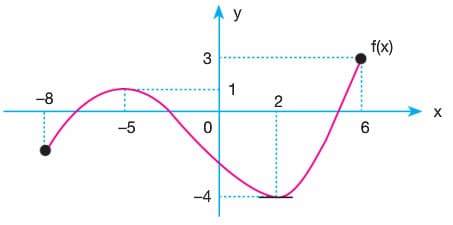
Şekilde verilen f(x) fonksiyonunun grafiğinde tanım kümesindeki her x değeri için f(x) in [-4, 3] aralığında değer aldığını görüyoruz. f(x) in;
- maksimum değeri = 3
- minimum değeri = -4
2. Ortalama Değişim Hızı
A) Ortalama Değişim Hızı

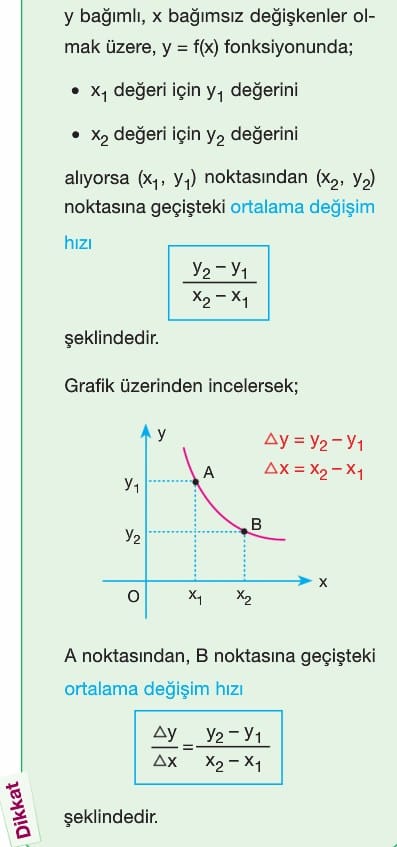
Dikkat:
- Ortalama değişim hızının negatif veya pozitif çıkması sadece değişimin yönünü gösterir.
- Ortalama değişim hızı mutlak değerce ne kadar büyükse değişim hızı da o kadar büyüktür.
B) Doğrusal Fonksiyonlarda Ortalama Değişim Hızı
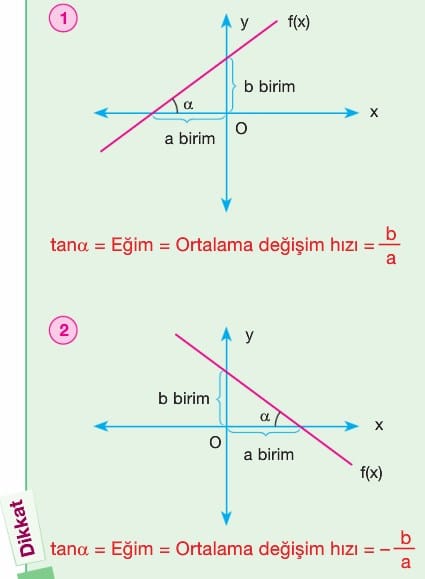
Örnek:

3. Parabol ve Parabol Çizimi
A) Parabol

Örnek:

Örnek:
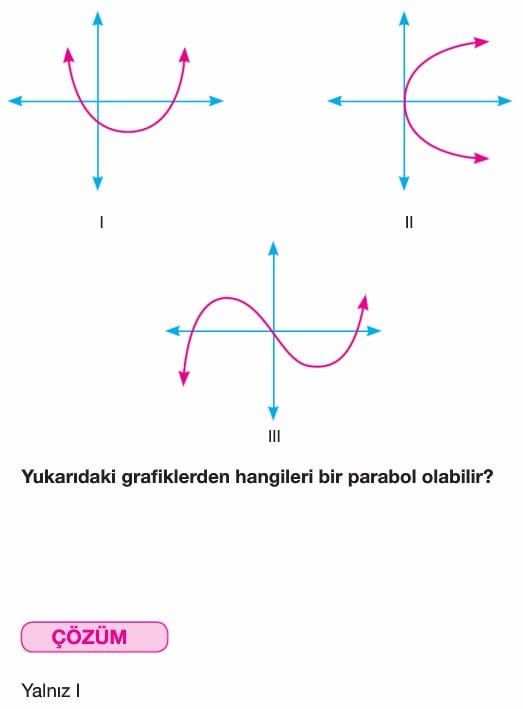

Örnek:

B) Grafik Çizimi
1) f(x) = ax2 fonksiyonunun grafiği
f(x) = ax2 ifadesi;
f(x) = a(x – 0)2 + 0 olduğundan tepe noktası (0, 0) olur.
Yani f(x) = x2 gibi fonksiyonların grafikleri daima orjinden geçer. Bu fonksiyonda x için verilecek değerlere karşılık f(x) in değerleri bulunur.
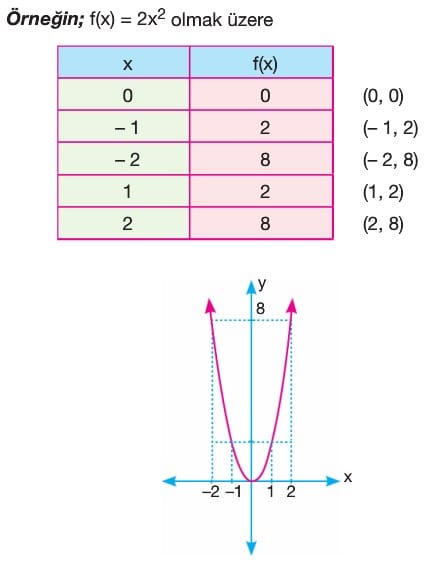
Örnek:
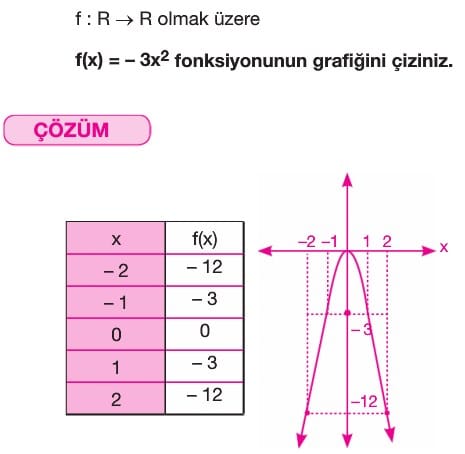

Örnek:
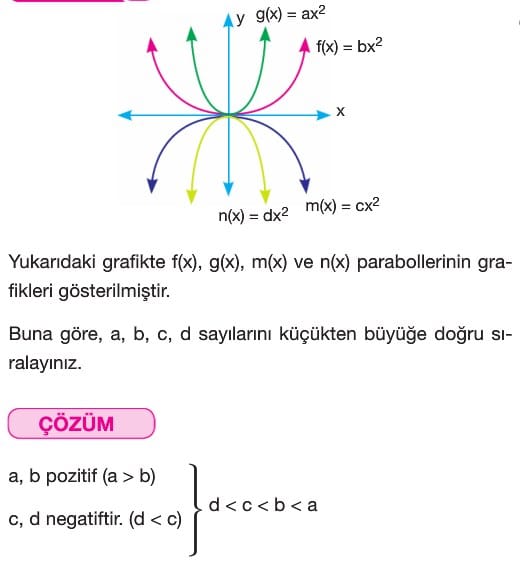
2. f(x) = ax2 + k fonksiyonunun grafiği
f(x) = ax2 fonksiyonunun grafiğini y ekseni üzerinde
- pozitif yönde k birim öteleyerek ax2 + k
- negatif yönde k birim öteleyerek ax2 – k
fonksiyonunun grafiği elde edilir.
Örnek:
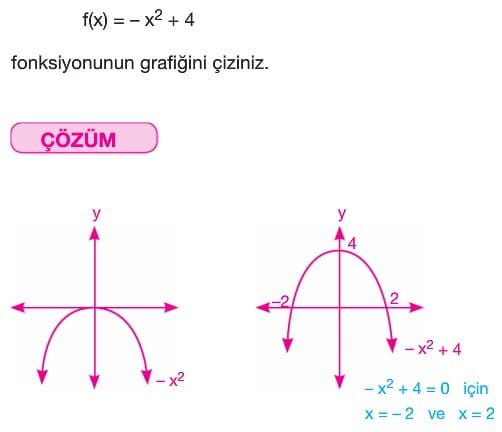
3. f(x) = a(x – r)2 fonksiyonunun grafiği
- f(x – r) fonksiyonunun grafiği, f(x) fonksiyonunun grafiğinin x ekseni üzerinde r birim pozitif yönde ötelenmesi ile
- f(x + r) fonksiyonunun grafiği, f(x) fonksiyonunun grafiğinin x ekseni üzerinde r birim negatif yönde ötelenmesi ile elde edilir.
O halde f(x) = a(x – r)2 fonksiyonunun grafiğinde f(x) = ax2 fonksiyonunun grafiğinin r birim pozitif yönde ötelenmesiyle elde edilir.
Dikkat: f(x)=a.(x-r)2+k
parabolünün tepe noktası koordinatlarının yani (r, k) nın bulunması ile de grafik çizilebilir. Burada f(x) = a(x – r)2 olduğundan k = 0 olur.
Dikkat: Bir parabolün y eksenini kestiği noktayı bulmak için fonksiyonda x = 0 yazılabilir.
Örnek:
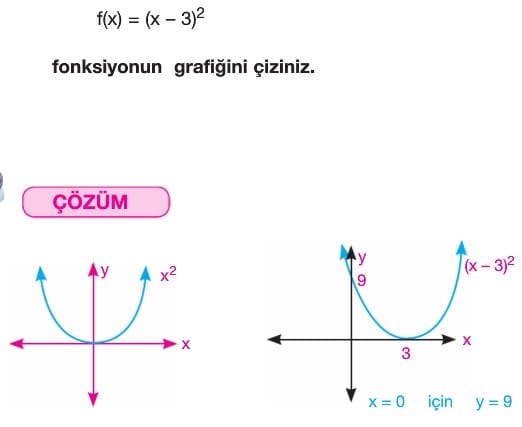
4. f(x) = a.(x – r)2 + k fonksiyonunun grafiği
f(x) = a.(x – r)2 + k grafiği f(x) fonksiyonunun grafiğinin
- x ekseni üzerinde pozitif yönde r kadar
- y ekseni üzerinde pozitif yönde k kadar
ötelemesi ile elde edilir.
Örnek:
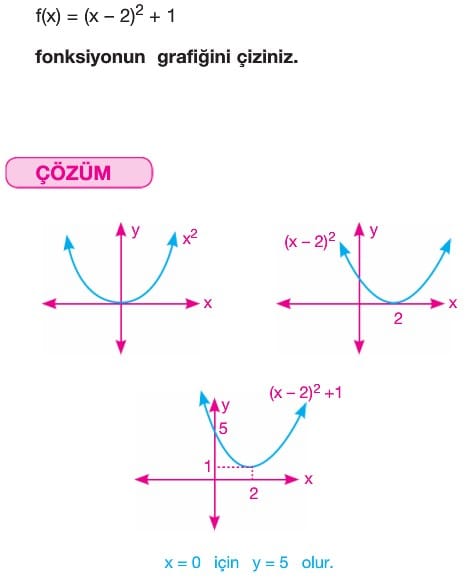
C) Tepe Noktası
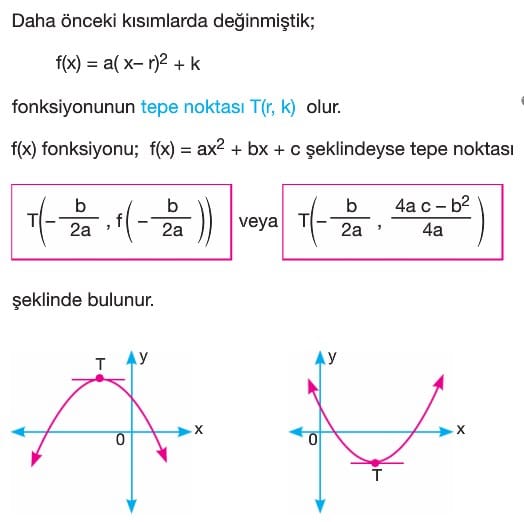
Örnek:

4. Simetri Ekseni – En Büyük ve En Küçük Değer
A) Simetri Ekseni
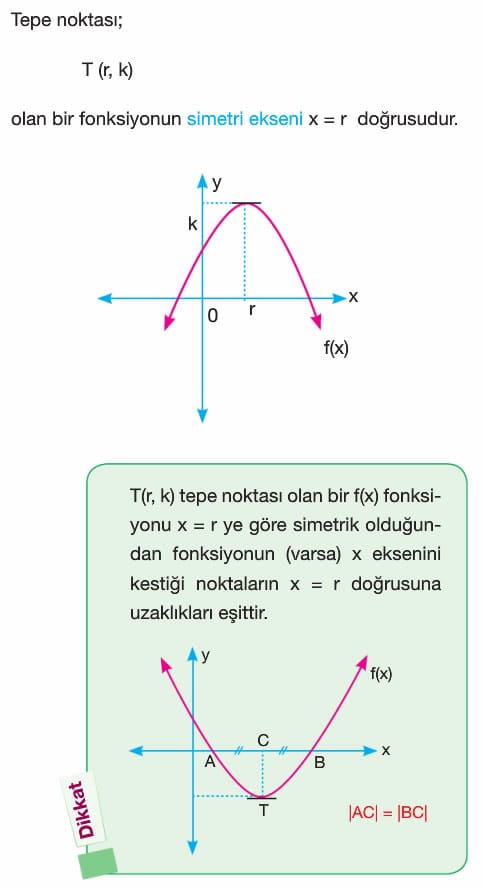
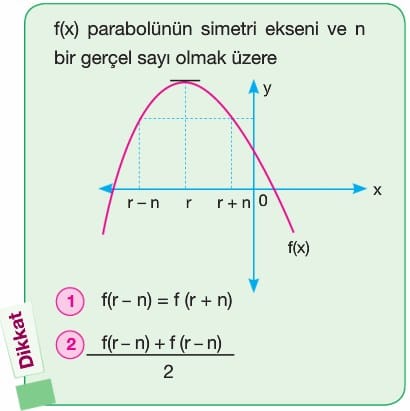
Örnek:

B) En Büyük ve En Küçük Değer (Maksimum ve Minimum)

Örnek:

Örnek:


Örnek:


Örnek:

5. f(x) = ax2+bx+c Formunda Verilen Paraboller
A) f(x) = ax2+bx+c parabolünün grafiği

Örnek:

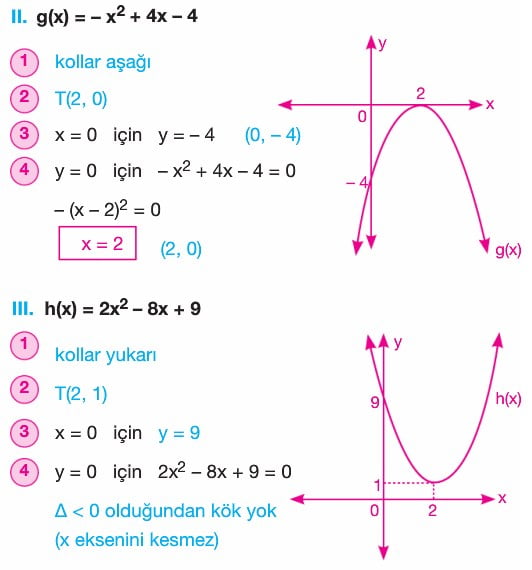

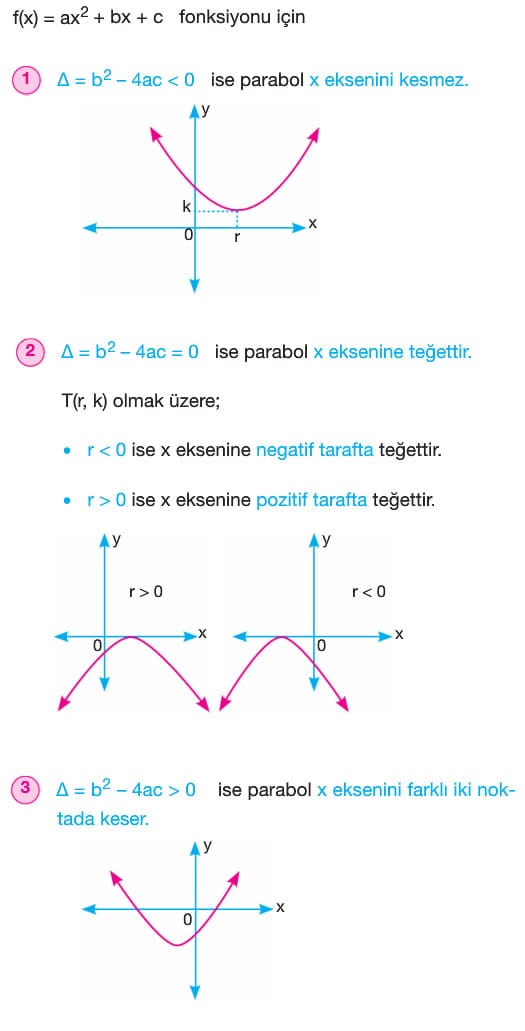
B) x Eksenini Kesme Durumu
C) y Eksenini Kesme Durumu
f(x) = ax2 + bx + c fonksiyonu için
- f(x) = ax2 + bx + c fonksiyonunun y eksenini kestiği nokta (O, c) noktasıdır.
- f(x) = ax2 + c fonksiyonunun y eksenini kestiği nokta (0, c) noktası olup, bu nokta aynı zamanda fonksiyonun tepe noktası koordinatıdır.
Örnek:

Örnek:
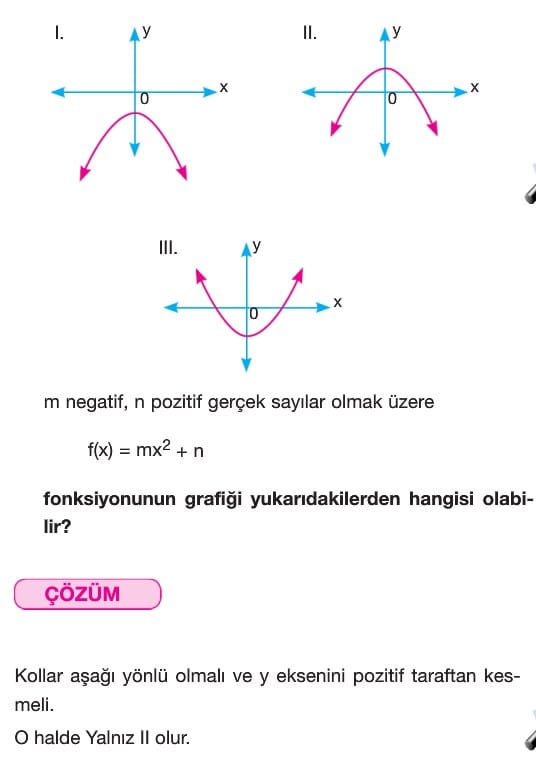
D) Katsayı İlişkileri
f(x) = ax2 + bx + c fonksiyonunda a, b, c katsayılarının işaretleri incelenirken;
- a nın işareti, kolların aşağı veya yukarı yönlü oluşana göre
- b nin işareti, T(r, k) noktasındaki r ye göre
- c nin işareti, y eksenini kestiği yere göre değerlendirilir.
Örnek:

6. Parabolün Fonksiyonunu Bulma, Grafiklerin Kesişimi
A) Tepe Noktası ve Bu nokta Dışında Başka Bir Noktası Belli Olan Paraboller

Örnek:
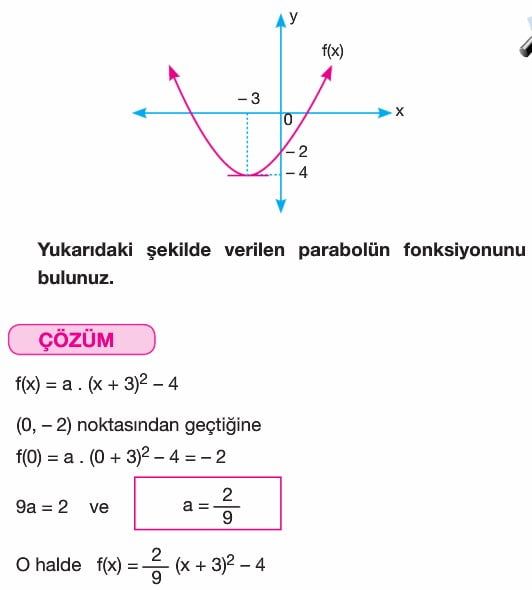
B) x Eksenin Kestiği Noktalar ve Bu Noktalar Dışında Başka Bir Noktası Belli Olan Paraboller
Bir parabol x eksenini (x1, 0) ve (x2, 0) noktalarında kesiyorsa fonksiyon
f(x) = a. (x – x1) . (x – x2) şeklindedir. Parabolün geçtiği diğer noktada kullanılarak a bulunur.
Örnek:

Örnek:
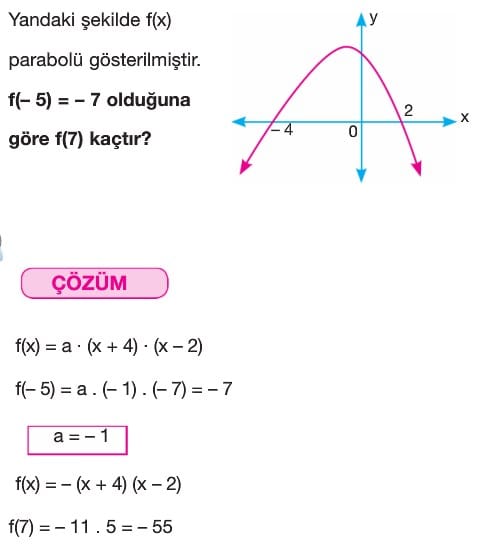
C) Birbirinden Farklı Herhangi Üç Noktası Belli Olan Paraboller

Örnek:

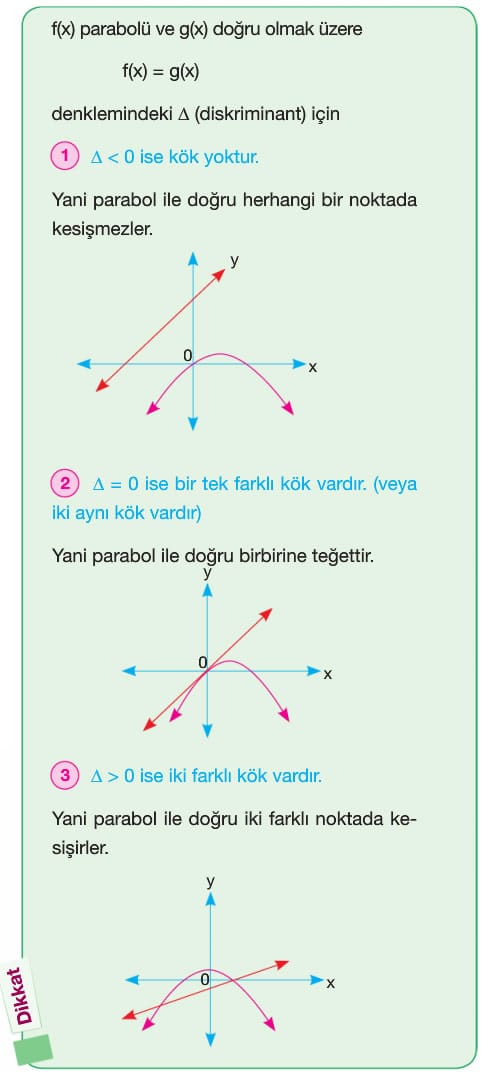
D) Parabol İle Doğrunun Kesişimi

7. Dönüşümler, Tek – Çift Fonksiyon
A) Dönüşümler
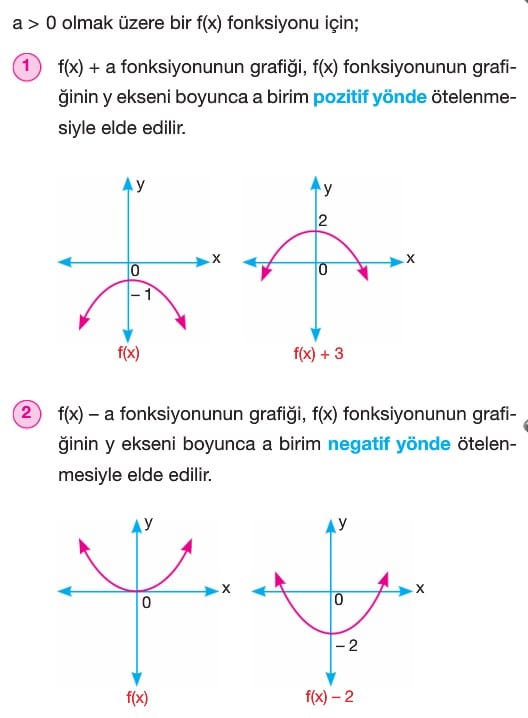
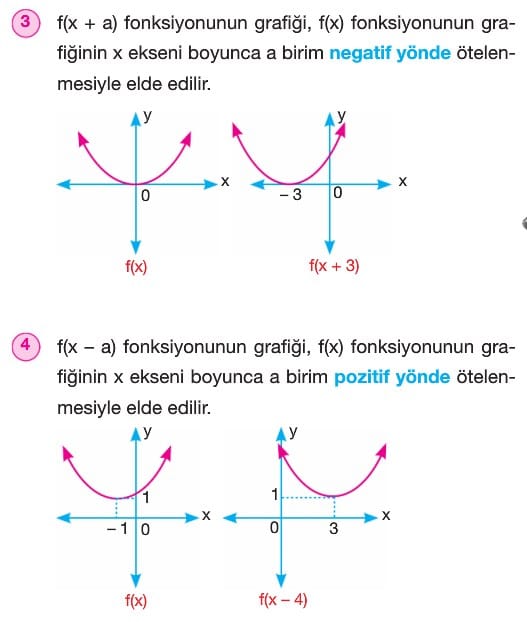
Örnek:
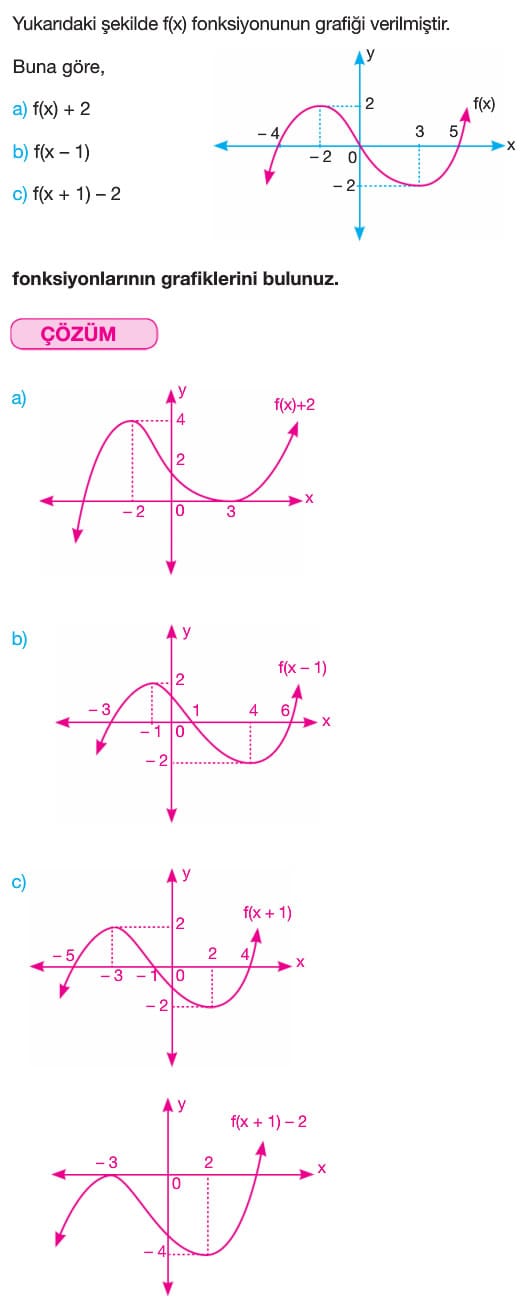
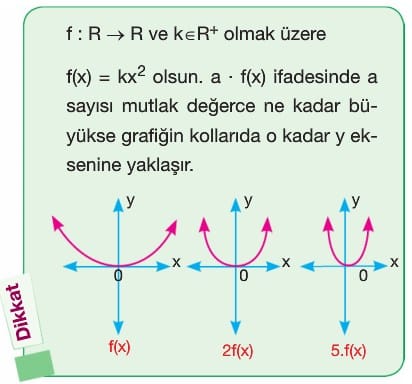
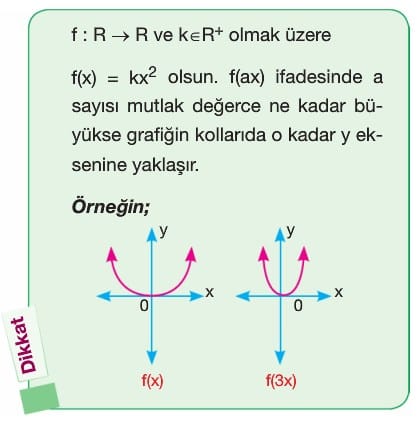
Örnek:
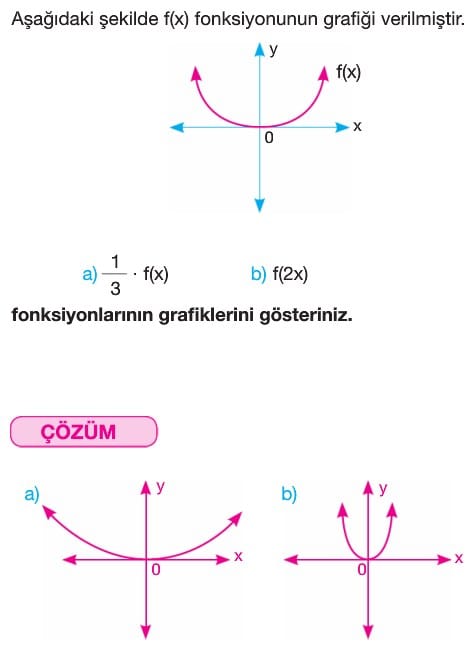
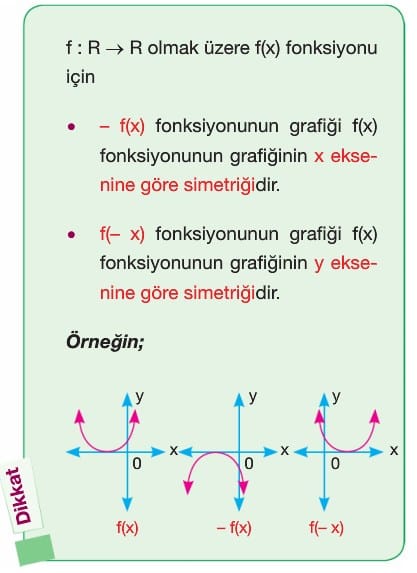
Örnek:
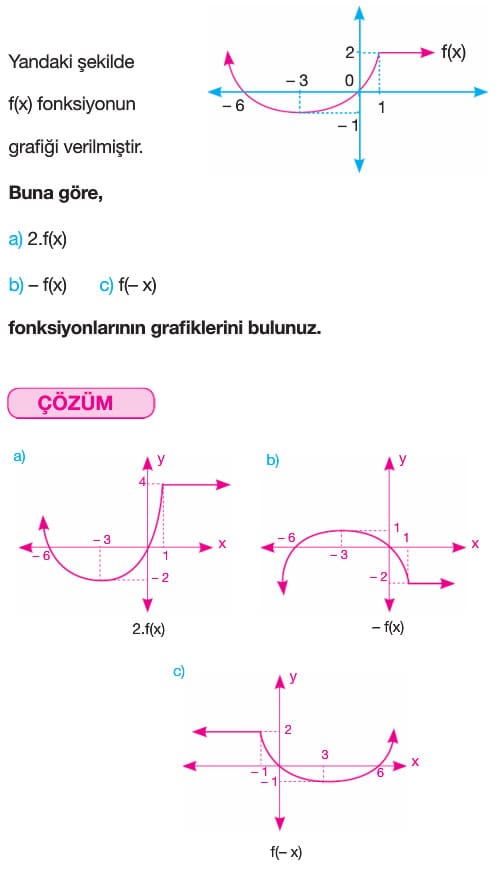

Örnek:

B) Tek ve Çift Fonksiyonlar

Örnek:


Örnek:
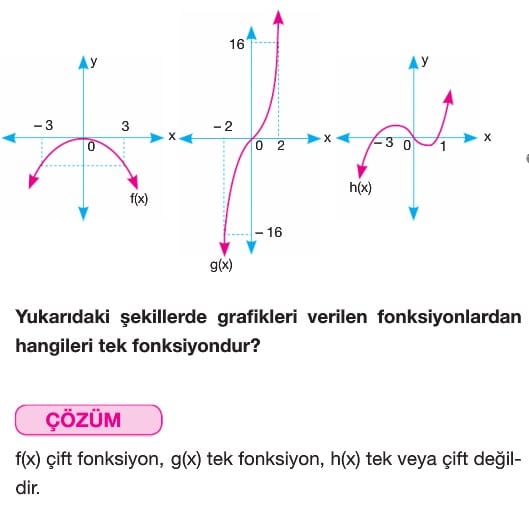
Örnek:

Çözümlü Örnek Test Soruları
Soru 1:
Bir f fonksiyonu tanımlı ve f(x) = 2x – 3 olduğuna göre, f(5) kaçtır?
A) 5
B) 7
C) 9
D) 10
E) 12
Çözüm:
f(x) = 2x – 3 olduğuna göre, x = 5 için f(5) değerini bulalım:
f(5) = 2(5) – 3 = 10 – 3 = 7
Cevap: B
Soru 2:
g(x) = x² + 4x + 4 fonksiyonunun x = -2 için değeri kaçtır?
A) 0
B) 2
C) 4
D) 6
E) 8
Çözüm:
g(x) = x² + 4x + 4 fonksiyonunda x = -2 yerine koyarsak:
g(-2) = (-2)² + 4(-2) + 4 = 4 – 8 + 4 = 0
Cevap: A
Soru 3:
f(x) = 3x + 1 ve g(x) = x – 2 fonksiyonları veriliyor. (f o g)(4) nedir?
A) 5
B) 6
C) 7
D) 8
E) 9
Çözüm:
(f o g)(x) = f(g(x)) olarak tanımlıdır.
g(4) = 4 – 2 = 2
Şimdi f(2) değerini bulalım:
f(2) = 3(2) + 1 = 6 + 1 = 7
Cevap: C
Soru 4:
f(x) = x² – 5x + 6 fonksiyonunun kökleri nelerdir?
A) 2 ve 3
B) 3 ve 4
C) 1 ve 6
D) 2 ve 4
E) 1 ve 5
Çözüm:
f(x) = x² – 5x + 6 fonksiyonunun köklerini bulmak için:
x² – 5x + 6 = 0 denklemini çözelim.
Bu ifadeyi çarpanlarına ayırırsak:
(x – 2)(x – 3) = 0
x = 2 ve x = 3
Cevap: A
Soru 5:
h(x) = 4x – 7 fonksiyonunda h(x) = 9 olduğunda x kaçtır?
A) 2
B) 3
C) 4
D) 5
E) 6
Çözüm:
h(x) = 4x – 7 olduğuna göre, h(x) = 9 için:
4x – 7 = 9
4x = 16
x = 4
Cevap: C
Soru 6:
Bir fonksiyon f(x) = x³ – 3x² + x + 2 olarak tanımlıdır. f(2) değeri kaçtır?
A) 0
B) 2
C) 4
D) 6
E) 8
Çözüm:
f(x) = x³ – 3x² + x + 2 fonksiyonunda x = 2 yerine koyarsak:
f(2) = (2)³ – 3(2)² + (2) + 2
= 8 – 12 + 2 + 2
= 0
Cevap: A
Soru 7:
f(x) = 2x + 3 ve g(x) = x – 1 fonksiyonları veriliyor. (g o f)(3) nedir?
A) 3
B) 5
C) 7
D) 8
E) 9
Çözüm:
(g o f)(x) = g(f(x)) olarak tanımlıdır.
f(3) = 2(3) + 3 = 6 + 3 = 9
Şimdi g(9) değerini bulalım:
g(9) = 9 – 1 = 8
Cevap: D
Soru 8:
f(x) = x² + 2 ve g(x) = 3x + 1 fonksiyonları veriliyor. (f o g)(2) nedir?
A) 25
B) 30
C) 35
D) 40
E) 45
Çözüm:
(f o g)(x) = f(g(x)) olarak tanımlıdır.
g(2) = 3(2) + 1 = 6 + 1 = 7
Şimdi f(7) değerini bulalım:
f(7) = 7² + 2 = 49 + 2 = 51
Cevap: E
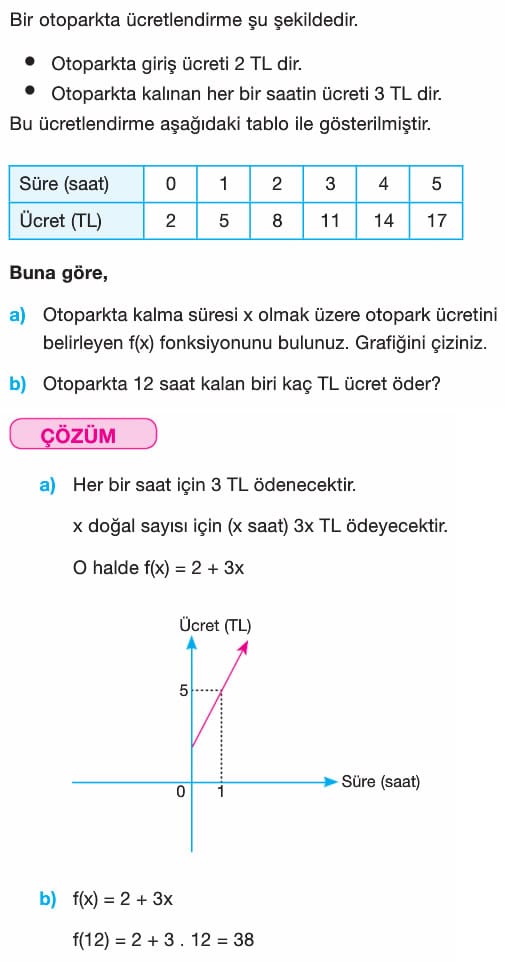
Soru: Bir Otoparkta ücretlendirme şu şekildedir.
° Otoparkta giriş ücreti 2 TL dir.
° Otoparkta kalınan her bir saatin ücreti 3 TL dir.
Bu ücretlendirme aşağıdaki tablo ile gösterilmiştir.
Buna göre,
a) Otoparkta kalma süresi X olmak üzere otopark ücretini belirleyen f(x) fonksiyonunu bulunuz. Grafiğini çiziniz.
b) Otoparkta 12 saat kalan biri kaç TL ücret öder?
Soru: Yukarıdaki şekilde, bir markette satılan A ve B ürünlerine ait alış – satış fiyatlarını veren grafik gösterilmiştir.
a) A ürününe ait alış – satış ilişkisini veren fonksiyonu bulunuz.
b) B ürününe ait alış – satış ilişkisini veren fonksiyonu bulunuz.
c) A ürününden elde edilen kâr oranını bulunuz.
d) B ürününden elde edilen zarar oranını bulunuz.
Soru: Yukarıdaki grafikte, içinde bir miktar su bulunan bir havuzun, havuzu dolduran musluğun açılmasıyla birlikte, içindeki su miktarının zamana göre değişimi gösterilmiştir.
a) Zamana göre bu havuzdaki su miktarını veren fonksiyonu bulunuz.
b) 10. saatte havuzda kaç ton su vardır?
c) Kaçıncı saatte havuzda 120 ton su bulunur?
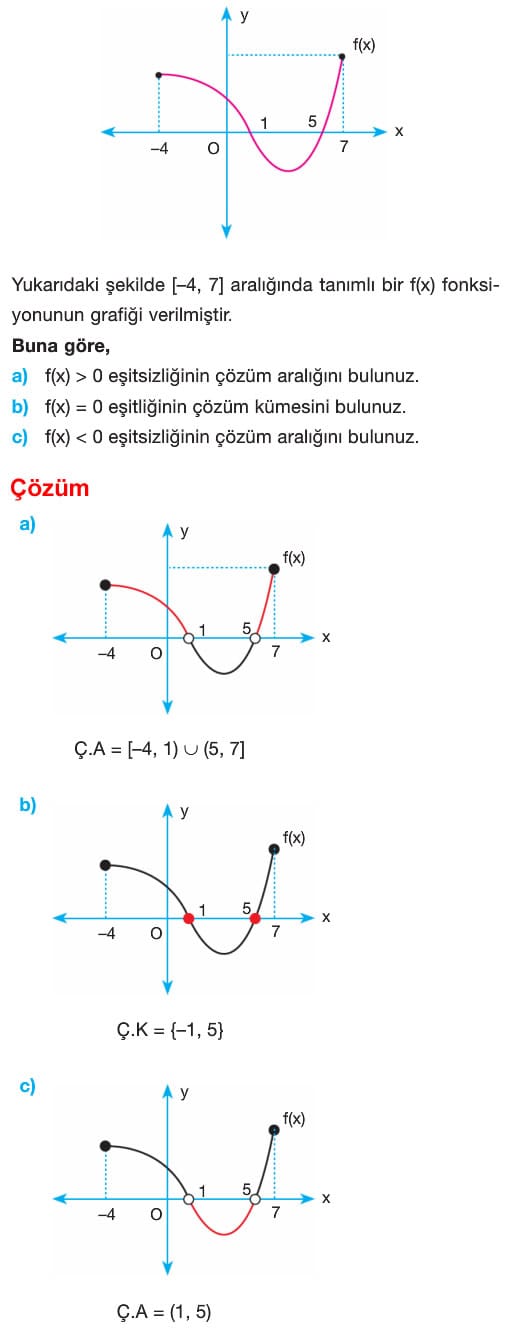
Örneğin; yanda grafiği verilen f(x) fonksiyonunda;x = 4 için f(-4) = 3 olur. Yani pozitif bir değer alır. O halde şekilden görebileceğimiz gibi [-4, 3) aralığındaki bütün x değerleri için f(x) pozitif değerlidir (f(x) > 0 olur.). x = 3 için f(3) = 0 olur. (3, 5] aralığındaki bütün değerler için f(x) negatif olur (f(x) < 0 olur.). Şekilden görebileceğimiz gibi f(5) = -3 tür.