Fonksiyon Kavramı 10. sınıf
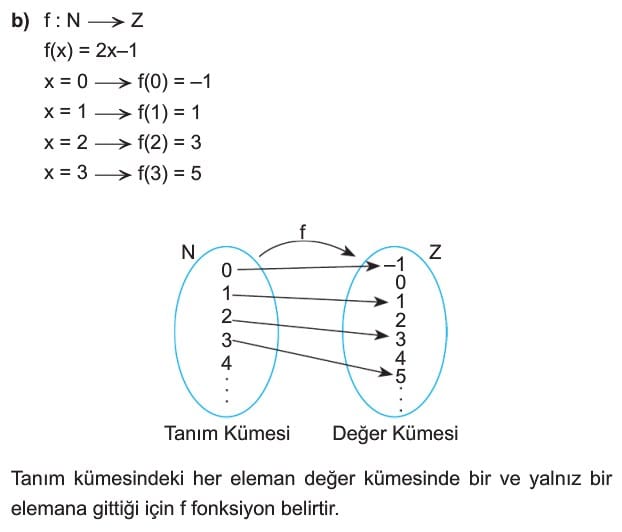
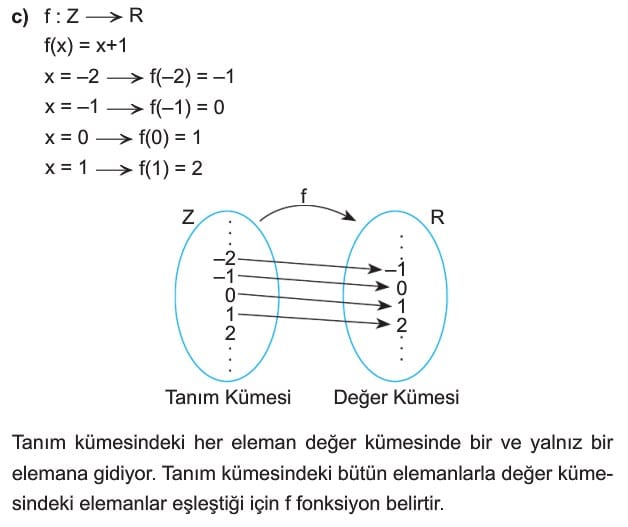
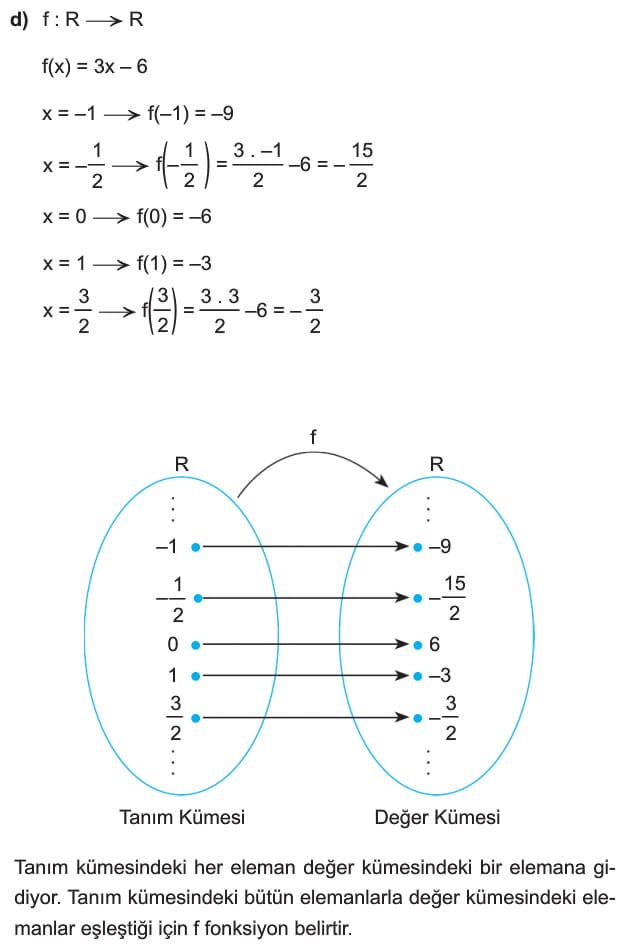
Boş kümeden farklı A ve B kümeleri için A nın her bir elemanını B nin bir tek elemanı ile eşleyen kurala A dan B ye fonksiyon denir ve genellikle f, g, h, veya F, G, H, sembolleriyle gösterilir.
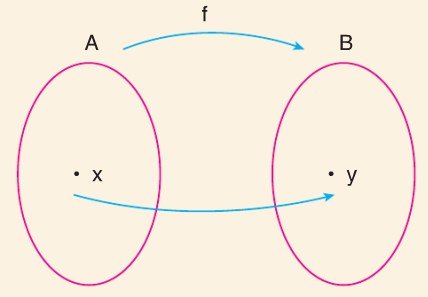
Yukarıda Venn şemasıyla gösterimde x ∈ A elemanın, y ∈ B elemanına eşleyen kural f ile gösterilmiştir. Bunu
f: A → B biçiminde ifade ederiz ve B deki y elemanı A daki x elemanına f kuralı ile bağlıdır deriz. Yani
f: A → B
x → y
x in f kuralı altındaki görüntüsü y dir denir.
Bunu f(x) = y şeklinde de gösteririz.
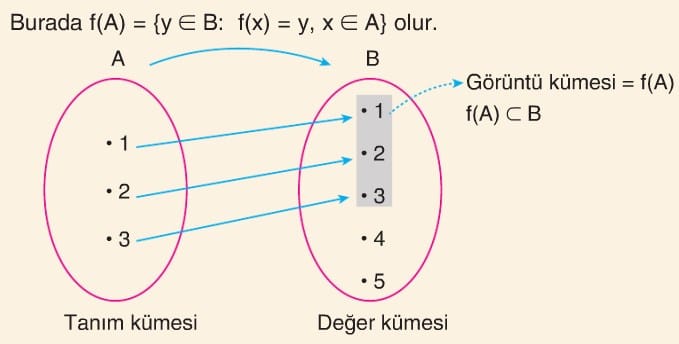
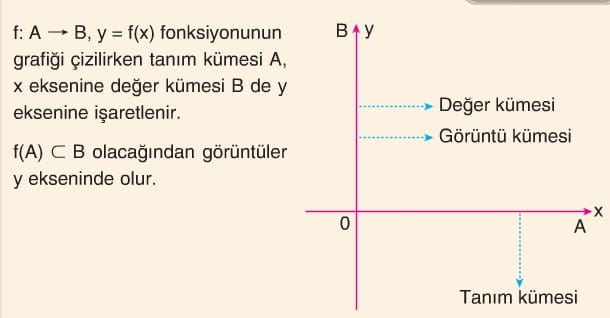
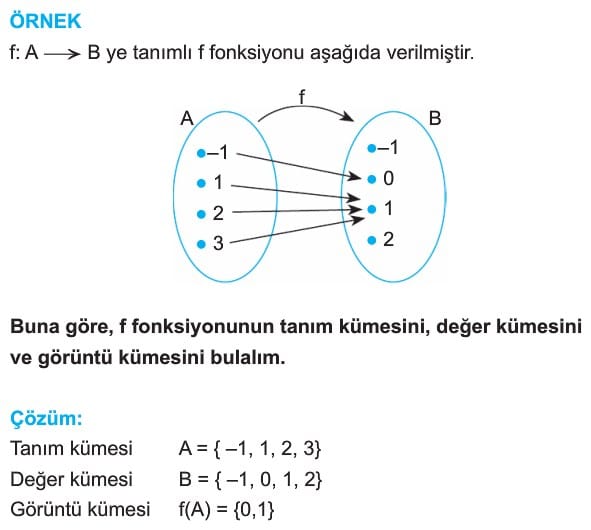
f: A → B gösteriminde A ya fonksiyonun tanım kümesi B ye fonksiyonun değer kümesi denir. Tanım kümesinin f kuralı altındaki görüntülerinin oluşturduğu f(A) kümesine de görüntü kümesi denir.
Dikkat: f: A → B, y = f(x) gösteriminde x’e bağımsız değişken, y’ye bağımlı değişken denir.
Fonksiyon Kavramı Soru Çözümleri
Fonksiyon Kavramı ve Gösterimi
- Fonksiyon Kavramı
- Fonksiyon Türleri
- Fonksiyonlarda Dört İşlem
- Fonksiyonların Grafikleri
- Doğrusal Fonksiyonlarla Modellenebilen Günlük Hayat durumları
İki Fonksiyonun Bileşkesi ve Bir Fonksiyonun Tersi
Çözümlü Örnek Test Soruları
Soru 1:
Bir fonksiyon tanımı, hangi iki küme arasındaki bağıntıyı ifade eder?
A) Sayılar ve harfler
B) Tanım kümesi ve değer kümesi
C) X ekseni ve Y ekseni
D) Doğrular ve düzlemler
Çözüm: Bir fonksiyon, tanım kümesindeki her bir elemanı değer kümesindeki bir elemana eşleyen bir bağıntıdır.
Cevap: B
Soru 2:
f(x) = 2x + 3 fonksiyonu için f(5) değeri kaçtır?
A) 10
B) 12
C) 13
D) 14
Çözüm: f(x) = 2x + 3 olduğuna göre, f(5) = 2(5) + 3 = 10 + 3 = 13 olur.
Cevap: C
Soru 3:
Bir fonksiyonun tanım kümesi A = {1, 2, 3} ve değer kümesi B = {4, 5, 6} ise, fonksiyonun eleman sayısı en fazla kaç olabilir?
A) 1
B) 2
C) 3
D) 4
Çözüm: Tanım kümesinde 3 eleman olduğundan, her bir eleman bir kez eşlenecektir, bu nedenle en fazla 3 eşleme yapılabilir.
Cevap: C
Soru 4:
f(x) = x² – 4 fonksiyonunun tanım kümesi R olduğunda, f(x) fonksiyonunun görüntü kümesi nedir?
A) R+
B) R
C) R-
D) [0, ∞)
Çözüm: f(x) = x² – 4 fonksiyonu tüm reel sayılarda tanımlıdır ve en küçük değeri -4 olur. Bu nedenle görüntü kümesi [-4, ∞) aralığıdır.
Cevap: D
Soru 5:
g(x) = 3x – 2 fonksiyonunun ters fonksiyonu g⁻¹(x) aşağıdakilerden hangisidir?
A) g⁻¹(x) = (x + 2) / 3
B) g⁻¹(x) = 3x + 2
C) g⁻¹(x) = (x – 2) / 3
D) g⁻¹(x) = -3x + 2
Çözüm: g(x) = 3x – 2 olduğundan, x = 3y – 2 ifadesiyle ters fonksiyonu y = (x + 2) / 3 olarak bulunur.
Cevap: A
Soru 6:
Aşağıdakilerden hangisi bir fonksiyon değildir?
A) Her öğrenciye bir numara eşleme
B) Her ülkeye başkent eşleme
C) Her kişiye bir kimlik numarası eşleme
D) Her ay bir mevsim eşleme
Çözüm: Aylar birden fazla mevsime denk gelebileceğinden, bu bir fonksiyon değildir.
Cevap: D
Soru 7:
f(x) = |x – 3| fonksiyonunun tanım kümesi ve görüntü kümesi nedir?
A) Tanım kümesi R, görüntü kümesi [0, ∞)
B) Tanım kümesi R+, görüntü kümesi R
C) Tanım kümesi [-3, ∞), görüntü kümesi R
D) Tanım kümesi R, görüntü kümesi R
Çözüm: Mutlak değer fonksiyonları için tanım kümesi R, görüntü kümesi [0, ∞) olur.
Cevap: A
Soru 8:
Bir fonksiyon f(x) = ax + b biçiminde verildiğinde, fonksiyonun eğimi nasıl bulunur?
A) a değeri
B) b değeri
C) x değeri
D) a + b
Çözüm: Doğrusal fonksiyonlarda eğim, x’in katsayısı olan a ile temsil edilir.
Cevap: A
A ve B boş kümeden farklı kümeler olmak üzere A kümesinin her elemanı B kümesinin bir ve yalnız bir elemanına eşleyen ilişkiye A dan B ye bir fonksiyon denir ve f A dan B ye ile gösterilir. Burada A kümesi tanım kümesi, B kümesi de değer kümesidir.
Günlük hayatımızdaki bir çok durum kendisi dışındaki durumlara bağlı olarak değişir. Hareket halindeki bir aracın deposundaki yakıtın zamana bağlı değişimi, manavdan alınan domatesin fiyatının alınan miktara bağlı değişimi bu durumlara örnek olarak verilebilir. Hayatımızdaki bu durumlara benzer sayısız çokluktaki durumları fonksiyon kavramını kullanarak matematiksel olarak ifade edebiliriz. Bu ünitede fonksiyon ile ilgili kavramlar, fonksiyonların farklı ifade biçimlerini, fonksiyon türlerini ve onları nasıl kullanabileceğimizi öğreneceğiz.
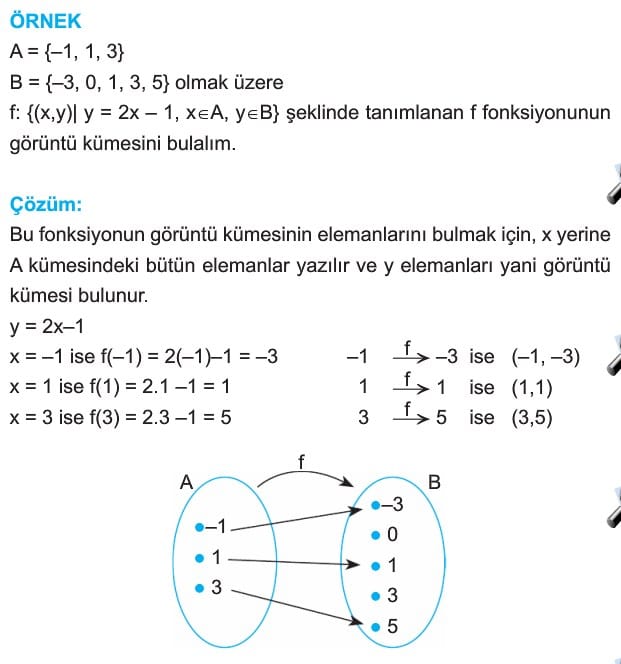
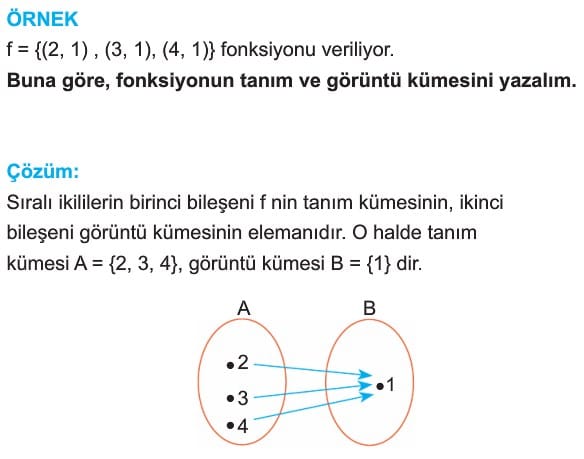
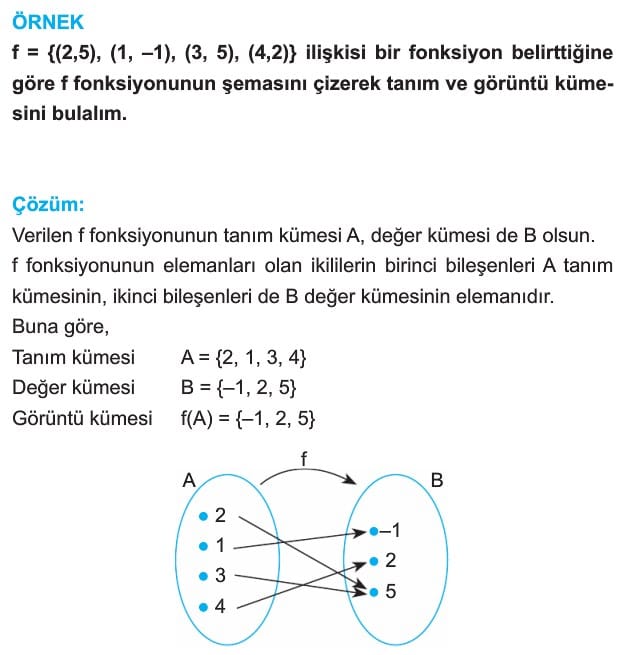
Örnek: f = {(2, 5), (1, -1), (3, 5), (4, 2)} ilişkisi bir fonksiyon belirttiğine göre f fonksiyonunun şemasını çizerek tanım ve görüntü kümesini bulalım.
Çözüm: Verilen f fonksiyonunun tanım kümesi A, değer kümesi B olsun. f fonksiyonunun elemanları olan ikililerin birinci bileşenleri A tanım kümesinin, ikinci bileşenleri de B değer kümesinin elemanlarıdır. Buna göre Tanım kümesi A = {2,1,3,4}, değer kümesi B = {-1,2-5}, görüntü kümesi f(A) = {-1, 2, 5}
Sıra Sizde: Dini bayramlar yakınların bir araya toplandığı, küçük aile bireylerinin büyüklerinin ellerini öptüğü aile birliğinin öneminin kavrandığı zamanlardır. Bir ailenin 2 çocuğu, bayramda dede ve ninelerinin ellerini öpecektir. Buna göre torunların ellerini öptüğü dede ve ninelerine eğlendiği ilişkinin bir fonksiyon olup olmadığını inceleyiniz.


















Çok yararlı oldu teşekürler