Eşkenar dörtgen ve Özellikleri, Eşkenar Dörtgende Alan 10. Sınıf

10. sınıf Matematik Konuları Konu Anlatımları Matematik

17.02.2025

Bütün kenar uzunlukları birbirine eşit olan paralelkenara eşkenar dörtgen denir.

EŞKENAR DÖRTGENİN ÖZELLİKLERİ

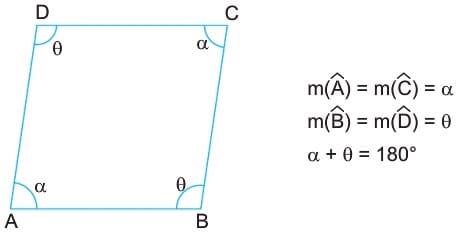
1. Paralelkenarda olduğu gibi karşılıklı açılar eşit, komşu açılar ise birbirinin bütünleridir.

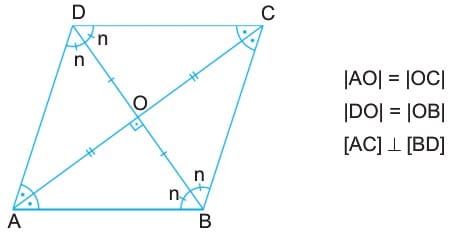
2. Köşegenler birbirini ortalar, köşegenler birbirine diktir ve köşegenler açıortaydır.

Çözümlü Sorular

EŞKENAR DÖRTGENDE ALAN

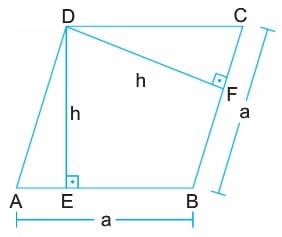
Eşkenar dörtgenin alanı, paralelkenarda olduğu gibi bir kenar uzunluğu ile o kenara ait yüksekliğin çarpımına eşittir.
A(ABCD) = |AB| . |DE| veya
A(ABCD) = |BC| . |DF| ile bulunur.

Ayrıca, eşkenar dörtgenin köşegenleri birbirine dik olduğundan, köşegen uzunluklarının çarpımının yarısı alanı verir. Buna göre,

A(ABCD) = AC.BD2 dir.

Çözümlü Sorular

Eşkenar Dörtgen Şenol Hoca

Eşkenar Dörtgen Hocalara Geldik

Eşkenar Dörtgen Ekol Hoca

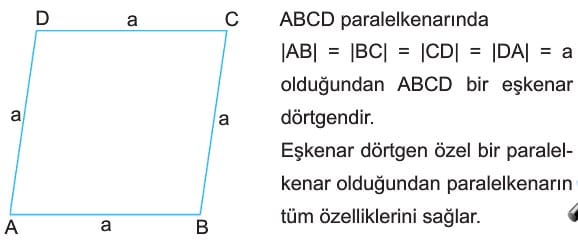
ABCD paralelkenarında |AB| = |BC| = |CD| = |DA| = a olduğundan ABCD bir eşkenar dörtgendir. Eşkenar dörtgen özel bir paralelkenar olduğundan paralelkenarın tüm özelliklerini sağlar.
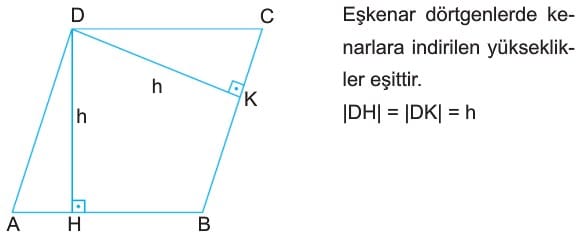
Eşkenar dörtgenlerde kenarlara indirilen yükseklikler eşittir. |DH| = |DK| = h

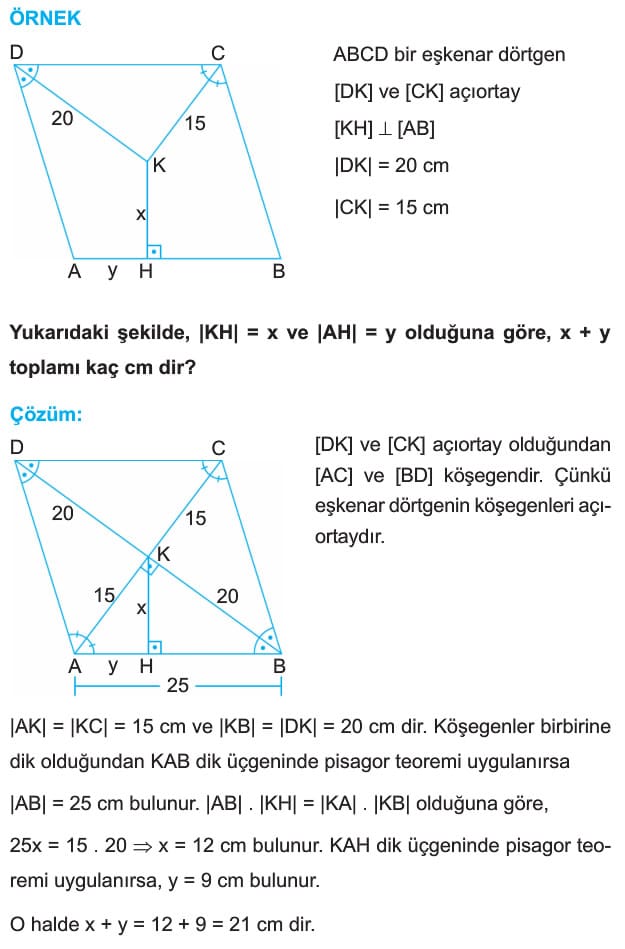
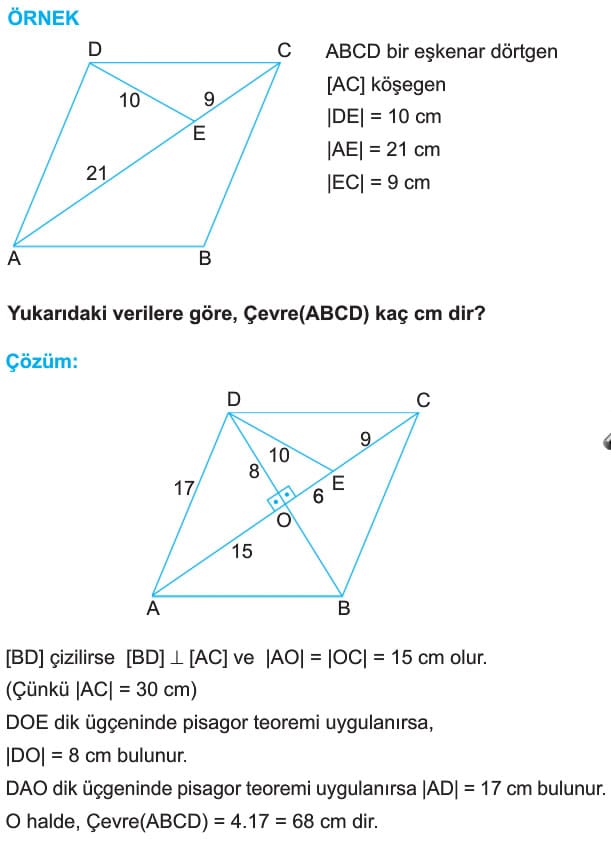
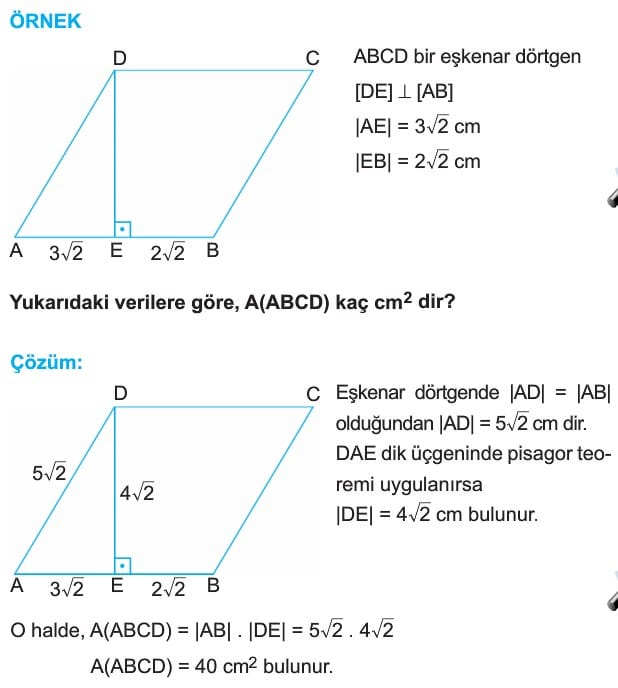
ÖRNEK: ABCD bir eşkenar dörtgen
[DK] ve [CK] açıortay
[KH] dik [AB]
|DK| = 20 cm
|CK| = 15 cm
Yukarıdaki şekilde, |KH| = x ve |AH| = y olduğuna göre, x + y toplamı kaç cm dir?
Çözüm: [DK] ve [CK] açıortay olduğundan [AC] ve [BD] köşegendir. Çünkü eşkenar dörtgenin köşegenleri açıortaydır.
|AK| = |KC| = 15 cm ve |KB| = |DK| = 20 cm dir. Köşegenler birbirine dik olduğundan KAB dik üçğeninde pisagor teoremi uygulanırsa
|AB| = 25 cm bulunur. |AB| . |KH| = |KA| . |KB| olduğuna göre,
25x = 15 . 20 ise x = 12 cm bulunur. KAH dik üçğeninde pisagor teoremi uygulanırsa, y = 9 cm bulunur.
O halde x+y=12+9=21 cm dir.

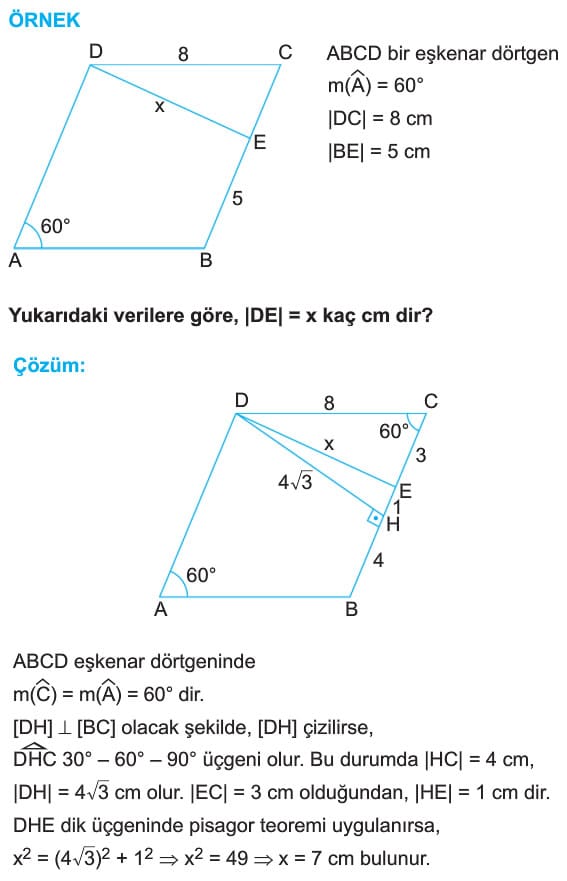
ÖRNEK: ABCD bir eşkenar dörtgen
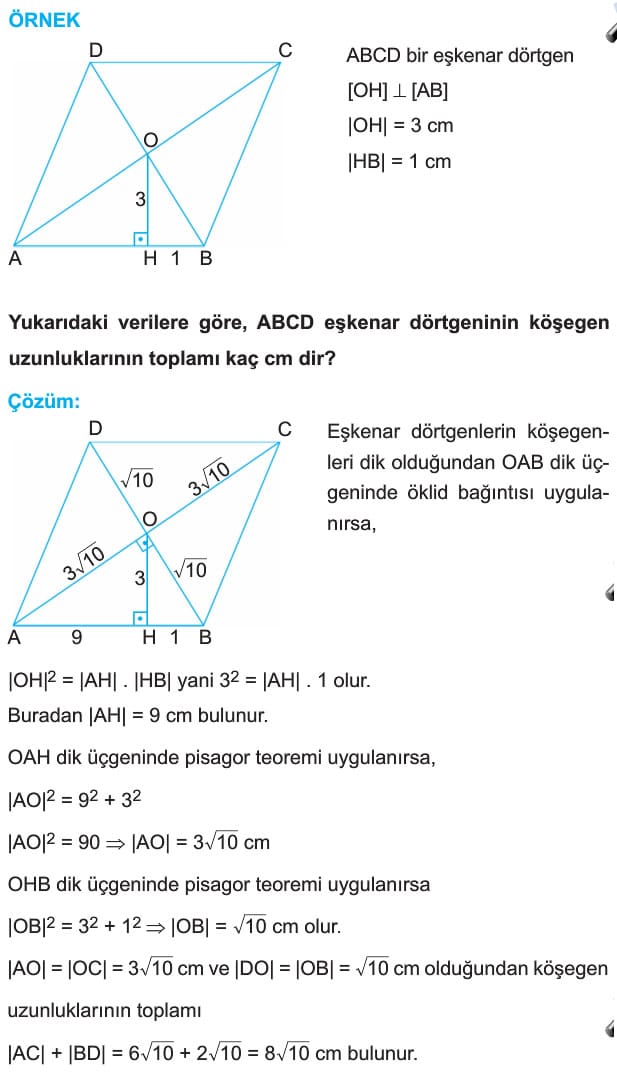
[OH] dik [AB], |OH| = 3 cm, |HB| = 1 cm
Yukarıdaki verilere göre, ABCD eşkenar dörtgeninin köşegen uzunluklarının toplamı kaç cm dir?
Çözüm: Eşkenar dörtgenlerin köşegenleri dik olduğundan OAB dik üçgeninde öklid bağıntısı uygulanırsa,
|OH|2 = |AH| . |HB| yani 3² = |AH| . 1 olur. Buradan |AH| = 9 cm bulunur. OAH dik üçğeninde pisagor teoremi uygulanırsa,
|AO|² = 9² + 3²
|AO|² = 90 ise |AO| = √90 = 3.√10 cm
OHB dik üçğeninde pisagor teoremi uygulanırsa
|OB|² = 3² +1² ise |OB| = √10 cm olur.
|AO| = |OC| = 3√10 cm ve |DO| = |OB| = √10 cm olduğundan köşegen uzunluklarının toplamı
|AC| + |BD| = 6√10 + 2√10 = 8√10 cm bulunur.

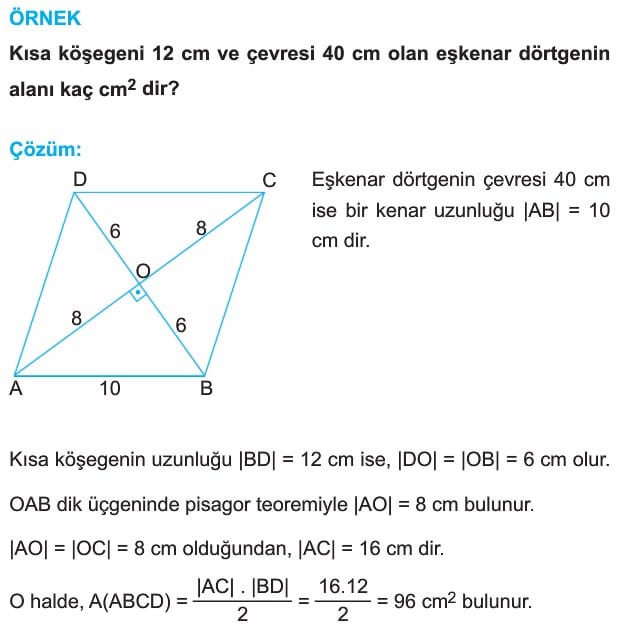
ÖRNEK: Kısa köşegeni 12 cm ve çevresi 40 cm olan eşkenar dörtgenin alanı kaç cm2 dir?
Çözüm: Eşkenar dörtgenin çevresi 40 cm ise bir kenar uzunluğu |AB| = 10 cm dir.
Kısa köşegenin uzunluğu |BD| = 12 cm ise, |DO| = |OB| = 6 cm olur.
OAB dik Üçgeninde pisagor teoremiyle |AO| = 8 cm bulunur.
|AO| = |OC| = 8 cm olduğundan, |AC| = 16 cm dir.
O halde, A(ABCD) = |AC| . |BD| / 2 = 16 . 12 / 2 = 96 cm² bulunur.

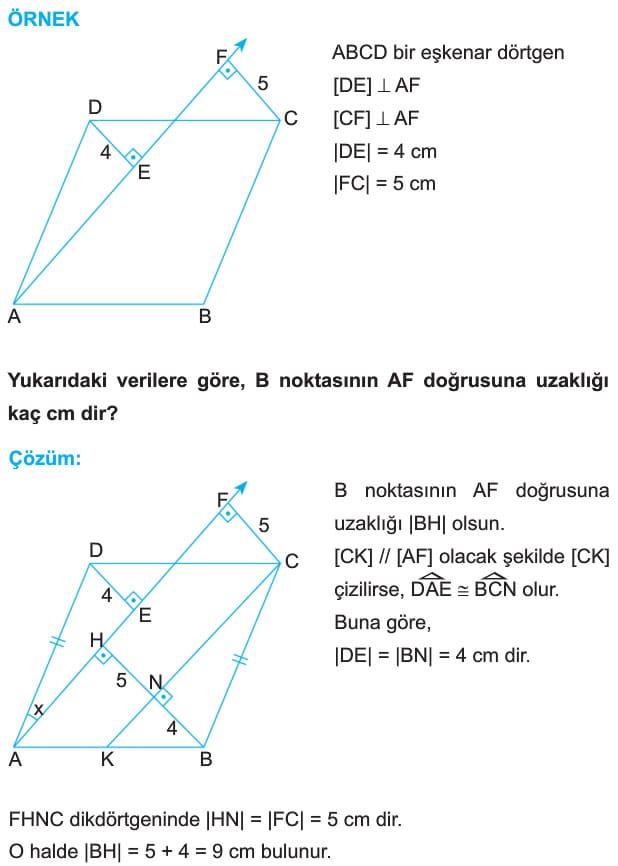
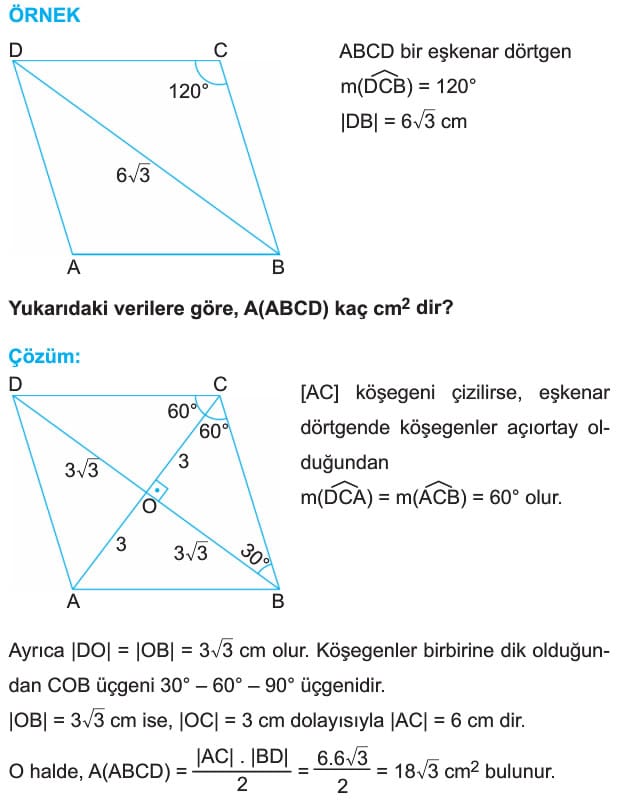
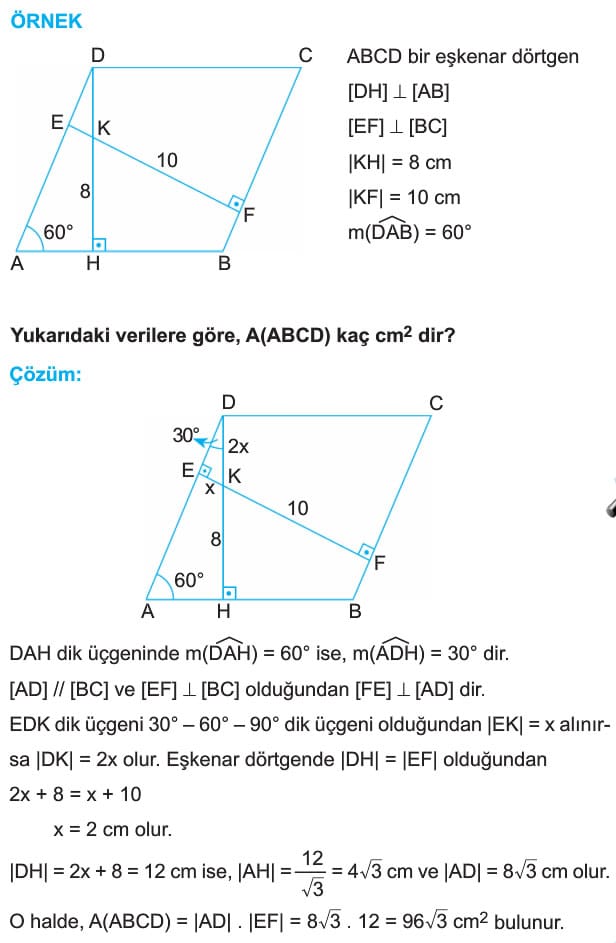
ÖRNEK: ABCD bir eşkenar dörtgen
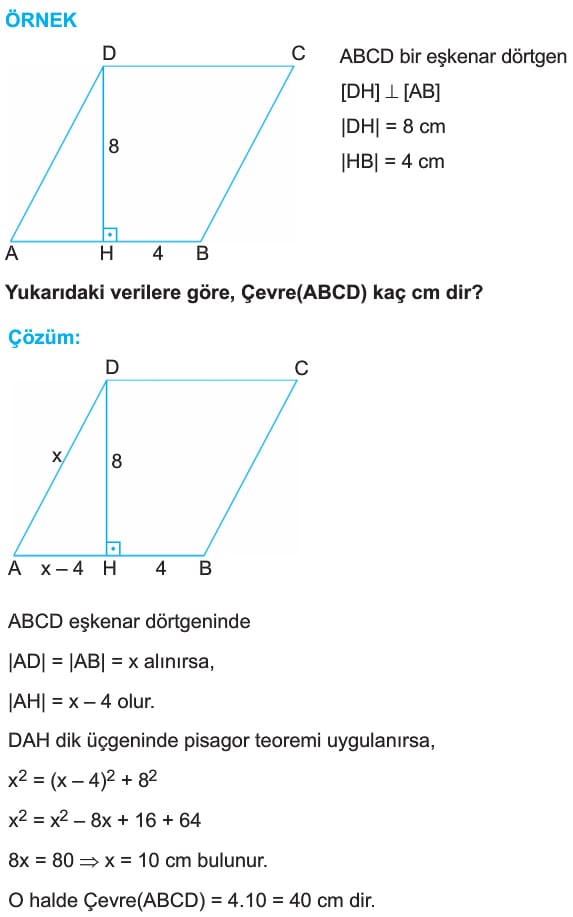
[DH] dik [AB]
[EF] dik [BC]
|KH| = 8 cm
|KF| = 10 cm
m(DAB) = 50°
Yukarıdaki verilere göre, A(ABCD) kaç cm² dir?
Çözüm: DAH dik üçgeninde m(DAH) = 60° ise, m(ADH) = 30° dir.
[AD] // [BC] ve [EF] dik [BC] olduğundan [FE] dik [AD] dir.
EDK dik üçgeni 30° – 60° – 90° dik üçgeni olduğundan [EK] = x alınırsa |DK| = 2x olur. Eşkenar dörtgende |DH| = |EF| olduğundan
2x + 8 = x + 10, x = 2 cm olur.
|DH| = 2x + a = 12 cm ise, |AH| = 12 / √3 = 4√3 cm ve |AD| = 8√3 cm olur.
O halde, A(ABCD) = |AD| . [EF] = 8√3 . 12 = 96√3 cm² bulunur.

Eşkenar dörtgen konusu 11. sınıf geometri dersi müfredatında yer almakta olup ygs, lys ve kpss matematik sınavlarında soru çıkabilmektedir. Eşkenar dörtgen konu anlatımı videosu konu başlıkları,

Eşkenar dörtgen nedir, tanımı.
Eşkenar dörtgende alan bağıntıları
Eşkenar dörtgenin kenar uzunlukları, açı ölçüleri ve köşegenleri ile ilgili genel özellikleri
Eşkenar dörtgen ile ilgili örnek soru çözümleri

Çözümlü Örnek Test Soruları

Konu: Eşkenar Dörtgenin Özellikleri ve Alanı

1. Aşağıdakilerden hangisi eşkenar dörtgenin temel özelliklerinden biri değildir?

A) Tüm kenar uzunlukları eşittir.
B) Karşılıklı açıları birbirine eşittir.
C) Köşegenleri birbirine dik kesişir.
D) Köşegenleri birbirini eşit iki parçaya ayırır.
E) İç açılarının toplamı 360° değil, 180°’dir.

Cevap: E
Çözüm: Eşkenar dörtgenin tüm iç açılarının toplamı 360°’dir, çünkü bir dörtgendir. 180° olması yanlıştır. Doğru cevap E şıkkıdır.

2. Bir eşkenar dörtgenin köşegen uzunlukları 12 cm ve 16 cm’dir. Bu eşkenar dörtgenin alanı kaç cm²’dir?

A) 48
B) 64
C) 72
D) 96
E) 120

Cevap: D
Çözüm: Eşkenar dörtgenin alanı köşegen uzunluklarıyla şu formülden hesaplanır:

$\frac{d_1 \times d_2}{2}$

Burada d₁ = 12 cm ve d₂ = 16 cm olduğundan:

$\frac{12 \times 16}{2} = \frac{192}{2} = 96 \text{ cm²}$

Doğru cevap D şıkkıdır.

3. Bir eşkenar dörtgenin bir iç açısı 60° ise, diğer iç açılarının ölçüleri aşağıdakilerden hangisidir?

A) 30° ve 120°
B) 60° ve 120°
C) 90° ve 90°
D) 45° ve 135°
E) 75° ve 105°

Cevap: B
Çözüm: Eşkenar dörtgende karşılıklı açılar eşittir ve bitişik açılar toplamı 180°’dir.

Verilen açı 60° olduğuna göre, karşısındaki açı da 60°’dir.
Bitişik açılar 180° – 60° = 120° olur.

Bu nedenle açılar 60° ve 120°’dir. Doğru cevap B şıkkıdır.

4. Bir eşkenar dörtgenin çevresi 40 cm ve bir kenar uzunluğu kaç cm’dir?

A) 5
B) 8
C) 10
D) 12
E) 16

Cevap: C
Çözüm: Eşkenar dörtgende tüm kenarlar eşittir. Eğer çevresi 40 cm ise ve dört kenar eşitse:

$cm\text{Bir kenar} = \frac{\text{Çevre}}{4} = \frac{40}{4} = 10 \text{ cm}$

Doğru cevap C şıkkıdır.

5. Eşkenar dörtgenin köşegenleri ile ilgili aşağıdaki ifadelerden hangisi doğrudur?

A) Köşegenler birbirine eşittir.
B) Köşegenler hem açıortay hem de kenarortaydır.
C) Köşegenler dik kesişir ama birbirini eşit iki parçaya ayırmaz.
D) Köşegenler dik kesişir ve birbirini eşit iki parçaya ayırır.
E) Köşegenler yalnızca eşit uzunluktaysa dik kesişir.

Cevap: D
Çözüm: Eşkenar dörtgende köşegenler dik kesişir ve birbirini eşit iki parçaya böler. Ancak eşkenar dörtgende köşegenler eşit uzunlukta değildir (sadece karede eşittir).

Bu yüzden doğru cevap D şıkkıdır.