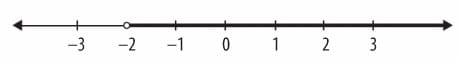Eşitsizlikler 8. Sınıf
EŞİTSİZLİKLER
>, ≥, <, ≤ sembolleri ile yazılan ifadelere eşitsizlik denir. > işaretine büyük, < işaretine küçük, ≥ işaretine büyük veya eşit, ≤ işaretine küçük veya eşit denir. İçinde birinci dereceden bir bilinmeyen bulunan eşitsizliklere birinci dereceden bir bilinmeyenli eşitsizlikler denir.
Dikkat:
ax + b ≥ c, ax + b > c
ax + b ≤ c, ax + b < c
şeklindeki eşitsizlikler birinci dereceden bir bilinmeyenli eşitsizliklerdir.
Örnek Soru: Aşağıdaki ifadelere uygun doğrusal eşitsizlikleri yazalım.
A) Murat’ın yaşı 20’den küçüktür.
B) Çiğdem’in matematik yazılısı notu 80’den fazladır.
C) Araç kullanma yaşı en az 18’dir.
Çözüm:
A) Değişkeni x ile gösterirsek ifadeye uygun matematik cümlesi x < 20 olur. x < 20, “x, 20’den küçüktür.” diye okunur.
B) Değişkeni x ile gösterirsek ifadeye uygun matematik cümlesi, x > 80 olur. x > 80, “x, 80’den büyüktür.” diye okunur.
C) Değişkeni, x ile gösterirsek ifadeye uygun matematik cümlesi x ≥ 18 olur. x ≥ 18 “x, 18’den büyük veya 18’e eşittir.” diye okunur
Örnek Soru: Aşağıdaki ifadelere uygun eşitsizlikleri yazalım.
A) Bir sayının 4 fazlası 16’dan küçüktür.
B) Bir sayının 7 eksiği 14’ten küçük veya 14’e eşittir.
C) Cemil’in yaşının 2 katının 4 yaş fazlası 32’den küçüktür.
Çözüm: Tüm değişkenleri x kabul edelim.
A) x + 4 < 16
B) x – 7 ≤ 14
C) 2x + 4 < 32
A. EŞİTSİZLİKLERİN SAYI DOĞRUSUNDA GÖSTERİMİ
B. BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLERİN ÇÖZÜMÜ
Önemli Bilgi: Bir eşitsizliğin her iki tarafına aynı sayı eklenirse veya çıkarılırsa eşitsizliğin yönü değişmez.
Önemli Bilgi:
- Bir eşitsizliğin her iki tarafı aynı pozitif sayı ile çarpılırsa eşitsizliğin yönü değişmez.
- Bir eşitsizliğin her iki tarafı aynı negatif sayı ile çarpılırsa eşitsizliğin yönü değişir.
- Bir eşitsizliğin her iki tarafı aynı pozitif sayı ile bölünürse eşitsizliğin yönü değişmez.
- Bir eşitsizliğin her iki tarafı aynı negatif sayı ile bölünürse eşitsizlik yön değiştirir.
8. Sınıf Eşitsizlikler Konu anlatımı Lgs Ders Notları Çözümlü Sorular Özet
İki büyüklük arasında karşılaştırma yapılırken dengede olma durumu eşitlik ile, dengede olmama durumu eşitsizlik ile ifade edilir. İki büyüklük arasında yapılan karşılaştırmada = (Eşittir), > (Büyüktür.) < (Küçüktür), ≥ (Büyük veya eşittir.) ve ≤ (Küçük veya eşittir.) sembollerinden biri kullanılır.
Terazinin her iki kefesinden 1 kg'lık kütleler çıkarıldığında bu durumu gösteren matematik cümle 2 < 5 şeklindedir. Terazinin sol kefesindeki kütlelerin daha büyük olması için bu kefeye konması gereken kütle miktarını bilinmeyen kabul ederek bu durumu gösteren matematik cümle 3 + x > 6 şeklinde yazılabilir.
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLER
Aşağıdaki eşitsizlikleri inceleyelim.
- x'in 5 fazlası 12'den küçüktür.
x + 5 < 12 - x'in 3 fazlası 8'e eşit veya 8'den küçüktür.
x+3 ≤ 8 - x'in 7 eksiği 16'dan büyüktür.
x - 7 > 16 - x'in 6 fazlası 20'ye eşit veya 20'den büyüktür.
x + 6 ≥ 20
BİR BİLİNMEYENLİ EŞİTSİZLİKLERİ SAYI DOĞRUSUNDA GÖSTERME
x > - 2 ve x ≤ 1 eşitsizliklerini sayı doğrusunda gösterelim.
x > - 2 eşitsizliği, -2'den büyük sayılara karşılık gelmektedir. -2 sayısı bu sayılara dâhil olmadığından, -2 sayısının bulunduğu noktanın içi boş alınır.
x ≤ 1 eşitsizliği, 1 veya 1'den küçük sayılara karşılık gelmektedir. 1 sayısı bu sayılara dâhil olduğundan, 1 sayısının bulunduğu noktanın içi dolu alınır.
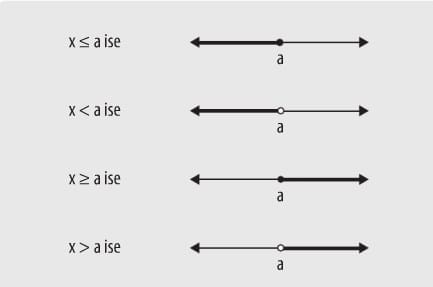
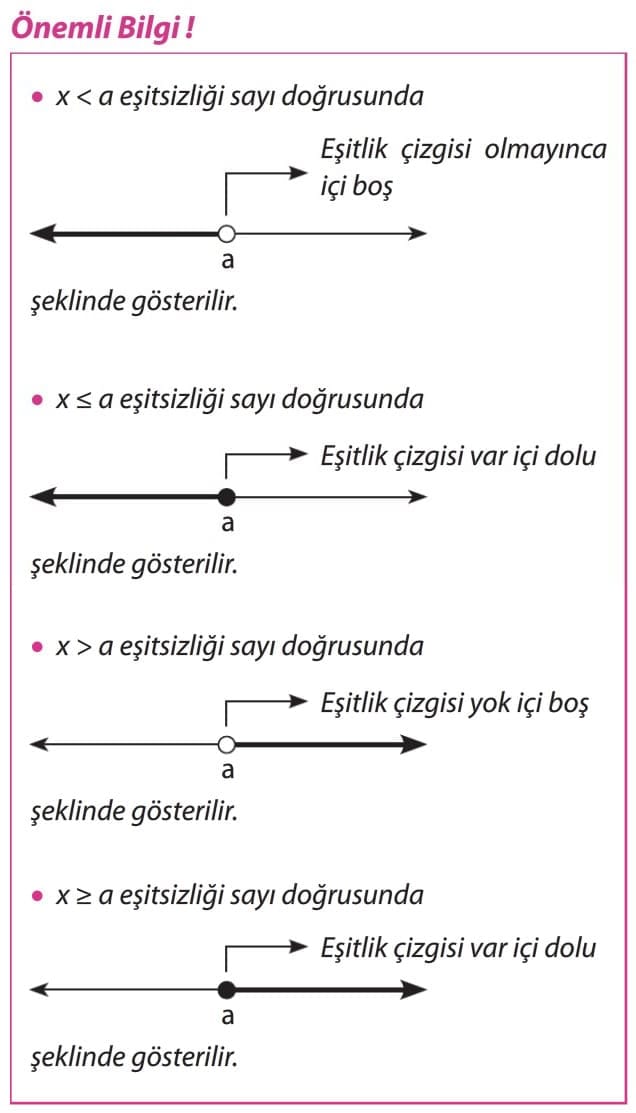
a bir sayı, x bilinmeyen olsun. Eşitsizliklerin çözüm kümesi sayı doğrusu üzerinde aşağıdaki gibi gösterilir.
- < ve > sembollerinde sayının kendisi çözüme dâhil olmadığından sayının bulunduğu noktanın içi boş alınır.
- ≥ ve ≤ sembollerinde sayının kendisi çözüme dâhil olduğundan sayının bulunduğu noktanın içi dolu alınır.
BİR BİLİNMEYENLİ EŞİTSİZLİKLERİN ÇÖZÜMÜ
"3 fazlası 8 veya 8'den küçük olan sayılar" ifadesine uygun eşitsizliği yazarak çözümünü bulalım ve bu çözümü sayı doğrusunda gösterelim.
Sayılar x ile temsil edildiğinde, verilen ifadeye uygun eşitsizlik; x + 3 ≤ 8 şeklinde yazılır.
Bu eşitsizliği çözelim
x+3 ≤ 8
x+3-3 ≤ 8-3
x ≤ 5
Eşitsizliğin çözümünü 5 veya 5'ten küçük sayılar oluşturur. x ≤ 5 eşitsizliğini sağlayan sayılar sayı doğrusunda aşağıdaki gibi gösterilir.
Önemli: Bir eşitsizliğin her iki tarafına aynı sayı eklenir veya her iki tarafından aynı sayı çıkarılırsa eşitsizlik bozulmaz. Bir eşitsizliğin her iki tarafı pozitif bir sayı ile çarpılır veya bölünürse eşitsizlik bozulmaz. Bir eşitsizliğin her iki tarafı negatif bir sayı ile çarpılır veya bölünürse eşitsizlik yön değiştirir.
Bir eşitsizliği çözmek, değişkenin o eşitsizliği bozmayan değerlerini bulmaktır. Eşitsizlik çözümünde birden fazla değer bulunabilir.
Örnek: Ahu'nun cebindeki para Serap'ın cebindeki paranın 5 katının 10 TL eksiğinden fazladır. Serap'ın cebinde 27 TL olduğuna göre Ahu'nun cebindeki para için ne söylenebilir?
Ahu'nun cebindeki parayı yTL, Serap'ın cebindeki parayı xTL ile temsil edelim. Buna göre y > 5x - 10 eşitsizliği yazılabilir. Serap'ın cebinde 27 TL olduğuna göre eşitsizlikte x yerine 27 yazarsak eşitsizliği
çözelim.
y > 5x - 10
y > 5.27 - 10
y > 135 - 10
y > 125
Ahu'nun cebindeki para için 125 TI.'den fazla olduğu söylenebilir.
Örnek: Ayşe biriktiıdiği parasından beş hafta üst üste 650 TL'lik alışveriş yapmıştır. Bu durumda Ayşe'nin geriye en az 4300 TL'si kaldığımı göre, biriktirdiği para en az kaç TL'dir?
Ayşe'nin biriktirdiği para x TL olsun. Ayşe beş hafta üst üste 650 TL harcadığına göre, toplam harcanan para; 5 . 650 = 3250 TL'dir. Bu harcamadan sonra Ayşe'nin geriye en az 4300 TL'si kaldığına göre, bunu eşitsizlik kullanarak aşağıdaki gibi ifade edebiliriz.
x - 3250 ≥ 4300
Bu eşitsizliği çözelim.
x - 3250 ≥ 4300
x ≥ 4300 + 3250
x ≥ 7550
Buna göre Ayşe'nin biriktirdiği para en az 7550 TL'd
Örnek Soru: 10 > -5 eşitsizliğinin her iki tarafına 2 sayısını ekleyip eşitsizliğin yönünün değişip değişmediğini inceleyelim.
Çözüm: 10 > -5 ise 10 + 2 > -5 + 2 ise 12 > -3 olur. Eşitsizliğin yönü değişmedi.
Örnek Soru: 10 > -5 eşitsizliğinin her iki tarafından 4 sayısını çıkaralım. Eşitsizliğin yönünün değişip değişmediğini inceleyelim.
Çözüm: 10 > -5 ise 10-4 > -5 -4 6 > -9 olur. Eşitsizliğin yönü değişmedi.