Düzlemde Öteleme Dönüşümü 12. Sınıf
Öteleme: Bir şeklin boyutları bozulmadan yer değiştirmesine öteleme dönüşüm hareketi denir. Ötelemede biçim, boyut ve yön değişmez. Öteleme dönüşüm hareketi yapılırken x ve y eksenleri boyunca belirtilen yönde, belirtilen birim kadar nokta ötelenir. Sağa ve sola öteleme dönüşümü hareketi x eksenine paralel olarak, yukarı ve aşağı öteleme dönüşüm hareketi ise y eksenine paralel olarak yapılır.
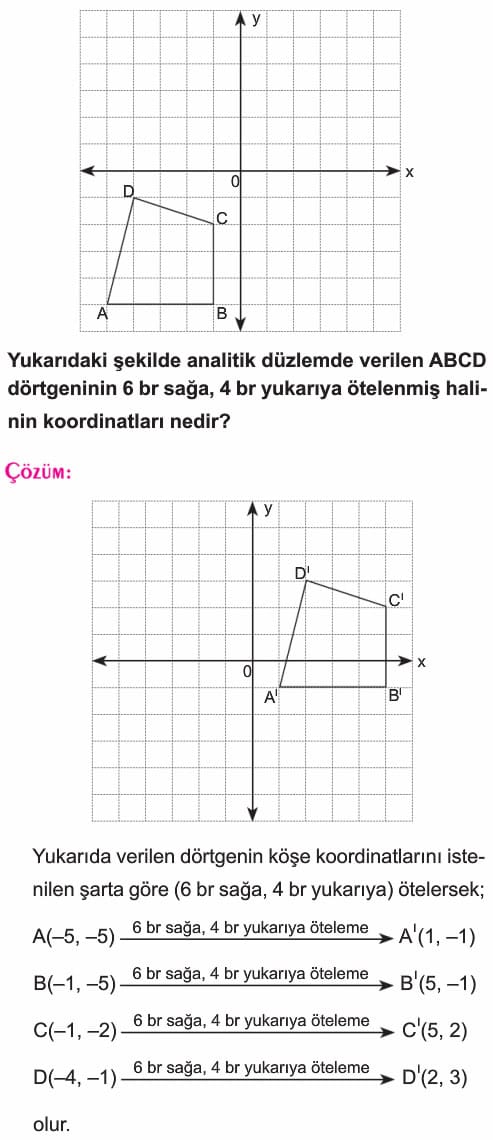
Düzlemde Öteleme Dönüşümü Soruları ve Çözümleri
Analitik Düzlemde Temel Dönüşümler konu anlatımı soruları çözümleri 12. Sınıf Ayt Matematik
Örnek: Analitik düzlemde A(3, 5) noktası 4 br sağa ve 3 br aşağıya öteleniyor. A noktasının bu öteleme dönüşümü altındaki görüntüsünün koordinatları kaçtır?
Çözüm: A noktasının öteleme dönüşümü sonrasında görüntüsü A' olsun. A noktasının 4 br sağa ve 3 br aşağıya ötelenmesiyle A'(7, 2) noktası elde edilir.
Soru: A(x, y) noktası analitik düzlemde 3 br sola ve 5 br aşağı öteleniyor. A noktasının bu öteleme dönüşümü altındaki görüntüsünün koordinatları A'(4, -2) olduğuna göre, x + y toplamı kaçtır?
A) 6 B) 7 C) 8 D) 9 E) 10
Soru: A(a, b) noktası analitik düzlemde 2 br sağa ve 6 br yukarıya öteleniyor. A noktasının bu öteleme dönüşümü altındaki görüntüsünün koordinatları A'(3, —2) olduğuna göre, b — a farkı kaçtır?
A) —7 B) —8 C) —9 D) —10 E) —11
Soru: Analitik düzlemde A(2, 6) noktası 4 br sağa ve 2 br yukarı öteleniyor. A noktasının bu öteleme dönüşümü altındaki görüntüsünün koordinatları aşağıdakilerden hangisidir?
A) (6, 5) B) (6, 6) C) (6, 8) D) (8, 6) E) (6, 4)
Soru: Analitik düzlemde A(-4, —3) noktası 2 br sola ve 4 br aşağı öteleniyor. A noktasının bu öteleme dönüşümü altındaki görüntüsünün koordinatları aşağıdakilerden hangisidir?
A) (-6, —7) B) (-6, 6) C) (-2, 1)
D) (-6, 7) E) (-6, 1)
Soru: 3x — 5y + 1 = 0 doğrusu x ekseni doğrultusunda 2 br sola, y ekseni doğrultusunda 4 br yukarı ötelendiğinde oluşan doğrunun denklemi nedir?
A) 3x — 5y + 27 = 0
C) 3x — 5y — 27 = 0
B) 3x + 5y + 24 = 0
D) 3x + 5y + 27 = 0
E) 3x + 5y — 32 = 0