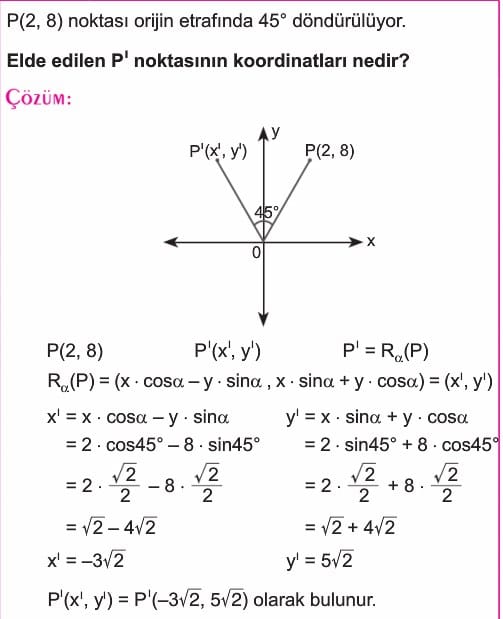
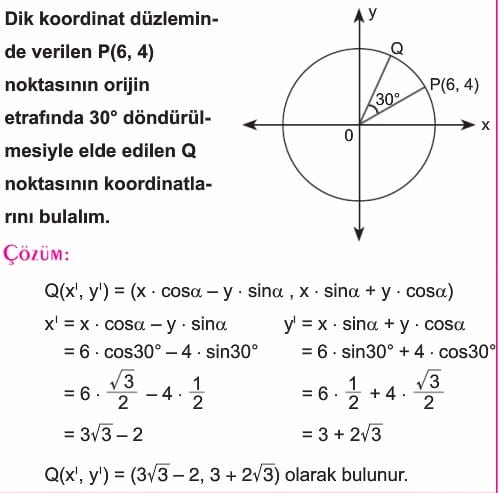
Düzlemde P(x, y) noktalarının orijin etrafında α açısı kadar döndürülmesi ile elde edilen nokta Q(x’, y’) ise
Q = R_α(P) = (x.cosα – y.sinα, x.sinα + y.cosα) dır. Burada R_α ya dönme dönüşümü denir. (R_α(P), bir P noktasının α açısı kadar orijin etrafında döndürülmesini simgeler.)

Düzlemin her P noktası için R_α(P) dönmesi yapılabileceğinden
R_α: R² → R² şeklinde bir dönüşümdür.

• Dönme yalnızca bir noktayı değiştirmez diğer bütün noktaları değiştirir. Değişmeyen noktaya dönme merkezi denir.
• Bir dönme dönüşümünde α açısı kadar döndürelim dendiğinde, döndürme yönü pozitif yani saat yönünün tersinedir. -α açısı kadar döndürme ise negatif yönde yani saat yönünde α açısı kadar döndürmedir.
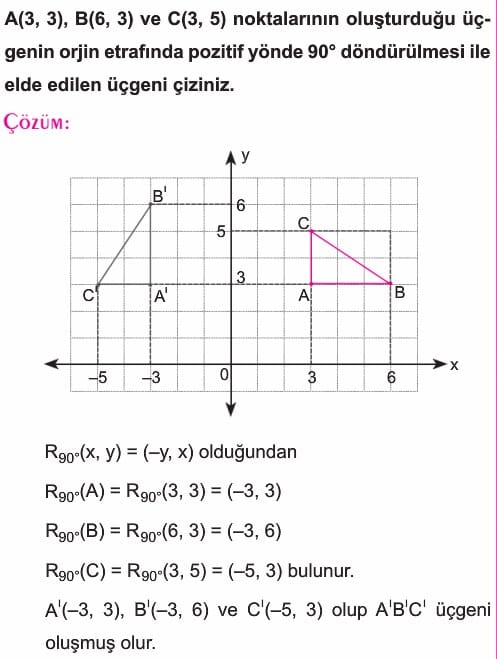
• Bir P(x, y) noktasının orijin etrafında pozitif yönde 90° döndürülmesiyle elde edilen noktanın koordinatları Q(-y, x) dir.
  R_90° (x, y) = (-y, x) olur.
• Bir P(x, y) noktasının orijin etrafında negatif yönde 90° (veya pozitif yönde 270°) dönmesiyle elde edilen noktanın koordinatları Q(y, -x) dir.
  R^-1_90° (x, y) = (y, -x) olur.
• Bir P(x, y) noktasının orijin etrafında negatif yönde 180° dönmesiyle elde edilen noktanın koordinatları Q(-x, -y) dir.
  R_180° (x, y) = (-x, -y) dir.

Düzlemde Dönme Dönüşümü Soruları ve Çözümleri

Çözümlü Örnek Test Soruları

Düzlemde Dönme Dönüşümü

1. Koordinat düzleminde, orijin etrafında saat yönünde 90° döndürülen bir noktanın (x, y) koordinatları ne olur?
A) (-y, x)
B) (y, -x)
C) (-x, -y)
D) (x, y)
Çözüm: Saat yönünde 90° döndürüldüğünde, bir noktanın koordinatları (x, y) iken (y, -x) olur. Doğru cevap B’dir.

2. Orijin etrafında saat yönünün tersine 180° döndürülen bir noktanın (3, -4) yeni koordinatları nedir?
A) (3, -4)
B) (-3, 4)
C) (-3, -4)
D) (4, -3)
Çözüm: Saat yönünün tersine 180° döndürme, noktayı (-x, -y) haline getirir. Bu durumda, (3, -4) noktası (-3, 4) olur. Doğru cevap B’dir.

3. Orijin etrafında 270° saat yönünde döndürülen (5, 2) noktasının yeni koordinatları nedir?
A) (-2, 5)
B) (2, -5)
C) (-5, -2)
D) (5, 2)
Çözüm: Saat yönünde 270° döndürmek, saat yönünün tersine 90° döndürmekle aynıdır. Bu durumda, (x, y) noktası (-y, x) olur. (5, 2) noktası (-2, 5) olur. Doğru cevap A’dır.

4. Orijin etrafında saat yönünün tersine 60° döndürülen bir noktanın dönüşüm matrisini aşağıdakilerden hangisi ifade eder?
A) [0 -1; 1 0]
B) [cos 60° -sin 60°; sin 60° cos 60°]
C) [cos 60° sin 60°; -sin 60° cos 60°]
D) [1 0; 0 1]
Çözüm: Saat yönünün tersine θ derece döndürme matrisinin genel formülü: [cos θ -sin θ; sin θ cos θ]. Bu durumda, θ = 60° yerine konursa doğru cevap B olur.

5. (2, -3) noktası, orijin etrafında saat yönünün tersine 90° döndürülürse yeni koordinatları ne olur?
A) (3, 2)
B) (-3, 2)
C) (2, -3)
D) (-2, -3)
Çözüm: Saat yönünün tersine 90° döndürme formülü: (x, y) → (-y, x). Bu durumda, (2, -3) noktası (3, 2) olur. Doğru cevap A’dır.

6. Bir (x, y) noktasının orijin etrafında döndürülmesi ile elde edilen yeni koordinatlar aşağıdaki dönüşüm matrislerinden hangisi ile ifade edilebilir?
A) [0 1; -1 0]
B) [cos θ -sin θ; sin θ cos θ]
C) [1 0; 0 -1]
D) [-1 0; 0 -1]
Çözüm: Genel döndürme matrisi, orijine göre θ derece döndürme için [cos θ -sin θ; sin θ cos θ]. Doğru cevap B’dir.