• Terimler: Dış bükey dörtgen, iç bükey dörtgen, köşegen, alan, çevre.
• Sembol ve Gösterimler: A(ABCD), Çevre(ABCD).
• Yol Haritası: Bu bölüm için tavsiye edilen süre 6 ders saatidir.

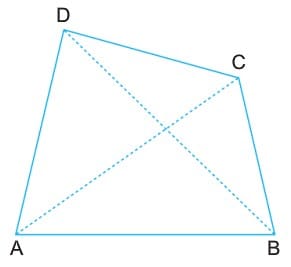
Tanım: Herhangi üçü doğrusal olmayan A, B, C, D noktalarını birleştiren [AB], [BC], [CD] ve [DA] doğru parçalarının birleşiminden oluşan kapalı şekle dörtgen denir.

Şekildeki A, B, C, D noktalarına dörtgenin köşeleri, [AB], [BC], [CD] ve [DA] doğru parçalarına dörtgenin kenarları denir. Birer köşesi ortak olan kenarlara komşu kenarlar, ortak köşesi olmayan kenarlara ise karşı kenarlar denir. [AC] ve [BD] doğru parçalarına dörtgenin köşegenleri denir.

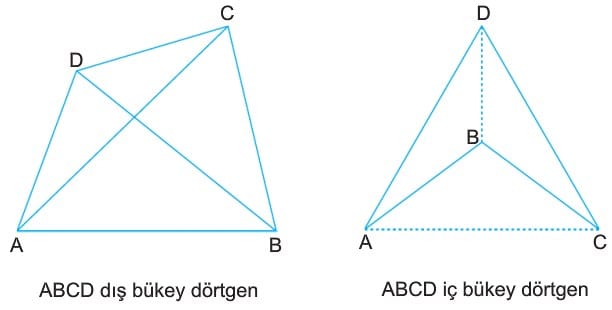
Dış bükey dörtgenlerin köşegenlerinin her ikisi de dörtgenin içindedir. Oysa, iç bükey dörtgenlerde köşegenlerden biri dörtgenin içinde, diğeri dörtgenin dışındadır.

Dörtgende Açı Özellikleri

1. 

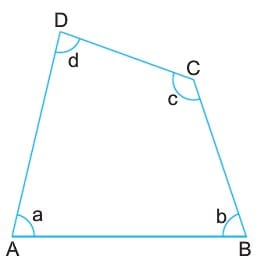
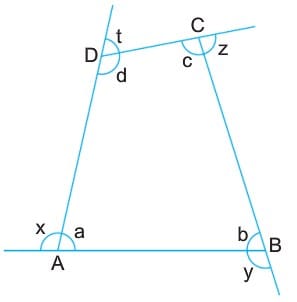
Dörtgenlerin iç açılarının ölçüleri toplamı 360⁰ dir.
a + b + c + d = 360°

2.

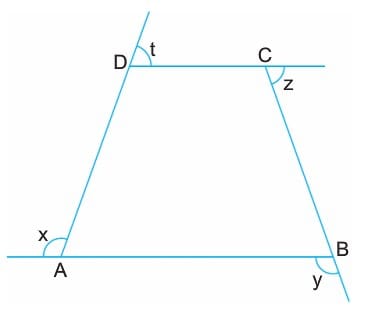
Dörtgenlerin dış açılarının toplamı da 360° dir.
x + y + z + t = 360°

3.

a, b, c, d iç açılar ve x, y, z, t dış açılar olmak üzere,
a + c = y + t
b + d = x + z dir.

4. 

Dörtgenlerde Uzunluk

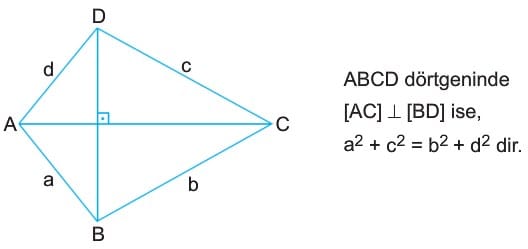
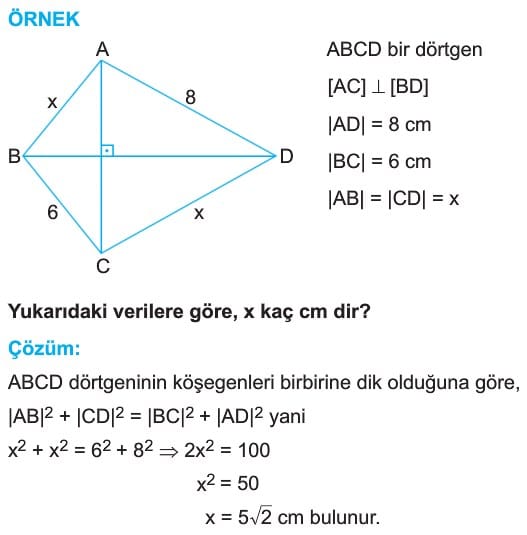
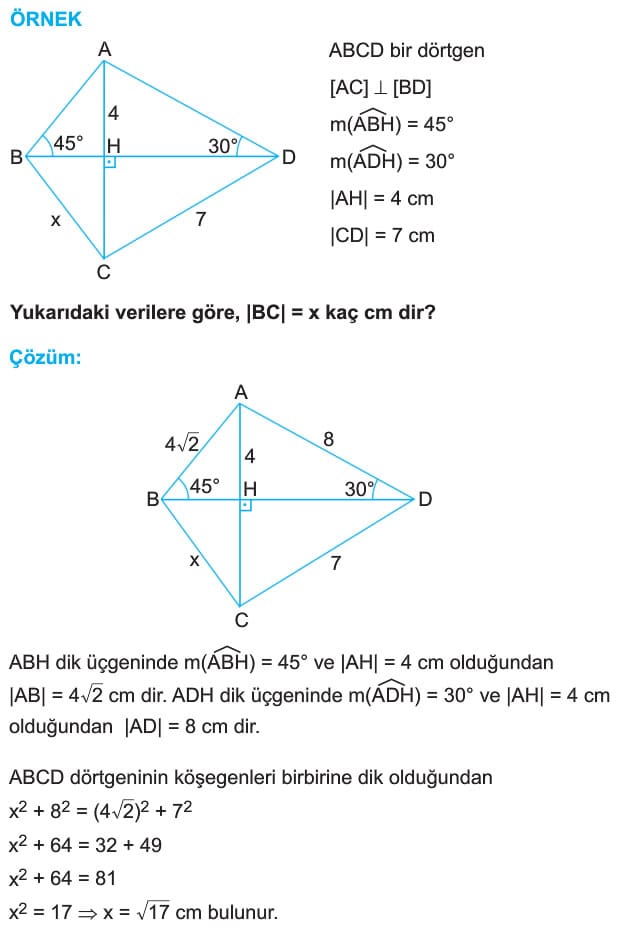
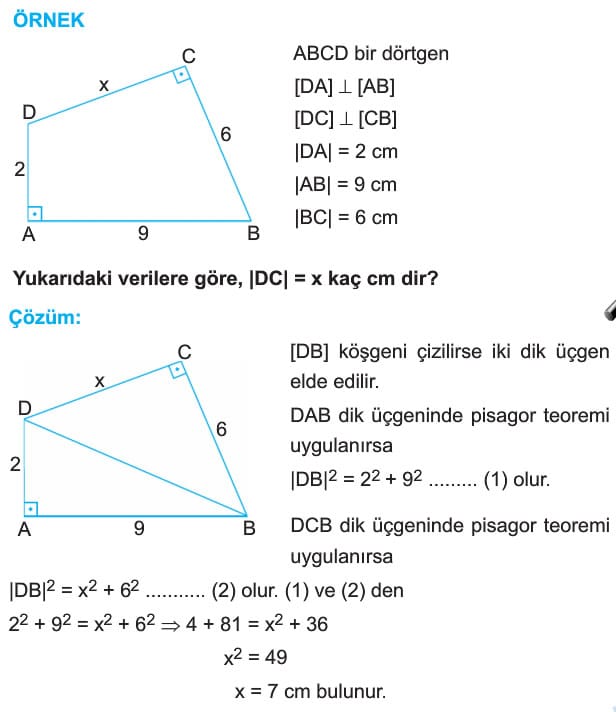
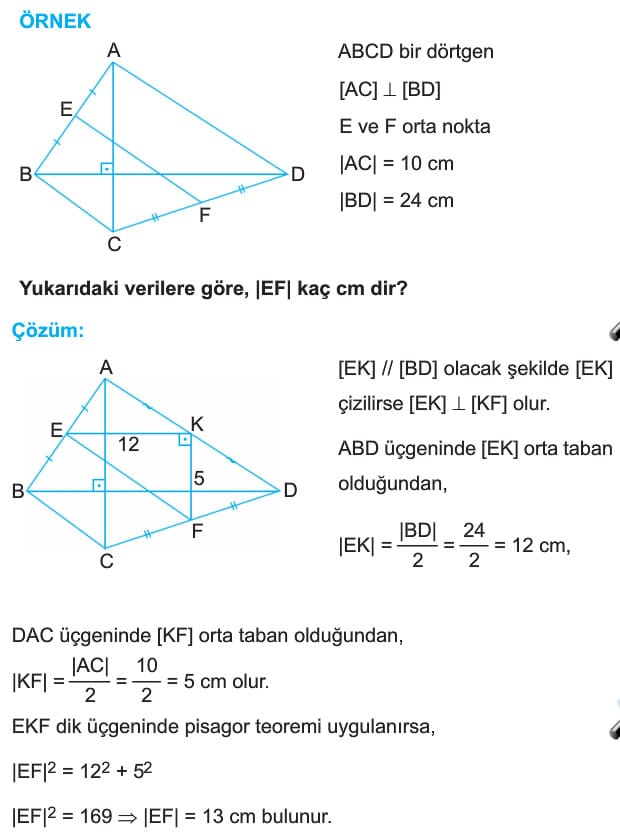
Bir dörtgenin köşegenleri birbirine dik ise, karşılıklı kenarlarının uzunluklarının kareleri toplamı birbirine eşittir.

Çözümlü Örnek Test Soruları

Soru 1:
Bir dörtgenin iç açılarının ölçüleri toplamı kaç derecedir?

a) 180°
b) 270°
c) 360°
d) 540°
e) 720°

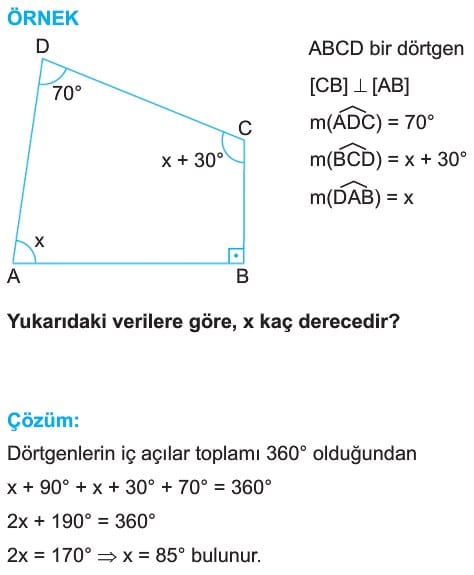
Çözüm:
Bir dörtgenin iç açılarının toplamı (n-2) x 180° formülü ile bulunur. Dörtgen için n = 4 olduğundan,
(4-2) x 180° = 2 x 180° = 360°
Cevap: c) 360°

---

Soru 2:
Bir dikdörtgenin uzun kenarının uzunluğu 10 cm, kısa kenarının uzunluğu 6 cm’dir. Bu dikdörtgenin çevresi kaç cm’dir?

a) 16 cm
b) 26 cm
c) 32 cm
d) 36 cm
e) 40 cm

Çözüm:
Dikdörtgenin çevresi 2 x (uzun kenar + kısa kenar) formülü ile bulunur.
2 x (10 + 6) = 2 x 16 = 32 cm
Cevap: c) 32 cm

---

Soru 3:
Bir karede bir kenar uzunluğu 8 cm ise, bu karenin alanı kaç cm²’dir?

a) 16 cm²
b) 32 cm²
c) 48 cm²
d) 64 cm²
e) 80 cm²

Çözüm:
Karenin alanı, bir kenar uzunluğunun karesi ile bulunur.
8 x 8 = 64 cm²
Cevap: d) 64 cm²

---

Soru 4:
Bir yamukta üst taban 12 cm, alt taban 18 cm ve yükseklik 5 cm olarak verilmiştir. Bu yamuğun alanı kaç cm²’dir?

a) 60 cm²
b) 75 cm²
c) 90 cm²
d) 100 cm²
e) 125 cm²

Çözüm:
Yamuğun alanı, (üst taban + alt taban) x yükseklik / 2 formülü ile bulunur.
(12 + 18) x 5 / 2 = 30 x 5 / 2 = 150 / 2 = 75 cm²
Cevap: b) 75 cm²

---

Soru 5:
Bir paralelkenarın tabanı 9 cm, yüksekliği 7 cm’dir. Bu paralelkenarın alanı kaç cm²’dir?

a) 42 cm²
b) 49 cm²
c) 54 cm²
d) 63 cm²
e) 72 cm²

Çözüm:
Paralelkenarın alanı taban x yükseklik ile bulunur.
9 x 7 = 63 cm²
Cevap: d) 63 cm²

Dörtgenler Tonguç Akademi

Dörtgenler Hocalara Geldik

Dörtgenler Şenol Hoca

Dörtgenler Ekol Hoca

Dörtgenler konusu 11. sınıf geometri dersi müfredatında yer almaktadır ve ygs, lys ile kpss matematik sınavlarında soru çıkmaktadır.

Geometri dersi Dörtgenler konu anlatımı videosu konu başlıkları,

• Dörtgenlerin genel özellikleri
• Dörtgenlerde kenar, açı ve köşegen özellikleri
• Dörtgenlerde alan formülleri

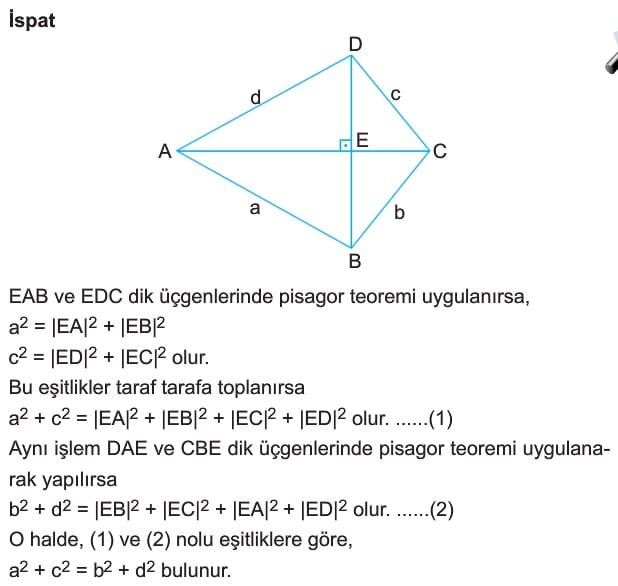
İspat: EAB ve EDC dik üçgenlerinde pisagor teoremi uygulanırsa,
a2 = |EA|2 + |EB|2
c2 = |ED|2 + |EC|2 olur.
Bu eşitlikler taraf tarafa toplanırsa
a2 + c2 = |EA|2 + |EB|2 + |EC|2 + |ED|2 olur. ……(1)
Aynı işlem DAE ve CBE dik üçgenlerinde pisagor teoremi uygulanarak yapılırsa
b2 + d2 = |EB|2 + |EC|2 + |EA|2 + |ED|2 olur. ……(2)
O halde, (1)ve (2) nolu eşitliklere göre,
a2 + c2 = b2 + d2 bulunur.