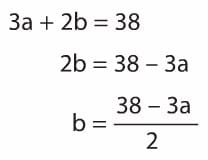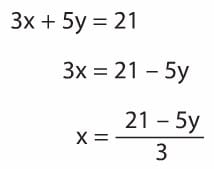Doğrusal Denklemler 8. Sınıf
Doğrusal Denklemler
- 1. Konu: Birinci Dereceden Bir Bilinmeyenli Denklemler
- 2. Konu: Koordinat Sistemi
- 3. Konu: Doğrusal İlişkiler
- 4. Konu: Doğrusal Denklemlerin Grafiği
- 5. Konu: Doğrusal İlişki İçeren Gerçek Hayat Durumları
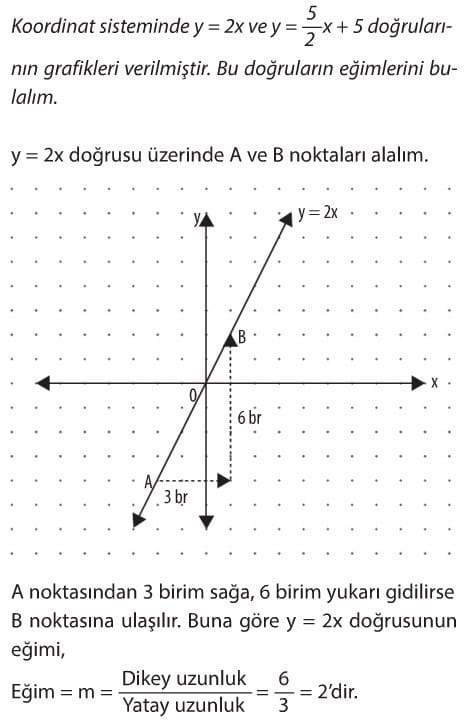
- 6. Konu: Doğrunun Eğimi
x ve y iki değişken olmak üzere ax + by + c = 0 şeklindeki denklemlere doğrusal denklem denir. Bu ifadedeki c sayısına sabit sayı, a, b ve c sayılarına kat sayı adı verilir. a ve b kat sayıları aynı anda 0 (sıfır) değerini alamaz.
DOĞRUSAL İLİŞKİLER
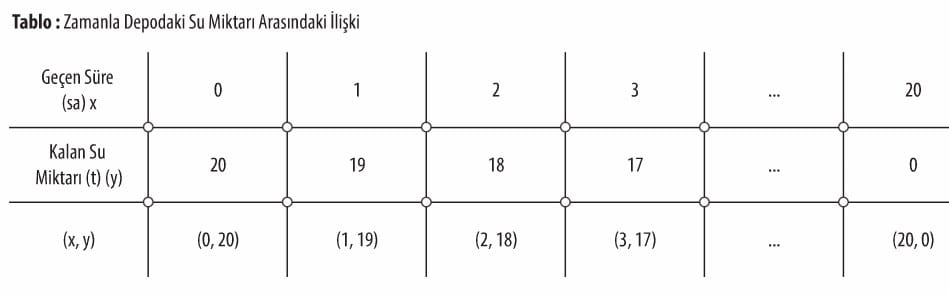
Bir su deposunda 20 ton su vardır. Depodan her l saatte 1 ton su kullanılmaktadır. Geçen süre saat cinsinden x ile, depoda kalan su miktarı ton cinsinden y ile gösterilsin. Geçen süre ile depoda kalan su miktarı arasındaki ilişkiyi inceleyelim.
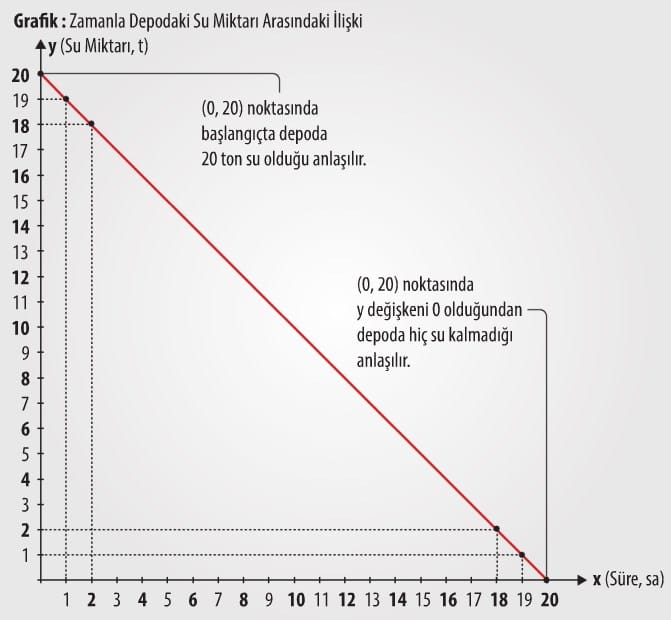
Geçen süre ile depoda kalan su miktarı arasındaki doğrusal ilişkinin denklemi y = 20 – x şeklindedir. Bu ilişkinin grafiği aşağıdaki gibi çizilebilir.
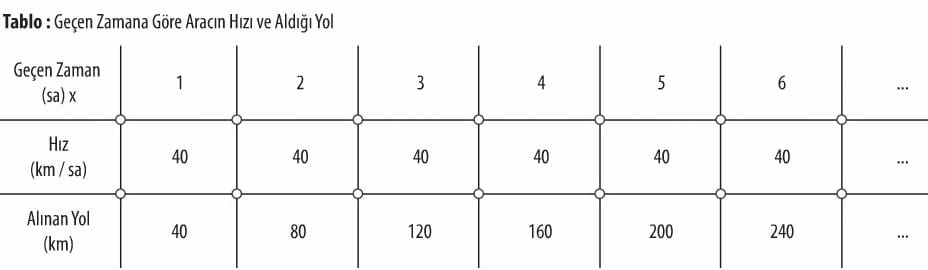
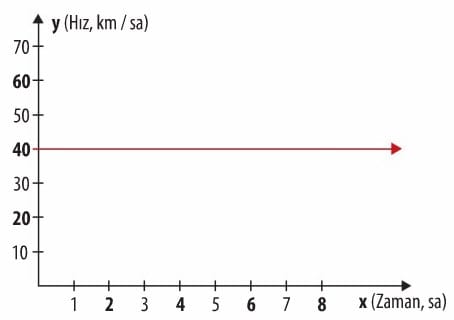
Bir araç her bir saatte 40 km yol alarak gitmektedir. Aşağıdaki tabloyu inceleyelim. Belirlenen x ve y değerlerine göre aralarındaki ilişkinin denklemini yazalım ve grafiğini çizelim.
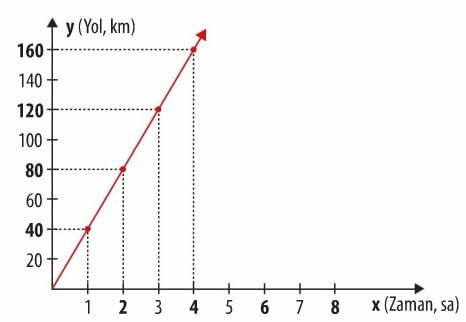
Geçen zaman saat cinsinden x ile, alınan yol miktarı km cinsinden y ile gösterilerek; x ile y arasındaki ilişkinin denklemi y = 40x olarak yazılır. Alınan yol zamana bağlı olarak değişmektedir. x ile y birbirlerine bağlı olarak değişir.
Geçen zaman saat cinsinden x ile, aracın hızı km/sa cinsinden y ile gösterilerek; x ile y arasındaki ilişkinin denklemi y = 40 olarak yazılır. Hız zamana bağlı olarak değişmediğinden y bağımsız değişkendir.
EĞİM
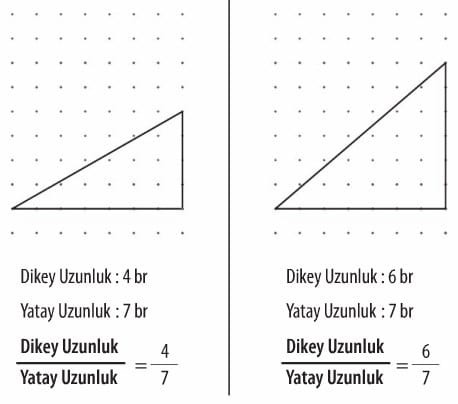
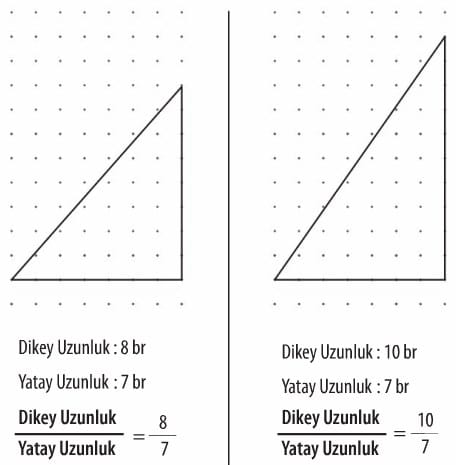
Aşağıda dört farklı üçgen çizilerek, farklı yokuş modelleri verilmiştir. 4. üçgendeki yokuş modeline tırmanmak daha zordur. Bu üçgendeki dikey uzunluğun yatay uzunluğa oranı da diğer üçgenlerdeki oranlardan daha büyüktür.
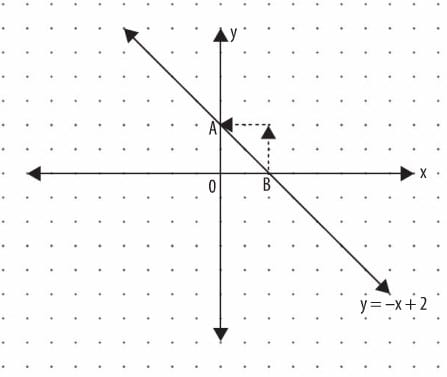
y : -x + 2 doğrusunun grafiğini çizerek eğimini bulalım. Bir doğrunun grafiğini çizebilmek için, bu doğru üzerinde olan iki noktanın koordinatlarının bilinmesi yeterlidir.
x=0 için y=0+2=2’dir.
y=0 için 0=-x+2 x = 2’dir.
Doğru x eksenini (2, 0), y eksenini (0, 2) noktasında keser.
B noktasından 2 birim yukarı, 2 birim sola gidilirse A noktasına ulaşılır. Bu doğru sola yatık olduğundan eğimi negatiftir.
BİR DEĞİŞKENİN DİĞERİ CİNSİNDEN İFADESİ
Bir doğrusal denklemde bir değişkenin diğeri cinsinden ifadesi yazılırken istenen değişken eşitliğin bir tarafında yalnız bırakılır.
x tane kırmızı, y tane yeşil topun bulunduğu bir sepetteki topların sayısı 20’dir. Bu ifadeye karşılık gelen doğrusal denklem x + y = 20’dir. Kırmızı top sayısının (x), yeşil top sayısı (y) cinsinden ifadesi x + y = 20 olduğundan x = 20 – y şeklinde yazılır. Yeşil top sayısının (y), kırmızı top sayısı (x) cinsinden ifadesi x + y = 20 olduğundan y = 20 – x şeklinde yazılır.
Meral kızından 35 yaş büyüktür. Bu ifadeye karşılık gelen doğrusal denklem Meral’in yaşı a, kızının yaşı b ile gösterilerek a – b = 35 şeklinde yazılabilir. Meralin yaşının (a), kızının yaşı (b) cinsinden ifadesi a – b = 35 olduğundan a = 35 + b şeklinde yazılır. Kızının yaşının (b), Meralin yaşı cinsinden ifadesi a – b = 35 olduğundan b = a – 35 şeklinde yazılabilir.
Elmanın kilogramı a TL, portakalın kilogramı b TL’dir. 3 kg elma ile 2 kg portakal alınarak tüm meyvelere 38 TL ödeniyor. Bir kilogram portakalın fiyatını bir kilogram elmanın fiyatı cinsinden yazalım.
İfadeye ait doğrusal denklemi yazalım.
Elmalara ödenen ücret 3a, portakallara ödenen ücret 2b, tüm meyvelere ödenen ücret 3a + 2b şeklinde yazılır. 3a + 2b = 38
Bir kilogram portakalın fiyatı bir kilogram elmanın fiyatı cinsinden (b’yi a cinsinden) yazalım.
3a + 2b = 38 denkleminde b’yi a cinsinden yazmak için denklemde b’yi eşitliğin bir tarafında yanlız bırakalım.
x tane üçgen, y tane beşgenin kenar sayıları toplamı 21’dir. Üçgen sayısının beşgen sayısı cinsinden ifadesini bulalım. İfadeye ait doğrusal denklemi yazalım.
Üçgenlerin toplam kenar sayısı 3x, beşgenlerin toplam kenar sayısı 5y tüm şekillerin kenar sayıları toplamı 21 ise 3x + 5y = 21 yazılır.
x’in y cinsinden ifadesi yazılacağından, denklemde x’i eşitliğin bir tarafında yalnız bırakalım.
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
Araç 99 km yolu 15 litre benzin tüketerek gidebilir. Bir bilinmeyenli rasyonel cebirsel ifadeler içeren eşitliklere bir bilinmeyenli rasyonel denklemler adı verilir. Bir bilinmeyenli rasyonel denklemlerde değişkenin yerine koyulduğunda denklemi sağlayan gerçek sayıya denklemin çözümü adı verilir. Çözümün doğru olup olmadığını kontrol etmek için bulunan değer x’in yerine yazılarak eşitliğin sağlanıp sağlanmadığına bakılır. Eşitlik sağlanıyor ise çözüm doğrudur.
Rasyonel ifadeler içeren denklemler çözülürken paydalar eşitlenerek iki taraf da ortak paydada toplanır. Her iki tarafın paydaları eşit olduğundan payları da eşit olur. Elde edilen bu eşitlikle denklem çözümü yapılır.
Doğrusal Denklemler konu anlatımı 8.sınıf Lgs Çözümlü Sorular
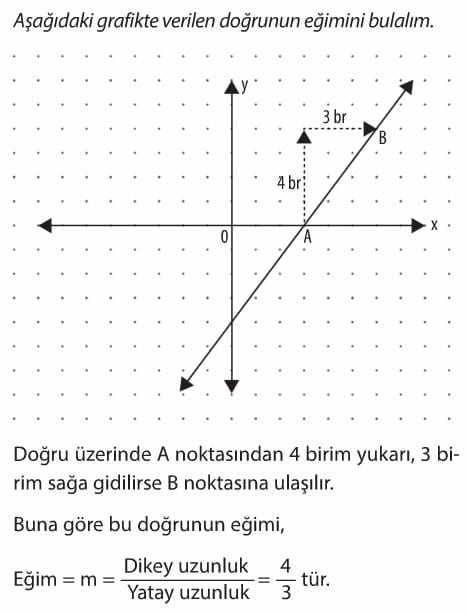
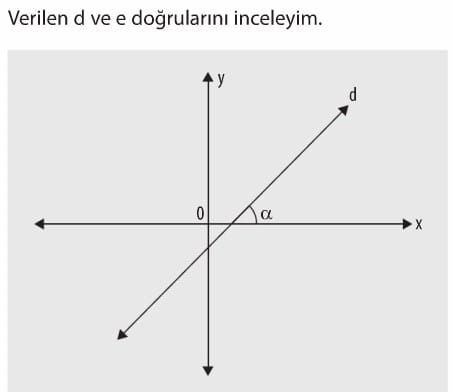
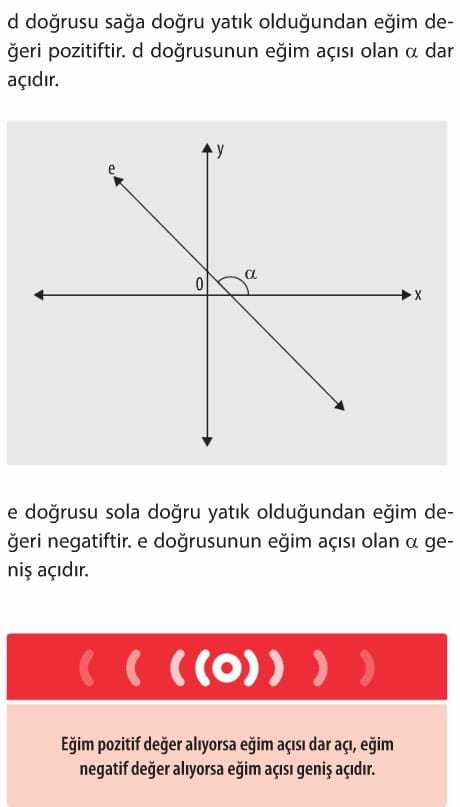
d doğrusu sağa doğru yatık olduğundan eğim değeri pozitiftir. d doğrusunun eğim açısı olan alfa dar açıdır. e doğrusu sola doğru yatık olduğundan eğim değeri negatiftir. e doğrusunun eğim açısı olan alfa geniş açıdır. Eğim pozitif değer alıyorsa eğim açısı dar açı, eğim negatif değer alıyorsa eğim açısı geniş acıdır.