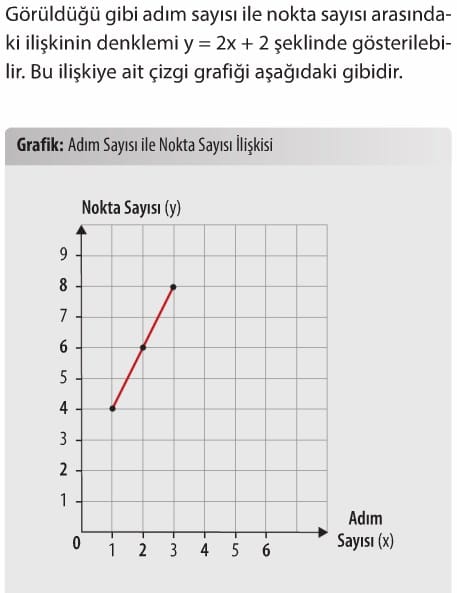
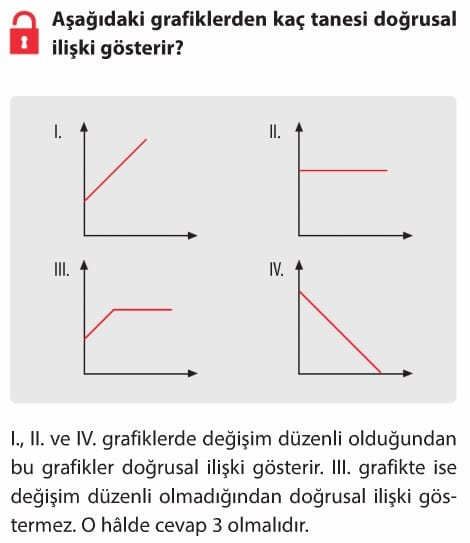
Doğrusal Denklemler Çözümlü Sorular
DETAYLI ÇÖZÜMLÜ SORULAR
SORU 1:
5(2x – 3) + 7 = 3(4 – x) + 2 denklemini çözünüz.
ADIM ADIM ÇÖZÜM:
- Parantezleri dağıtalım:
- 5 × 2x = 10x
- 5 × (-3) = -15
- 3 × 4 = 12
- 3 × (-x) = -3x
Denklem: 10x – 15 + 7 = 12 – 3x + 2
- Benzer terimleri toplayalım:
- Sol taraf: 10x – 8
- Sağ taraf: 14 – 3x
Denklem: 10x – 8 = 14 – 3x
- x’li terimleri bir tarafa, sabitleri diğer tarafa toplayalım:
- 10x + 3x = 14 + 8
- 13x = 22
- x’i yalnız bırakalım:
x = 22/13
Cevap: x = 22/13
SORU 2:
(x + 3)/4 – (2x – 1)/6 = 1 denklemini çözünüz.
ADIM ADIM ÇÖZÜM:
- Paydaları eşitleyelim (EKOK(4,6)=12):
- İlk kesir: 3(x+3)/12
- İkinci kesir: 2(2x-1)/12
Denklem: [3(x+3) – 2(2x-1)]/12 = 1
- Pay kısmını açalım:
- 3x + 9 – 4x + 2 = -x + 11
Denklem: (-x + 11)/12 = 1
- 3x + 9 – 4x + 2 = -x + 11
- Çapraz çarpım yapalım:
- -x + 11 = 12
- x’i çözelim:
- -x = 1 → x = -1
Cevap: x = -1
SORU 3:
3x – [5 – 2(x + 3)] = 4x + 7 denklemini çözünüz.
ADIM ADIM ÇÖZÜM:
- İç parantezi dağıtalım:
- -2 × x = -2x
- -2 × 3 = -6
İfade: 5 – 2x – 6 = -2x – 1
- Ana denklemde yerine koyalım:
3x – (-2x – 1) = 4x + 7 - Parantezi açalım (eksi işareti dikkat!):
3x + 2x + 1 = 4x + 7 - Terimleri toplayalım:
5x + 1 = 4x + 7 - x’leri ve sabitleri ayıralım:
5x – 4x = 7 – 1 → x = 6
Cevap: x = 6
SORU 4:
2x + 5 = |x – 3| denklemini çözünüz.
ADIM ADIM ÇÖZÜM:
- Mutlak değer için iki durum inceleyelim:
Durum 1: x – 3 ≥ 0 (x ≥ 3)
- |x – 3| = x – 3
Denklem: 2x + 5 = x – 3
Çözüm: x = -8 (x ≥ 3 koşulunu sağlamaz, geçersiz)
Durum 2: x – 3 < 0 (x < 3)
- |x – 3| = -(x – 3) = -x + 3
Denklem: 2x + 5 = -x + 3
Çözüm: 3x = -2 → x = -2/3 (x < 3 koşulunu sağlar)
- |x – 3| = x – 3
Cevap: x = -2/3
SORU 5:
Bir kesrin payı, paydasının 2 eksiğidir. Paydasına 1 eklenip payından 3 çıkarılırsa yeni kesir 1/2 oluyor. Bu kesri bulunuz.
ADIM ADIM ÇÖZÜM:
- Kesri tanımlayalım:
- Payda = x
- Pay = x – 2
- Kesir = (x – 2)/x
- Yeni durumu yazalım:
- Yeni payda = x + 1
- Yeni pay = (x – 2) – 3 = x – 5
- Yeni kesir = (x – 5)/(x + 1) = 1/2
- Denklemi çözelim:
2(x – 5) = 1(x + 1)
2x – 10 = x + 1
x = 11 - Orijinal kesri bulalım:
(11 – 2)/11 = 9/11
Cevap: 9/11
ÇÖZÜM STRATEJİLERİ:
- Parantez açarken dağıtma özelliğini doğru uygulayın
- Kesirli denklemlerde paydaları eşitleyin
- Mutlak değerlerde farklı durumları ayrı ayrı inceleyin
- Sözel problemlerde matematiksel ifadeyi doğru kurun
- İşlem sırasını takip edin:
- Parantezler
- Çarpma/Bölme
- Toplama/Çıkarma
Önemli Hatırlatma: Her adımda eşitliğin her iki tarafına aynı işlemi uygulayın!
Daha Basit Sorular:
SORU 1:
3x + 5 = 20 denklemini çözünüz.
Çözüm:
3x = 20 – 5
3x = 15
x = 15 / 3
x = 5
Cevap: 5
SORU 2:
2(x – 4) = 10 denklemini çözünüz.
Çözüm:
2x – 8 = 10
2x = 10 + 8
2x = 18
x = 18 / 2
x = 9
Cevap: 9
SORU 3:
5x – 7 = 3x + 5 denklemini çözünüz.
Çözüm:
5x – 3x = 5 + 7
2x = 12
x = 12 / 2
x = 6
Cevap: 6
SORU 4:
x/3 + 4 = 7 denklemini çözünüz.
Çözüm:
x/3 = 7 – 4
x/3 = 3
x = 3 * 3
x = 9
Cevap: 9
SORU 5:
4(x + 2) = 3x + 15 denklemini çözünüz.
Çözüm:
4x + 8 = 3x + 15
4x – 3x = 15 – 8
x = 7
Cevap: 7
SORU 6:
(2x + 1)/5 = 3 denklemini çözünüz.
Çözüm:
2x + 1 = 3 * 5
2x + 1 = 15
2x = 15 – 1
2x = 14
x = 14 / 2
x = 7
Cevap: 7
SORU 7:
6x – 10 = 2x + 6 denklemini çözünüz.
Çözüm:
6x – 2x = 6 + 10
4x = 16
x = 16 / 4
x = 4
Cevap: 4
ÖNEMLİ KURALLAR:
- Eşitliğin iki tarafına aynı işlem uygulanır
- Parantezli ifadeler önce dağıtılır
- Paydalı ifadelerde çapraz çarpım yapılır
- Bilinmeyenler bir tarafta, sabitler diğer tarafta toplanır