Doğrunun Eğimi ve Doğru Denklemleri 11. Sınıf
Bir Doğrunun Eğim Açısı ve Eğimi
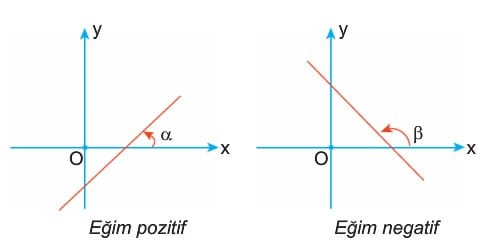
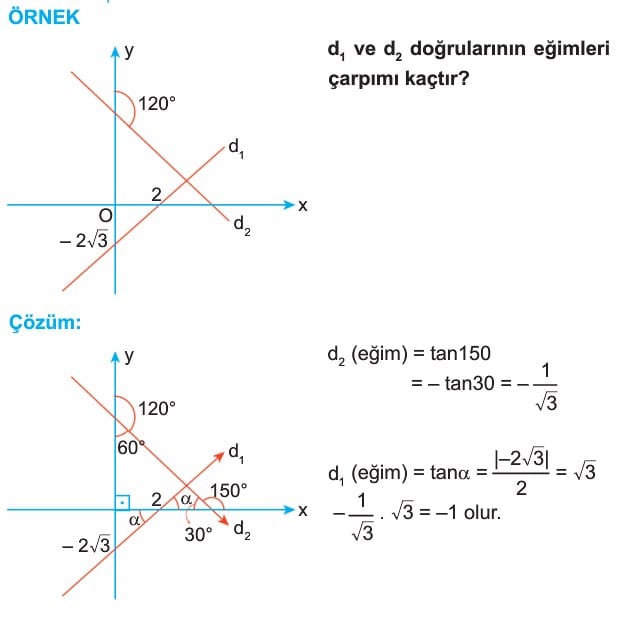
- Bir doğrunun -x ekseni ile pozitif yönde (saat yönünün tersi) yaptığı açıya eğim açısı denir.
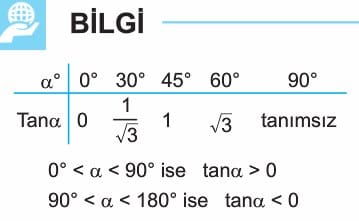
- Eğim açısının tanjantı, o doğrunun eğimini verir.
tanα > 0 eğim sıfırdan büyük
tanβ > 0 eğim sıfırdan küçük
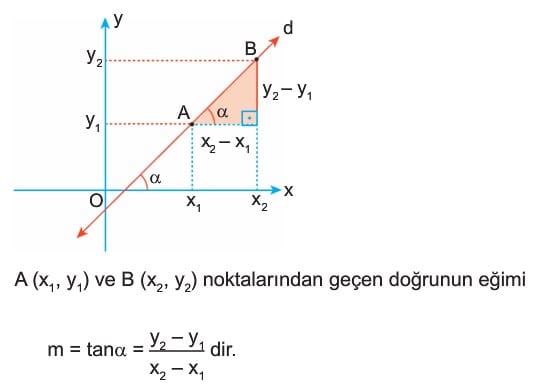
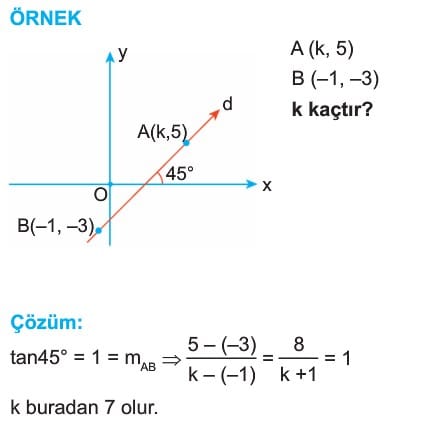
İki Noktası Bilinen Doğrunun Eğimi
Doğru Denklemleri
1) Eğimi ve Bir Noktası Bilinen Doğru Denklemi
2) İki Noktası Bilinen Doğrunun Denklemi
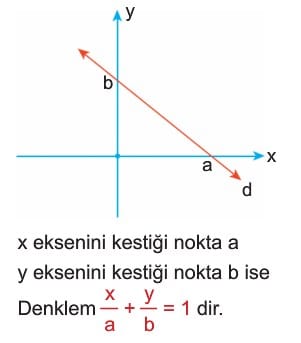
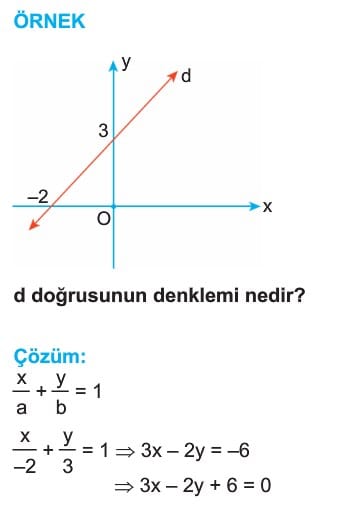
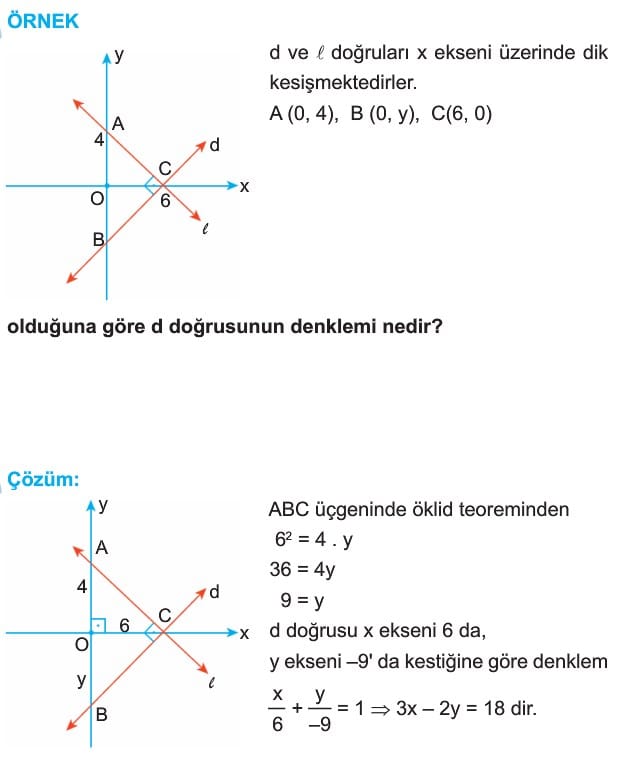
3) Eksenleri Kestiği Noktaları Bilinen Doğrunun Denklemi
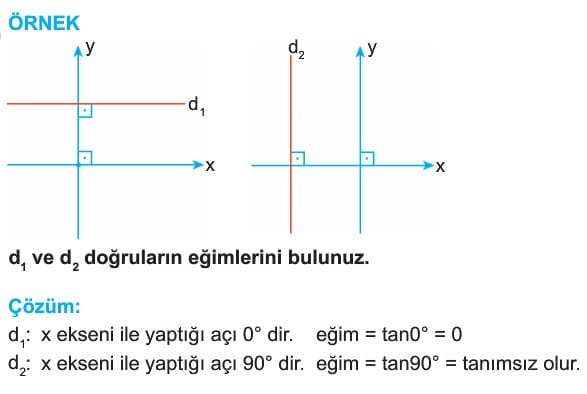
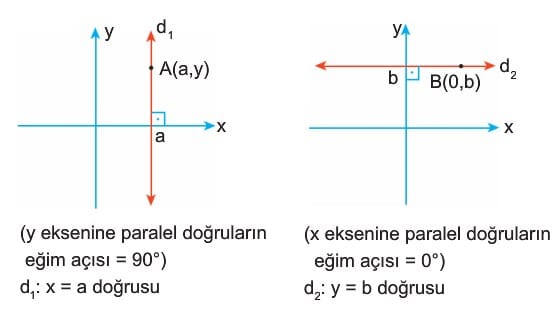
4) Eksenlere Paralel Doğruların Denklemi
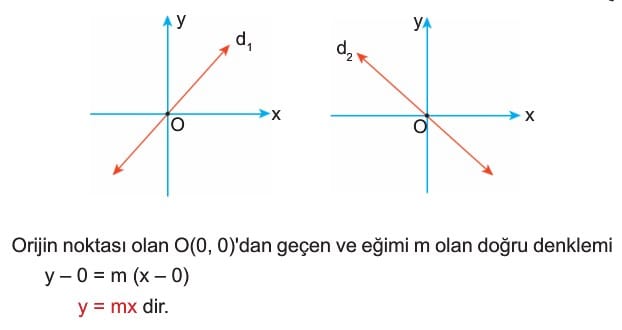
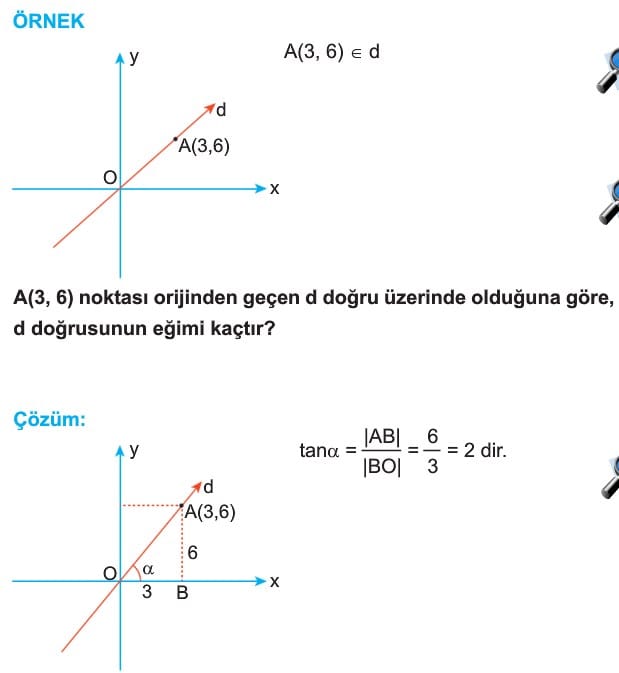
5) Orjinden Geçen Doğru Denklemi
Bilgi: y = x doğrusuna 1. açıortay doğrusu, y = -x doğrusuna da 2. açıortay doğrusu denir.
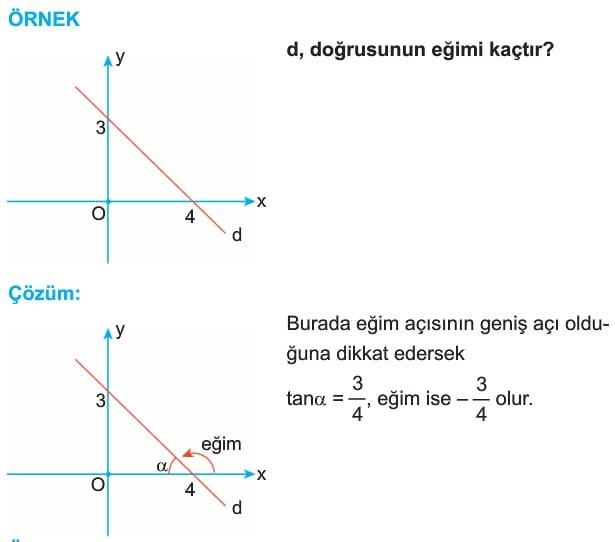
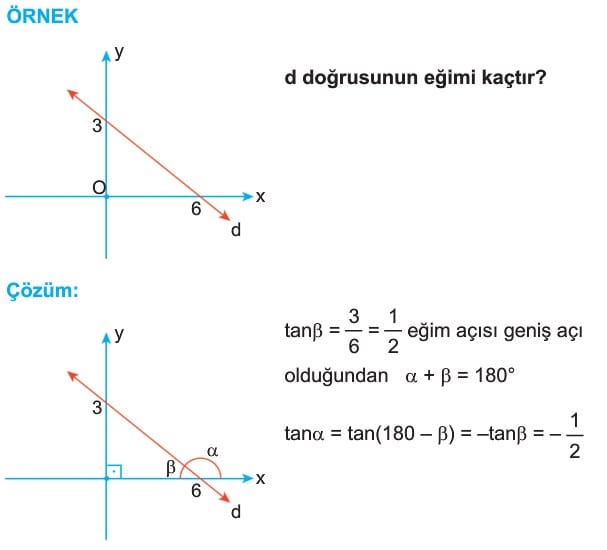
Denklemi Bilinen Doğrunun Eğimi
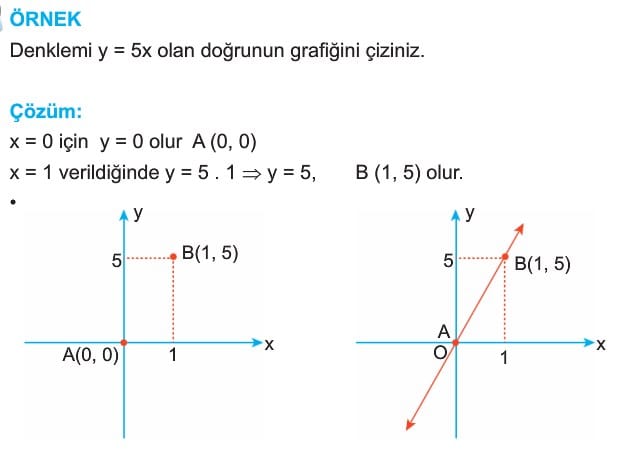
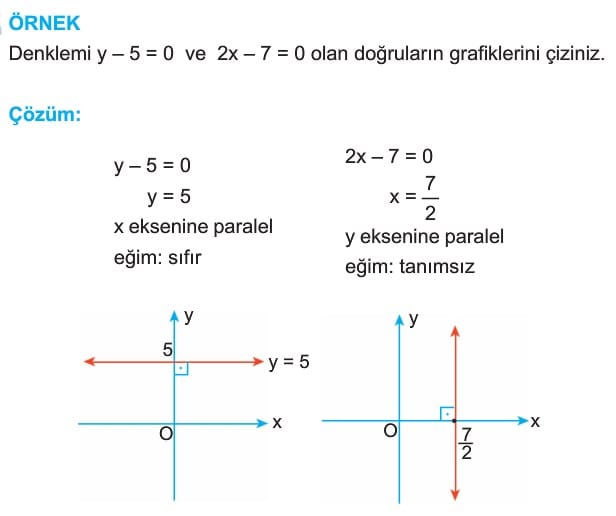
Denklemi Verilen Doğrunun Grafiği
Doğrunun Eğimi ve Doğru Denklemleri Soruları ve Çözümleri
Soru 1
Bir doğru (3, 2) noktasından geçiyor ve eğimi m = 4 olarak veriliyor. Bu doğrunun denklemini bulunuz.
Çözüm:
Doğru bir noktadan geçtiği için eğim–noktadan geçen doğru denklemi formülünü kullanabiliriz:
y – y₁ = m(x – x₁)
y – 2 = 4(x – 3)
y – 2 = 4x – 12
y = 4x – 10
Doğru denklemi: y = 4x – 10
Soru 2
(1, 3) ve (4, 7) noktalarından geçen doğrunun eğimini bulunuz.
Çözüm:
Eğim formülü: m = (y₂ – y₁) / (x₂ – x₁)
m = (7 – 3) / (4 – 1) = 4 / 3
Eğim: 4 / 3
Soru 3
Eğimi 2 olan ve (0, -3) noktasından geçen doğru denklemini bulunuz.
Çözüm:
y – y₁ = m(x – x₁)
y + 3 = 2(x – 0)
y = 2x – 3
Doğru denklemi: y = 2x – 3
Soru 4
Eğimi -1/2 olan ve orijinden geçen doğrunun denklemini yazınız.
Çözüm:
Orijinden geçen doğru denklemi:
y = m * x
Soru 5
A noktasının koordinatları (2, -3) ve B noktasının koordinatları (6, 5) olan bir doğru veriliyor. Bu iki noktadan geçen doğrunun eğimini ve denklemini bulunuz.
Çözüm:
Öncelikle A ve B noktalarından geçen doğrunun eğimini bulmamız gerekiyor. Eğim formülü: m = (y₂ – y₁) / (x₂ – x₁)
A(2, -3) ve B(6, 5) noktaları için x₁ = 2, y₁ = -3, x₂ = 6 ve y₂ = 5 değerlerini yerine koyalım:
m = (5 + 3) / (6 – 2) = 8 / 4 = 2
Eğim 2 olarak bulundu. Şimdi eğim ve bir nokta kullanarak doğrunun denklemini yazabiliriz. A noktasını kullanarak:
y – y₁ = m(x – x₁)
y + 3 = 2(x – 2)
y + 3 = 2x – 4
y = 2x – 7
Doğru denklemi: y = 2x – 7
Soru 6
Bir doğrunun denklemi 3x – 4y + 12 = 0 olarak veriliyor. Bu doğrunun eğimini bulunuz.
Çözüm:
Doğrunun denklemi standart formdadır: Ax + By + C = 0. Bu formdaki bir doğrunun eğimi, m = -A / B formülü ile bulunur.
Bu denklemde A = 3 ve B = -4 olduğundan doğrunun eğimi:
m = -3 / -4 = 3 / 4
Eğim: 3 / 4
Soru 7
Eğim ve bir nokta ile verilen bir doğrunun denklemini bulunuz. Eğimi -1 ve (4, 2) noktasından geçen doğrunun denklemini yazınız.
Çözüm:
Bir noktadan geçen doğrunun denklemi:
y – y₁ = m(x – x₁)
Bu durumda m = -1, x₁ = 4 ve y₁ = 2 olduğundan:
y – 2 = -1(x – 4)
y – 2 = -x + 4
y = -x + 6
Doğru denklemi: y = -x + 6
Soru 8
(0, -1) ve (-2, 3) noktalarından geçen doğrunun eğimini ve denklemini bulunuz.
Çözüm:
Öncelikle eğimi bulalım. Eğim formülü:
m = (y₂ – y₁) / (x₂ – x₁)
y₂ = 3, y₁ = -1, x₂ = -2, x₁ = 0 için:
m = (3 + 1) / (-2 – 0) = 4 / -2 = -2
Eğim -2 olarak bulundu. Şimdi eğim ve bir nokta ile doğru denklemini yazalım. (0, -1) noktasını kullanarak:
y – y₁ = m(x – x₁)
y + 1 = -2(x – 0)
y = -2x – 1
Doğru denklemi: y = -2x – 1