Diziler 12. Sınıf Matematik
Diziler: Pozitif doğal sayılar kümesinden gerçek sayılar kümesine tanımlanan her fonksiyona gerçek sayı dizisi veya dizi denir.
Dizinin Özellikleri
- Her dizinin mutlaka genel terimi vardır. Genel terimi olmayan dizi olmaz.
- Bir dizide genel terim an şeklinde gösterilir. Genel terimi an olan dizi ise (an) şeklinde gösterilir.
- (an) = (a1, a2, a3, …, an, …) dizisinde a1, a2, a3, …, an dizinin terimleridir.
- Bir dizinin tanımlı olabilmesi için tüm pozitif doğal sayılar için tanımlı olmalıdır.
Sonlu Dizi: Tanım kümesi A = {1, 2, 3, …, k), k ∈ N+ olan diziye sonlu dizi denir. Sonlu olmayan dizilere sonsuz dizi denir.
Aritmetik Dizi ve Özellikleri
Aritmetik Dizi Soruları ve Çözümleri
Geometrik Dizi ve Özellikleri
Geometrik Dizi Soruları ve Çözümleri
Diziler konu anlatımı videosu 1
Diziler konu anlatımı videosu 2
Diziler konu anlatımı videosu 3
Çözümlü Örnek Test Soruları
Soru 1
Bir dizinin ilk terimi a₁ = 5 ve her terimi bir önceki terimden 3 fazlaysa, bu dizinin genel terimi aₙ aşağıdakilerden hangisidir?
A) aₙ = 5n
B) aₙ = 3n + 2
C) aₙ = 3n – 3
D) aₙ = 5 + 3(n – 1)
E) aₙ = 2n + 5
Çözüm: Dizinin ilk terimi 5 ve her terim bir öncekinden 3 fazla olduğuna göre, aritmetik dizidir. Genel terim formülü aₙ = a₁ + (n – 1)d olur. Burada d = 3 ve a₁ = 5 olduğundan aₙ = 5 + 3(n – 1). Cevap: D
Soru 2
Bir dizinin genel terimi aₙ = 2n – 1 şeklinde verilmiştir. Bu dizinin 7. terimi kaçtır?
A) 11
B) 12
C) 13
D) 14
E) 15
Çözüm: Genel terimde n = 7 yerine konulursa a₇ = 2(7) – 1 = 14 – 1 = 13. Cevap: C
Soru 3
Bir aritmetik dizinin ilk terimi 4 ve ortak farkı 6’dır. Bu dizinin 5. terimi nedir?
A) 20
B) 24
C) 28
D) 30
E) 34
Çözüm: Aritmetik dizinin genel terimi aₙ = a₁ + (n – 1)d formülüyle bulunur. Burada a₁ = 4 ve d = 6. 5. terim için a₅ = 4 + (5 – 1) × 6 = 4 + 24 = 28. Cevap: C
Soru 4
Bir geometrik dizide ilk terim 3 ve ortak oran 2’dir. Bu dizinin 4. terimi kaçtır?
A) 12
B) 18
C) 24
D) 36
E) 48
Çözüm: Geometrik dizinin genel terimi aₙ = a₁ × rⁿ⁻¹ formülüyle bulunur. Burada a₁ = 3 ve r = 2. 4. terim için a₄ = 3 × 2³ = 3 × 8 = 24. Cevap: C
Soru 5
Bir aritmetik dizide a₃ = 10 ve a₆ = 19 olduğuna göre, ortak fark nedir?
A) 2
B) 3
C) 4
D) 5
E) 6
Çözüm: Aritmetik dizide aₙ = a₁ + (n – 1)d formülü geçerlidir. a₆ – a₃ = (19 – 10) = 3d olduğuna göre, d = 3. Cevap: B
Soru 6
Bir geometrik dizinin 2. terimi 6 ve 4. terimi 24’tür. Bu dizinin ortak oranı nedir?
A) 1
B) 2
C) 3
D) 4
E) 5
Çözüm: Geometrik dizide aₙ = a₁ × rⁿ⁻¹ olduğuna göre, a₄ / a₂ = r² ifadesinden r = 2 bulunur. Cevap: B
Soru 7
Bir dizinin genel terimi aₙ = 5 – 2n şeklinde verilmiştir. Bu dizinin ilk negatif terimi kaçıncı terimdir?
A) 2
B) 3
C) 4
D) 5
E) 6
Çözüm: İlk negatif terimi bulmak için 5 – 2n < 0 eşitsizliğini çözeriz. n > 2.5 çıkar, bu durumda n = 3. Cevap: B
Soru 8
Bir aritmetik dizinin ilk terimi 7, ortak farkı 4’tür. Bu dizideki ilk 5 terimin toplamı kaçtır?
A) 55
B) 60
C) 65
D) 70
E) 75
Çözüm: İlk 5 terimin toplamı S₅ = n/2 × (2a₁ + (n – 1)d) formülüyle bulunur. S₅ = 5/2 × (2 × 7 + (5 – 1) × 4) = 75. Cevap: E
Matematikte kullanılan dizi sözcüğü ile günlük hayatta kullanılan dizi sözcüğü aslında birbirinden çok farklı değildir. “Satranç taşlarını, satranç tahtasına dizmek”, “Ansiklopedi takımını, alfabetik sıraya göre kitaplığa dizmek”, “Bardakları ikişer ikişer rafa dizmek” ifadeleri dizi sözcüğünün günlük hayatta kullanılan örnekleridir.
{1, 2, 3, 4, 5, … }
{2, 4, 6, 8, 10, … }
{5, 10, 15, 20, … }
kümelerinin elemanlarının oluşturduğu dizilim ise dizi sözcüğünün matematiksel anlamda kullanılan örnekleridir. Her iki örnekte de nesnelerin veya sayıların belirli bir kurala göre dizilimi söz konusudur.
Dizi Kavramı: A ≠ Q olmak üzere ƒ:Z+ –> A tanımlı her fonksiyona dizi denir. Diğer bir ifadeyle tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir.
n eleman Z+ için ƒ(n) = an ifadesine dizinin n. terimi veya genel terimi denir.
A = R ise diziye reel sayılar dizisi denir.
Bir reel sayı dizisi,
ƒ = {(1,a1), (2,a2), (3,a3), … , (n,an), …} şeklinde gösterilir. a1, a2, a3 reel sayılarına sırasıyla dizinin birinci, ikinci ve üçüncü terimi denir. Dizi genel terimleri ile belirlidir. Genel terimleri verilmeden yazılan sayı grupları dizi belirtmez.
Sonlu dizi olduğu belirtilmediği sürece her dizinin sonsuz dizi olduğu anlaşılmalıdır.
Bütün terimleri birbirine eşit olan dizilere sabit dizi denir.
Dizi, tanım kümesi sayma sayıları olan bir fonksiyondur. an dizisi bir fonksiyon olduğuna göre fonksiyonun özellikleri dizi için de kullanılabilir.
Genel terimi an olan bir dizide, n yerine terim numarası yazılarak dizinin terimi bulunur.
Bir terimi kendinden önceki bir veya birkaç terim cinsinden tanımlanan dizilere indirgemeli dizi, tanımlama bağıntısına da indirgeme bağıntısı denir.
Ardışık terimleri arasındaki fark aynı sabit sayıya eşit olan dizilere aritmetik dizi denir. Sonlu bir aritmetik dizide baştan ve sondan eşit uzaklıkta bulunan terimlerin toplamı eşittir.
Ardışık terimleri arasındaki oran sabit olan dizilere geometrik dizi denir. Sabit orana ise ortak çarpan denir.
Soru: Bir konveks (dış bükey) beşgenin iç açılarını ölçüleri bir aritmetik dizinin ardışık beş terimidir. Bu beşgenin en büyük açısının ölçüsü 118° olduğuna göre, en küçük açısının ölçüsü kaç derecedir?
A) 98 B) 94 C) 88 D) 86 E) 72
Soru: İlk terimi x, ortak farkı y olan bir aritmetik dizinin 4. ve 7. terimleri bir geometrik dizinin ilk üç terimi olduğuna göre x ile y arasındaki bağıntı aşağıdakilerden hangisidir?
A)x=y B)x=-2y C)x=2y
D) 2x = -3y E) 2x = 3y
Soru: Bir aritmetik dizinin ilk 10 teriminin aritmetik ortalaması 6, ilk 20 teriminin aritmetik ortalaması 16’dır. Buna göre, dizinin 15. terimi kaçtır?
A) 10 B) 15 C) 20 D) 25 E) 30
İndirgemeli Dizi: Her terimi kendinden önceki bazı terimleri türünden yazılabilen dizilere İndirgemeli dizi denir.
Diziler konusu 11. sınıf matematik müfredatında yer almakta olup olasılık konusundan sonra gelen konudur. Dizilerden Lys matematik sınavında soru gelmektedir. Ygs de ise dizilerden soru çıkmamaktadır.
Diziler konu başlıkları;
- Dizinin tanımı
- Sonlu dizi, sonsuz dizi ve sabit dizi tanımları
- Dizilerin eşitliği
- Dizilerde işlemler (Toplama, çıkarma, çarpma, bölme)
- Monoton diziler
- Alt dizi
- Aritmetik dizi ve özellikleri
- Aritmetik dizinin ilk n teriminin toplamı
- Geometrik dizi ve özellikleri
- Geometrik dizinin ilk n teriminin toplamı











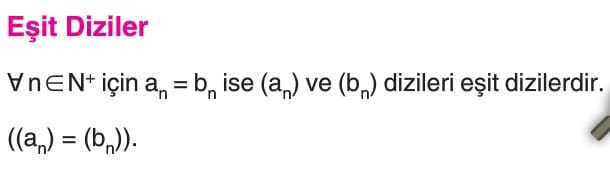








































adamsıınız