Dikdörtgende çevre ve alan problemleri, 5. sınıf matematik dersinde öğrencilerin geometri kavramlarını daha iyi anlamalarını sağlar. Çevre, bir dikdörtgenin etrafını çevreleyen çizginin uzunluğu iken, alan, bu şeklin kapladığı yüzeyin büyüklüğünü ifade eder. Çevre ve alan hesaplamaları, günlük yaşamda sıkça karşımıza çıkar; örneğin, bir bahçeye çit çekmek ya da bir odanın zeminini döşemek için bu hesaplamalar kullanılır. Dikdörtgen çevresi ve alanı problemlerini çözmek, öğrencilere matematiksel düşünme ve problem çözme becerileri kazandırır.
Dikdörtgende Çevre ve Alan Problemleri Testleri
5. Sınıf Dikdörtgende Çevre ve Alan Problemleri Ders Notu
Dikdörtgenin çevre uzunluğu ve alanı ile ilgili problemleri çözmek için şu adımlardan faydalanılabilir:
- Probleme ait matematiksel bileşenler (şekil, uzunluk, alan ölçüleri gibi) belirlenmeli.
- Problemi oluşturan bileşenler şekil üzerine yazılmalı veya probleme ait şekil çizilmeli.
- Dönüştürülen problemde bilinmeyen durumlar ya da istenilenler açıklanmalı.
- İstenilenlerin belirlenmesi için stratejiler belirlenmeli ve sonuca ilişkin tahminler geliştirilmelidir.
- Belirlenen stratejiler çözüm için uygulanmalı ve sonuç ile tahmin karşılaştırılmalıdır.
- Çözüm yolları kontrol edilmeli ve çözüme ulaştırmayacak strateji değiştirilmelidir.
- Kullanılan stratejiler gözden geçirilmeli ve alternatif çözüm yolları belirlenmelidir.
- Kullanılan stratejiler farklı problemlerin çözümlerinde de kullanılabilir.
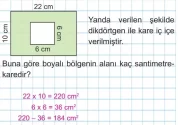
Örnek: Kenar uzunlukları 22 ve 30 cm olan defterin ön kapağına yapıştırılan kare şeklindeki etiketin çevresinin uzunluğu 20 cm’dir. Buna göre, defterin ön kapağında kalan alanın kaç santimetrekare olduğunu bulunuz.
Problem çözme adımlarını kullanarak çözelim.
Problem Bileşenlerini Belirleyelim:
- Problemde dikdörtgen şeklindeki defterin kenar uzunlukları 22 cm ve 30 cm olarak verilmiştir.
- Defterin üzerine çevresi 20 cm olan kare bir etiket yapıştırılmıştır.
Problem bileşenlerini kullanarak aşağıdaki şekli çizebiliriz.
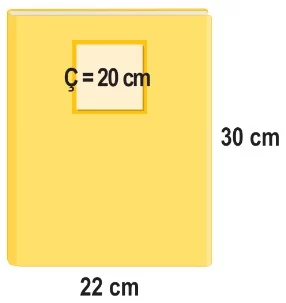
Problemde etiket yapıştırıldıktan sonraki alan istenmektedir.
Strateji 1: Çözüm için önce defterin alanı bulunup ardından etiketin alanı çıkarılabilir.
- Etiketin bir kenar uzunluğunu bulalım, alan ölçüsünü hesaplayalım.
Etiketin Alan Ölçüsü = 5 × 5 = 25 cm²
Kapak Alan Ölçüsü = 30 × 22 = 660 cm²
Kalan Alan = Defter Kapağının Alanı – Etiket Alanı
= 660 – 25 = 635 cm²
- Çözüm stratejileri gözden geçirilir.
Etiket ortaya değil de tam köşeye yapıştırılırsa aşağıdaki şekil oluşur.
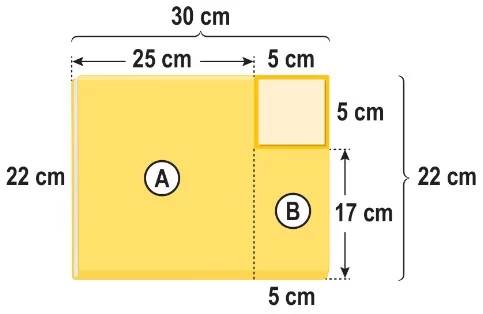
Kalan alan A ve B bölgelerinin alanlarının toplamıdır.
A: 22 cm x 25 cm = 550 cm²
B: 17 cm x 5 cm = 85 cm²
Bu durumda kalan alan: 550 cm² + 85 cm² = 635 cm² olur.
Aynı sonuçlar bulunduğuna göre alan hesaplamalarında benzer yollar kullanılabilir.
