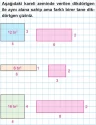
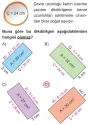
Dikdörtgende Çevre ve Alan İlişkisi 5. Sınıf Matematik

5. Sınıf Matematik Konuları Konu Anlatımları Matematik

10.10.2024

Dikdörtgenin çevresi ve alanı, geometri derslerinde sıklıkla karşılaşılan iki temel kavramdır. Çevre, bir şeklin etrafını saran çizginin toplam uzunluğunu ifade ederken, alan, şeklin kapladığı yüzeyin büyüklüğünü ifade eder. Dikdörtgende çevre ve alan arasındaki ilişki, bazen farklı ölçülerde dikdörtgenlerin aynı çevreye sahip olabileceği, ancak farklı alanlara sahip olabileceği gibi durumları anlamamıza yardımcı olur. Bu konu, öğrencilerin şekillerin özelliklerini daha derinlemesine kavramalarını sağlar.

5. Sınıf Dikdörtgende Çevre ve Alan İlişkisi Testleri

5. Sınıf Dikdörtgende Çevre ve Alan İlişkisi Ders Notu

Alanları Aynı Olan Dikdörtgenler

Aynı alan ölçüsüne sahip dikdörtgenler farklı çevre uzunluklarına sahip olabilir.

Örnek: Alanı 18 cm² olan ve kenar uzunlukları santimetre cinsinden birer doğal sayı olan tüm dikdörtgenleri aşağıdaki tabloda gösterelim.

Alan (cm²)	Ardışık İki Kenarın Uzunlukları	Çevre Uzunluğu (cm)
18	1 x 18	2 x (1 + 18) = 2 x 19 = 38
18	2 x 9	2 x (2 + 9) = 2 x 11 = 22
18	3 x 6	2 x (3 + 6) = 2 x 9 = 18

Alanı 18 cm² olan 3 farklı dikdörtgen çizilebilir.

Örnek: Alanı 30 cm² ve kenar uzunlukları santimetre cinsinden birer doğal sayı olan tüm dikdörtgenleri belirleyerek kenar uzunluklarını aşağıdaki tabloya yazınız.

Tablo: Dikdörtgenlerin Kenar Uzunlukları

Kısa Kenar Uzunluğu (cm)	1	2	3	5
Uzun Kenar Uzunluğu (cm)	30	15	10	6

Çevre Uzunlukları Aynı Olan Dikdörtgenler

Aynı çevre uzunluğuna sahip dikdörtgenler farklı alan ölçülerine sahip olabilir.

Örnek: Çevre uzunluğu 18 cm ve kenar uzunlukları santimetre cinsinden birer doğal sayı olan dikdörtgenlerin kenar uzunlukları ile alanlarını aşağıdaki tabloda gösterelim.

Çevre Uzunluğu (cm)	Ardışık İki Kenarın Uzunlukları (cm)	Alan (cm²)
18	1 x 8	1 x 8 = 8
18	2 x 7	2 x 7 = 14
18	3 x 6	3 x 6 = 18
18	4 x 5	4 x 5 = 20

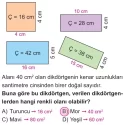
Örnek: Çevre uzunluğu 40 m olan dikdörtgen şeklindeki bir bahçenin kenar uzunlukları metre cinsinden birer doğal sayıdır. Bu bahçenin kenar uzunluklarının alabileceği değerleri ve alanlarını bularak aşağıdaki tabloyu doldurunuz.

Çevre Uzunluğu (m)	Ardışık İki Kenarın Uzunlukları (m)	Alan (m²)
40	1 x 19	19
40	2 x 18	36
40	3 x 17	51
40	4 x 16	64
40	5 x 15	75
40	6 x 14	84
40	7 x 13	91
40	8 x 12	96
40	9 x 11	99
40	10 x 10	100

Alanı Verilen Dikdörtgenin Çevre Uzunluğunu Bulma

Aynı alana sahip farklı dikdörtgenlerin çevre uzunlukları farklı olabilir.

Örnek: Aşağıda alanları 12 br² olan farklı dikdörtgenlerin çevre uzunluklarını bulalım.

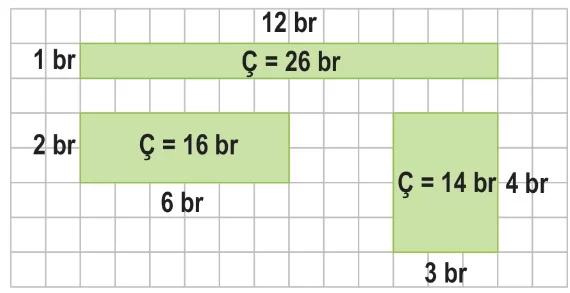
Alanı verilen dikdörtgenin istenilen çevre uzunluğunu bulmak için kenarlardan birinin uzunluğu bilinmelidir. Kenar uzunlukları bilinmediğinde birden fazla dikdörtgen inceleyerek ve birden fazla çevre uzunluğuna sahip dikdörtgen oluşturabiliriz.

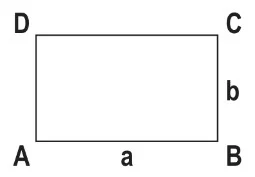
Alan: A(ABCD) = a x b
Çevre: Ç(ABCD) = 2 x (a + b)

Çevre Uzunluğu Verilen Dikdörtgenin Alanını Bulma

Aynı çevre uzunluğuna sahip dikdörtgenlerin farklı alan ölçüleri bulunabilir.

Örnek: Çevre uzunluğu 12 br olan dikdörtgenlerin alanları farklı olabilir.

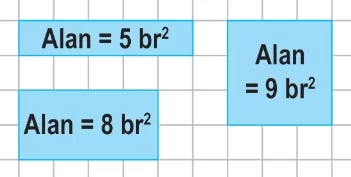
Çevre uzunluğu verilen dikdörtgenlerin istenilen alan ölçüsünü bulmak için kenar uzunluklarından birinin uzunluğu bilinmelidir. Kenar uzunlukları bilinmediğinde birden fazla dikdörtgen inceleyerek birden fazla alana sahip dikdörtgen oluşturabiliriz.