Konunun altında ders videoları bulunmaktadır. (Şenol Hoca, Hocalara Geldik, Ekol Hoca, İsabet Akademi)

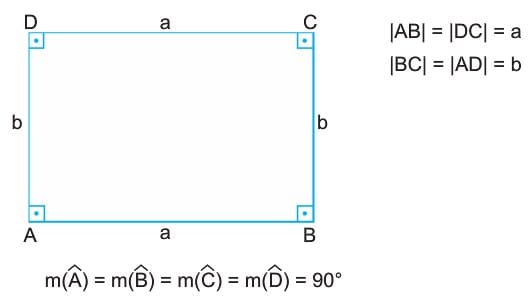
Karşılıklı kenar uzunlukları eşit ve bütün açıları 90° olan dörtgene dikdörtgen denir.

Dikdörtgenin karşılıklı kenarları paralel olduğundan paralelkenarın özelliklerini taşır.
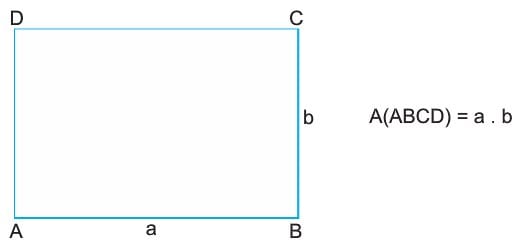
Çevre(ABCD) = 2(a + b) dir.

DİKDÖRTGENİN ÖZELLİKLERİ

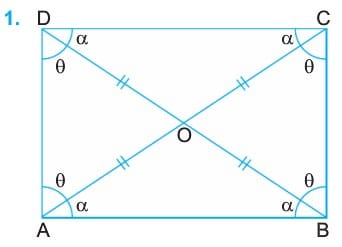
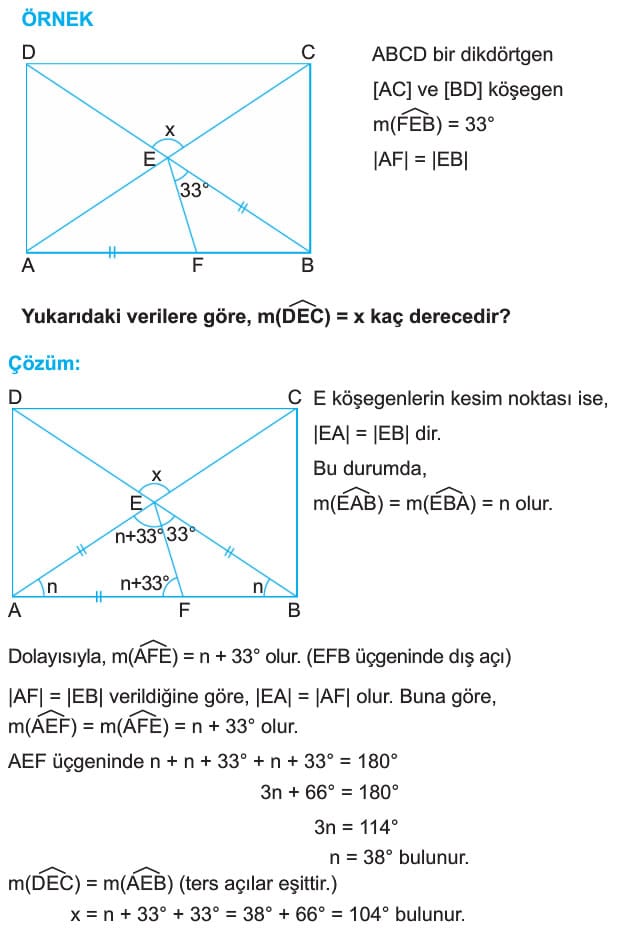
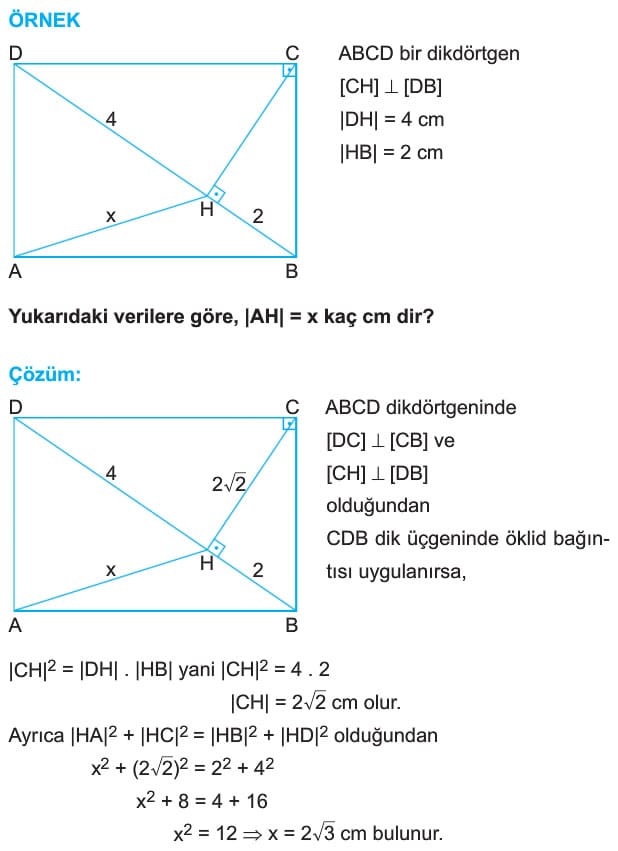
ABCD dikdörtgeninde [AC] ve [BD] köşegen ise,
|OA| = |OB| = |OC| = |OD| dir.

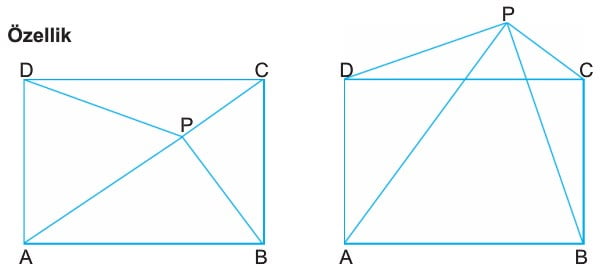
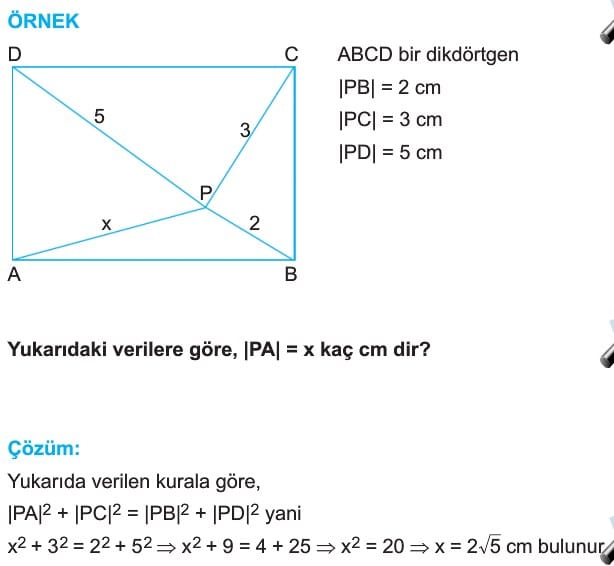
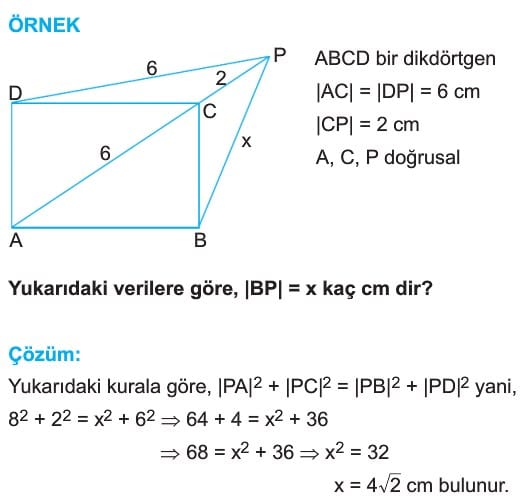
P, ABCD dikdörtğeninin içinde veya dışında bu nokta ise,
|PA|² + |PC|² = |PB|² + |PD|² dir.

Çözümlü Sorular

DİKDÖRTGENDE ALAN

Dikdörtgenin alanı kısa kenarı ile uzun kenarının uzunluklarının çarpımına eşittir.

Çözümlü Sorular

Dikdörtgen Hocalara Geldik

Dikdörtgen Şenol Hoca

Dikdörtgen Ekol Hoca

Çözümlü Örnek Test Soruları

1. Bir dikdörtgenin kısa kenarının uzunluğu 8 santimetre, uzun kenarının uzunluğu 12 santimetredir. Bu dikdörtgenin çevresi kaç santimetredir?
A) 20
B) 32
C) 40
D) 48
Çözüm:
Dikdörtgenin çevresi, iki çarpı kısa kenar artı uzun kenar formülü ile bulunur.
İki çarpı (8 artı 12) eşittir iki çarpı 20 eşittir 40 santimetre.
Doğru cevap: C

---

2. Alanı 60 santimetrekare olan bir dikdörtgenin kısa kenar uzunluğu 6 santimetredir. Uzun kenar uzunluğu kaç santimetredir?
A) 8
B) 10
C) 12
D) 14
Çözüm:
Dikdörtgenin alanı, kısa kenar çarpı uzun kenar formülü ile bulunur.
6 çarpı uzun kenar eşittir 60. Uzun kenar eşittir 60 bölü 6 eşittir 10 santimetre.
Doğru cevap: B

---

3. Bir dikdörtgenin köşegen uzunluğu 13 santimetre, kısa kenar uzunluğu 5 santimetredir. Uzun kenar uzunluğu kaç santimetredir?
A) 9
B) 10
C) 12
D) 14
Çözüm:
Dikdörtgende köşegen uzunluğu Pisagor teoremi ile bulunur.
Köşegenin karesi eşittir kısa kenarın karesi artı uzun kenarın karesi.
13 çarpı 13 eşittir 5 çarpı 5 artı uzun kenarın karesi.
169 eşittir 25 artı uzun kenarın karesi.
Uzun kenarın karesi eşittir 144. Uzun kenar eşittir 12 santimetre.
Doğru cevap: C

---

4. Bir dikdörtgenin çevresi 36 santimetre ve kısa kenarı 8 santimetredir. Uzun kenarı kaç santimetredir?
A) 10
B) 12
C) 14
D) 16
Çözüm:
Dikdörtgenin çevresi iki çarpı kısa kenar artı uzun kenar formülü ile bulunur.
36 eşittir iki çarpı (8 artı uzun kenar).
36 eşittir 16 artı iki çarpı uzun kenar.
İki çarpı uzun kenar eşittir 20. Uzun kenar eşittir 10 santimetre.
Doğru cevap: A

---

5. Bir dikdörtgenin kısa kenarı, uzun kenarının yarısı kadardır. Dikdörtgenin uzun kenarı 16 santimetre ise alanı kaç santimetrekaredir?
A) 64
B) 96
C) 128
D) 192
Çözüm:
Kısa kenar 16 bölü 2 eşittir 8 santimetre.
Dikdörtgenin alanı, kısa kenar çarpı uzun kenar formülü ile bulunur.
8 çarpı 16 eşittir 128 santimetrekare.
Doğru cevap: C

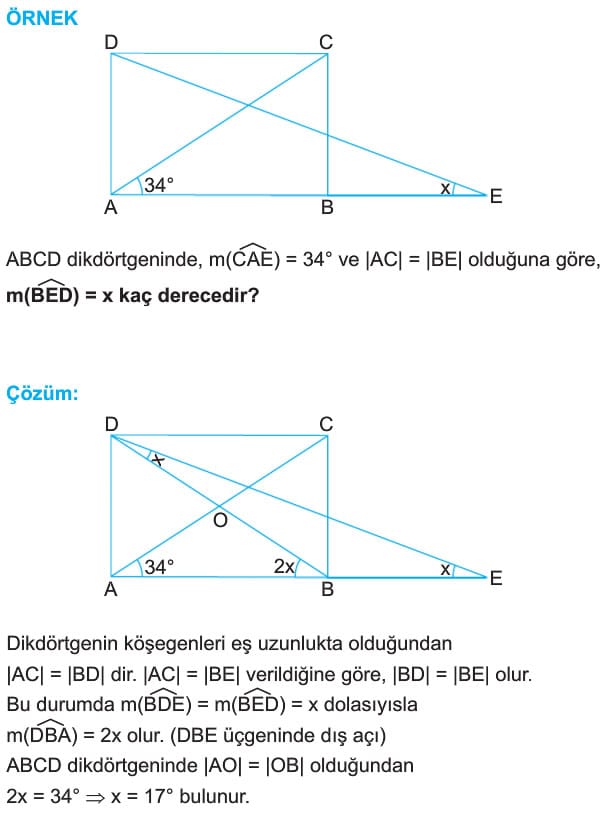
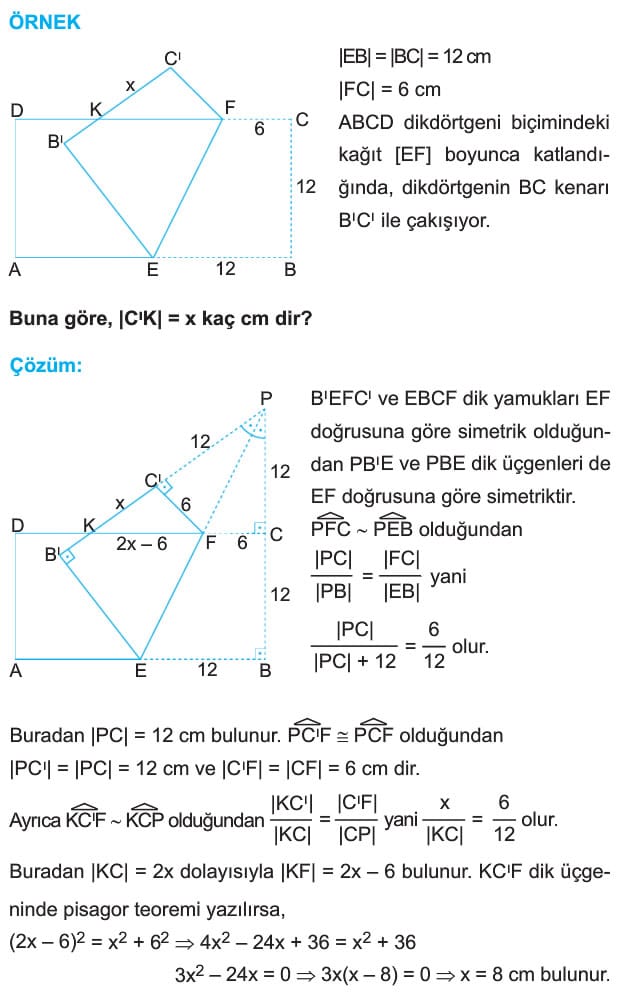
• ABCD dikdörtgeninde köşegenler birbirini 4 eşit parçaya ayırırlar.
• Dikdörtgenler paralelkenara ait olan tüm özelliklere sahiptirler.
• ABCD dikdörtgeninin içinde veya dışında alınan bir P noktasının karşılıklı köşelere olan uzaklıklarının kareleri toplamı birbirine eşittir.

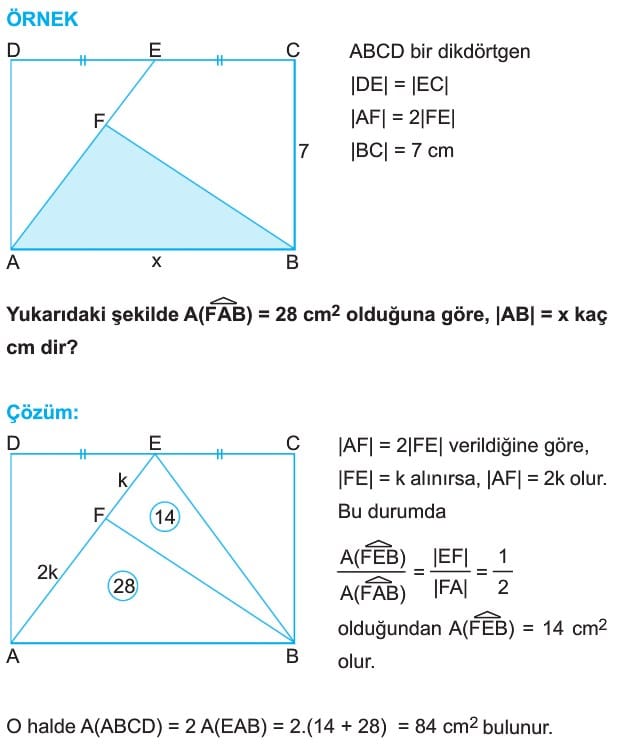
ÖRNEK: Uzun kenarı kısa kenarının 2 katı olan bir dikdörtgenin çevresi 36 cm olduğuna göre, alanı kaç cm² dir?
Çözüm: Uzun kenar kısa kenarın 2 katı verildiğine göre,
|AB| = 2x,
|BC| = x olsun.
Çevre(ABCD) = 36 cm ise,
2.(2x+x) = 36 ise 6x = 36
x = 6 cm olur.
|AB| = 2x = 12 cm ve |BC| = x = 6 cm olduğundan
A(ABCD) = |AB| . |BC| = 12.6 = 72 cm² bulunur.

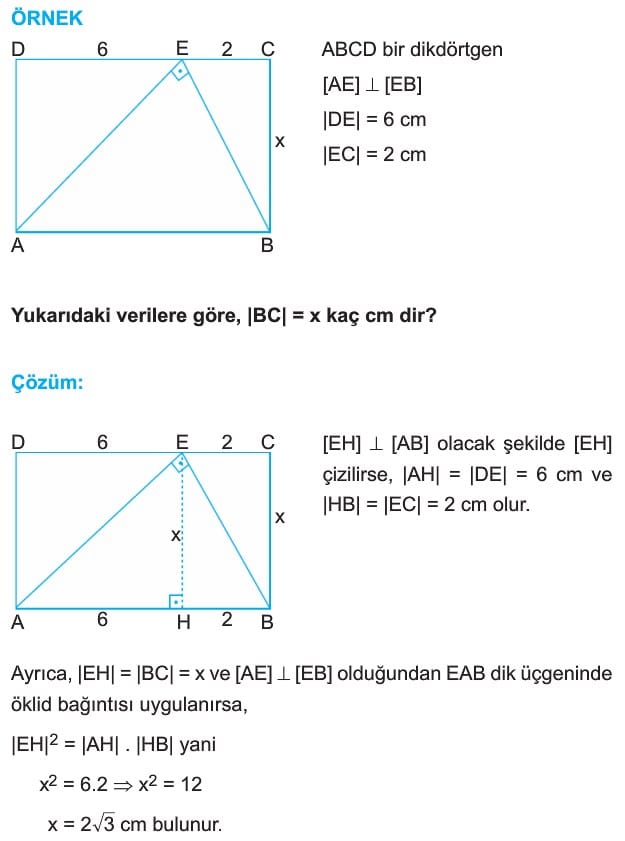
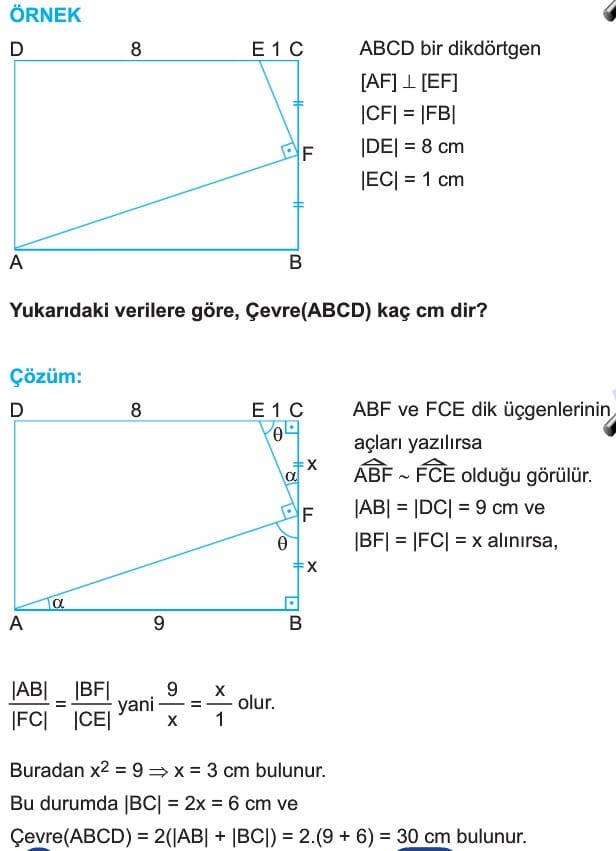
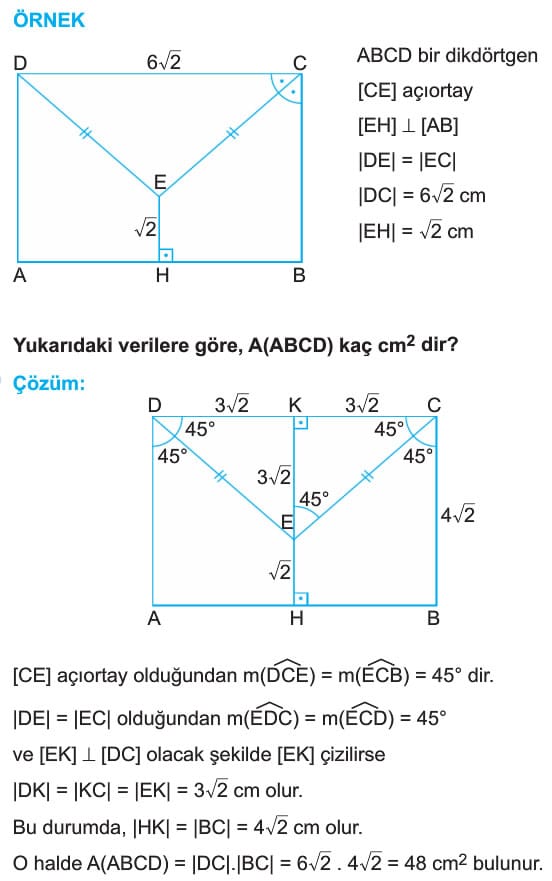
ÖRNEK: ABCD bir dikdörtgen
[CE] açıortay
[EH] dik [AB]
|DE| = |EC|
|DC| = 6√2 cm
|EH| = √2 cm
Yukarıdaki verilere göre, A(ABCD) kaç cm² dir?
Çözüm: [CE] açıorîay olduğundan m(DCE) = m(ECB) = 45° dir.
|DE| = |EC| olduğundan m(EDC) = m(ECD) = 45°
ve [EK] dik [DC] olacak şekilde [EK] çizilirse
|DK| = |KC| = |EK| = 3√2 cm olur.
Bu durumda, |HK| = |BC| = 4√2 cm olur.
O halde A(ABCD) = |DC|.|BC| = 6√2 . 4√2 = 48 cm² bulunur.

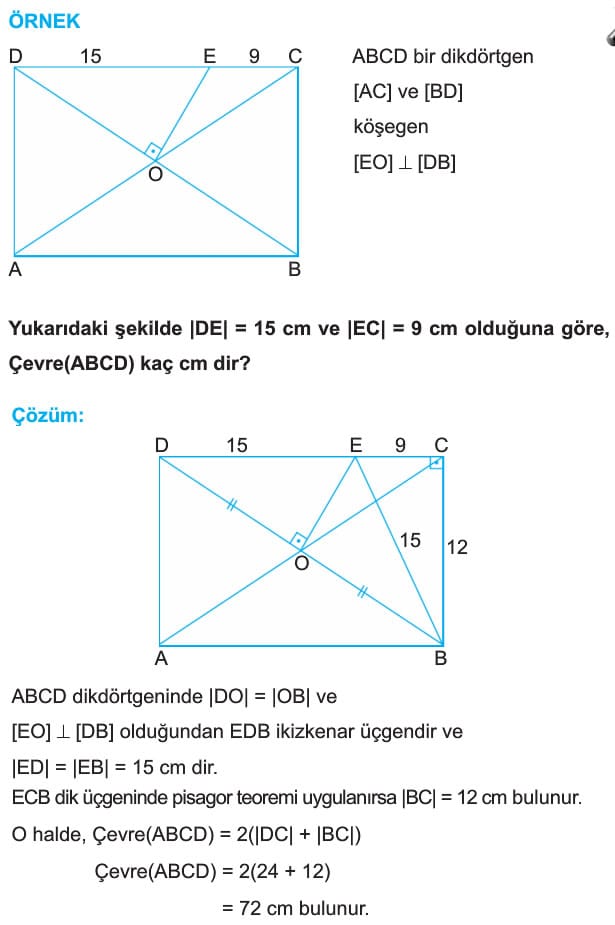
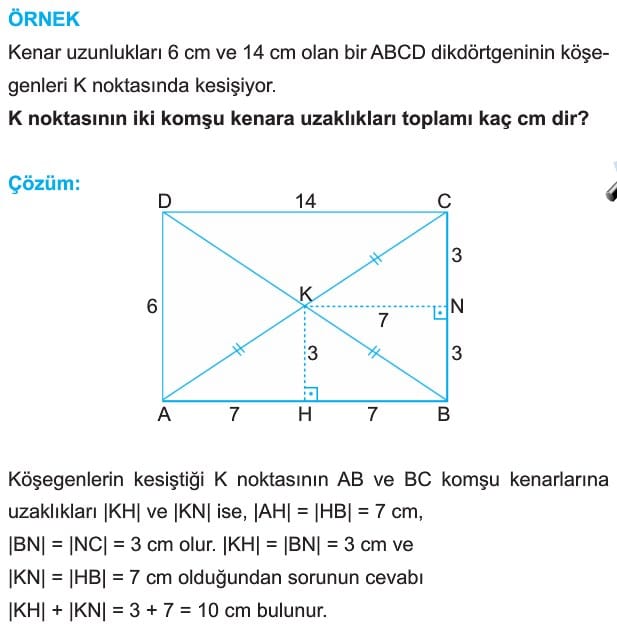
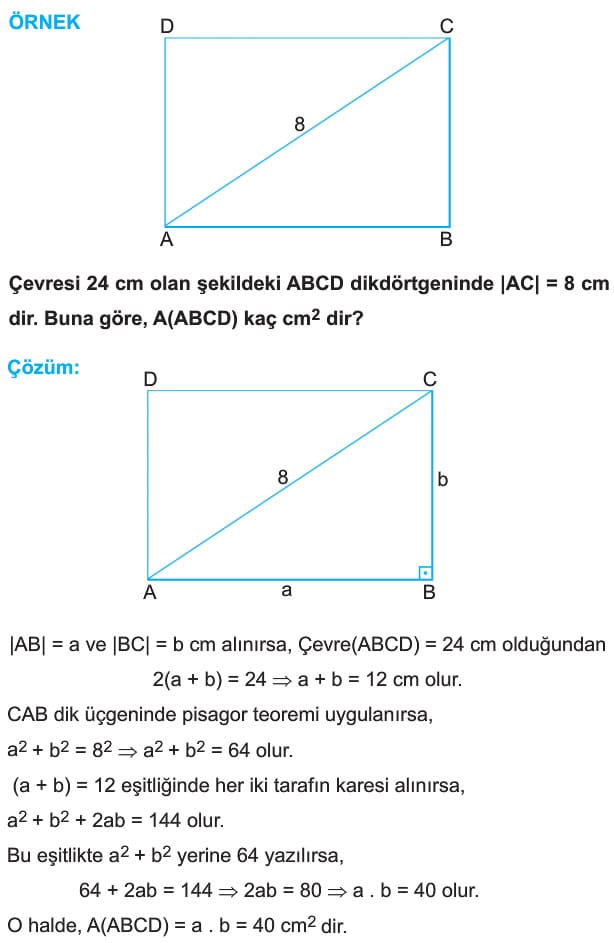
ÖRNEK: Çevresi 24 cm olan şekildeki ABCD dikdörtgeninde |AC| = 8 cm dir. Buna göre, A(ABCD) kaç cm² dir?
Çözüm:|AB| = a ve |BC| = b cm alınırsa, Çevre(ABCD) = 24 cm olduğundan
2(a+b)=24 ise a + b = 12 cm olur.
CAB dik üçgeninde pisagor teoremi uygulanırsa,
a2 + b2 = 82 ise a2 + b2 = 64 olur.
(a + b) = 12 eşitliğinde her iki tarafın karesi alınırsa,
a2 + b2 + 2ab = 144 olur.
Bu eşitlikte a2 + b2 yerine 64 yazılırsa,
64 + 2ab = 144 ise 2ab = 80 ise a.b=40 olur.
O halde, A(ABCD) = a. b = 40 cm2 dir.

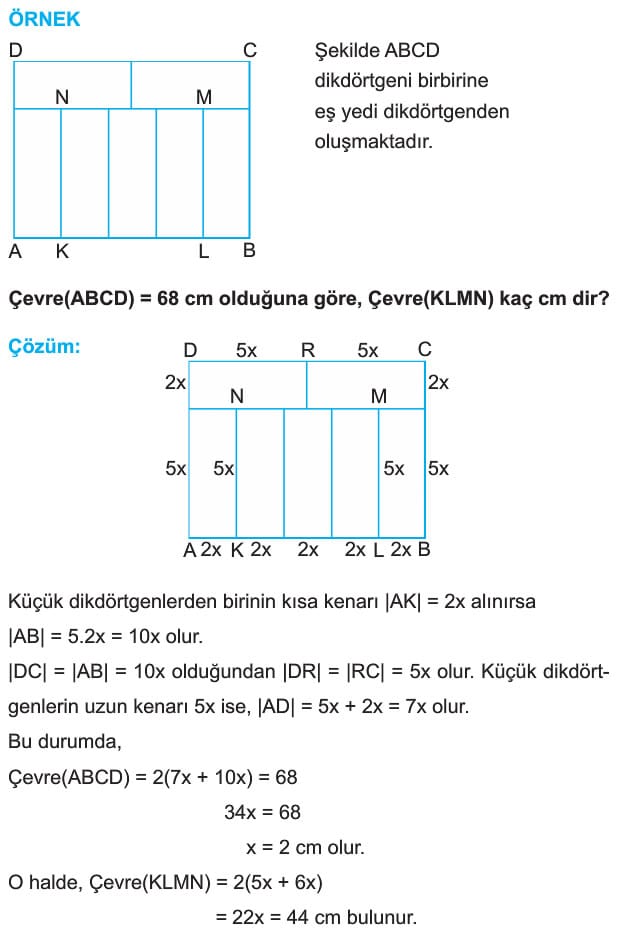
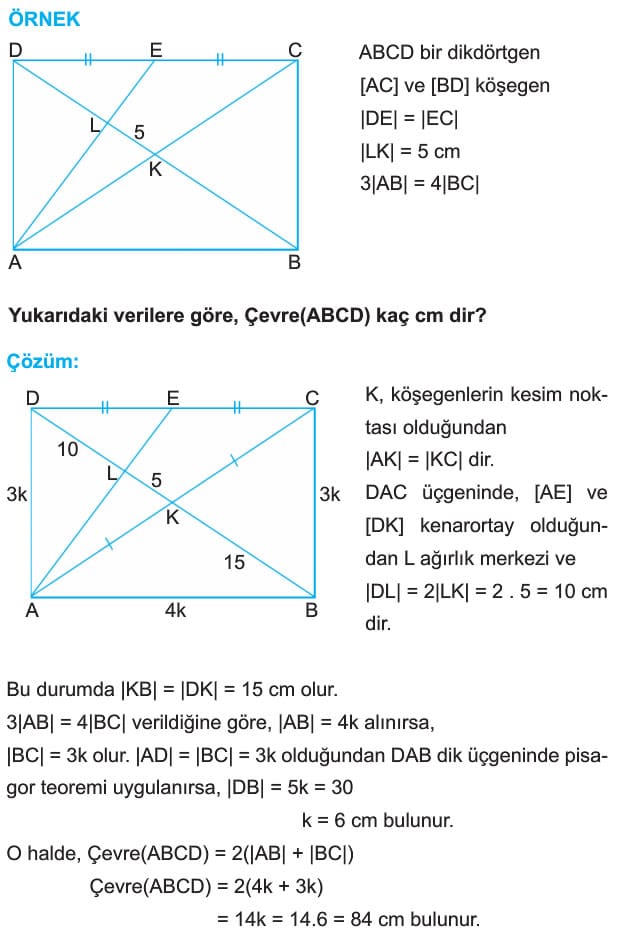
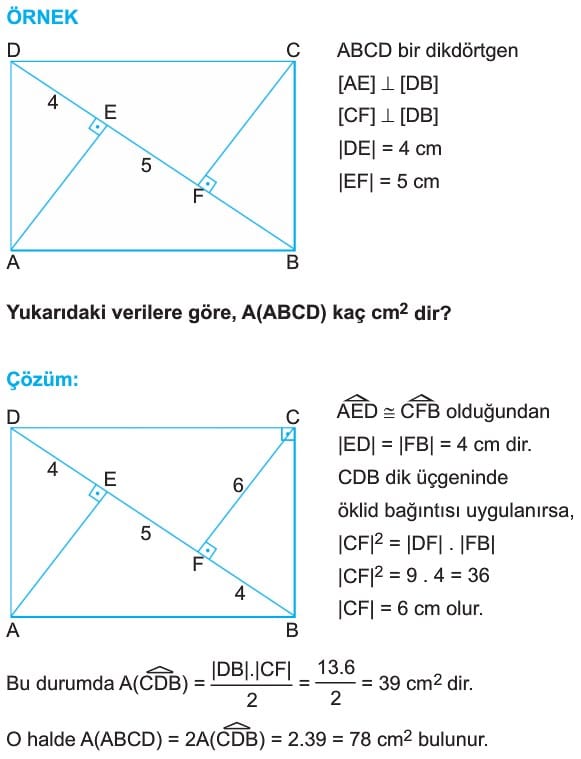
ÖRNEK: ABCD bir dikdörtgen
[AC] ve [BD] köşegen
|DE| = |EC|
|LK| = 5 cm
3|AB| = 4|BC|
Yukarıdaki verilere göre, Çevre(ABCD) kaç cm dir?
Çözüm: K, köşegenlerin kesim noktası olduğundan |AK| = |KC| dir.
DAC üçgeninde, [AE] ve [DK] kenarortay olduğundan L ağırlık merkezi ve
|DL| = 2|LK| =2 . 5 = 10 cm dir.
Bu durumda |KB| = |DK| = 15 cm olur.
3|AB| = 4|BC| verildiğine göre, |AB| = 4k alınırsa,
|BC| = 3k olur. |AD| = |BC| = 3k olduğundan DAB dik üçgeninde pisagor teoremi uygulanırsa, |DB| = 3k = 30
k = 6 cm bulunur.
O halde, Çevre(ABCD) = 2(|AB| + |BC|)
Çevre(ABCD) = 2(4k + 3k) = 14k = 14.6 = 84 cm bulunur.

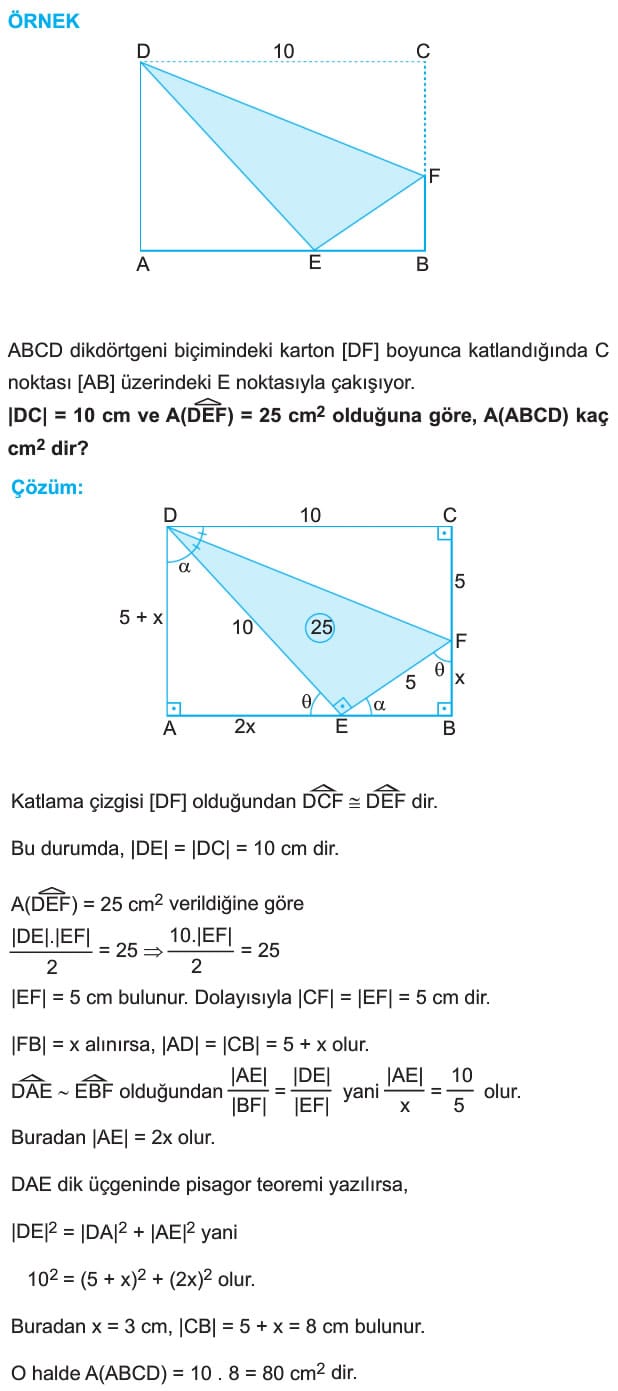
11. sınıf geometri dersi müfredatında bulunan dikdörtgenler konusuyla ilgili kpss, ygs ve lys matematik sınavlarında soru gelebilmektedir. Dikdörtgenler konu anlatımı videosu konu başlıkları,

• Dikdörtgen nedir, tanımı
• Dikdörtgenin kenar, açı ve köşegenlerine ait özellikler
• Dikdörtgende alan bağıntısı
• Dikdörtgenler örnek soru çözümü