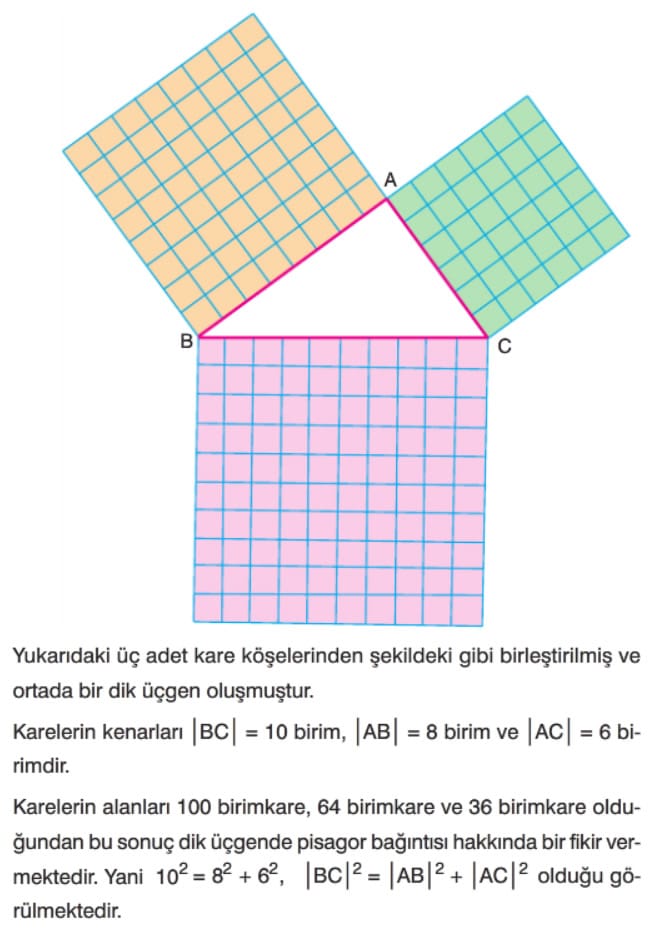
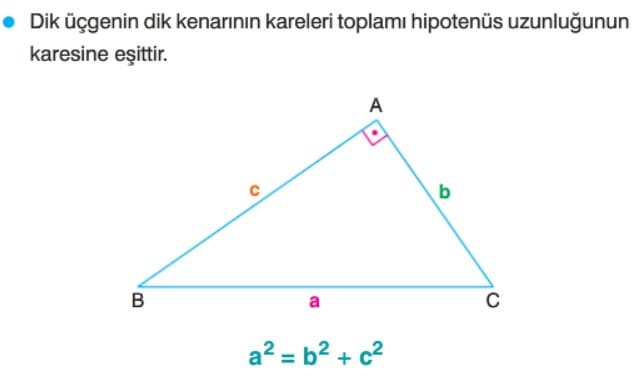
Pisagor Teoremi, dik üçgenlerin temel bir özelliğini açıklayan en önemli geometrik kurallardan biridir. Bu teoreme göre, bir dik üçgende hipotenüsün karesi, dik kenarların kareleri toplamına eşittir. Matematiksel olarak, a² + b² = c² veya “a kare + b kare = c kare” şeklinde ifade edilir. Bu özellik, mühendislikten haritalamaya kadar birçok alanda kullanılır. Özellikle gerçek hayatta mesafeleri ölçme, doğru oranlar belirleme ve benzerlik kurallarını anlamada temel bir araçtır.

Tales, Öklid ve Pisagor Teoremleri Testleri

---

Pisagor Teoremi Ders Notu (Yeni Müfredat)

 

Pisagor Teoremi’nin Uygulamaları:

• Mesafe Hesaplamaları: Pisagor Teoremi, iki nokta arasındaki mesafeyi bulmak için kullanılabilir. Örneğin, bir dik üçgende iki kenarın uzunlukları biliniyorsa, hipotenüs uzunluğu bu teoremle hesaplanabilir.
• Mimari ve Mühendislik Uygulamaları: İnşaat ve mühendislik alanlarında, yapıların yüksekliğini veya uzunluğunu belirlemek için Pisagor Teoremi yaygın olarak kullanılır. Dik açılarla çalışan herhangi bir yapı veya mekanik sistem bu teoremden yararlanabilir.
• Harita ve Navigasyon: Harita üzerinde iki nokta arasındaki doğrudan mesafeyi bulmak için Pisagor Teoremi kullanılır. Özellikle koordinat sistemlerinde mesafe hesaplamalarında bu teorem çok etkilidir.

Çözümlü Sorular

Kenarlarına Göre Özel Dik Üçgenler

3-4-5 Dik Üçgeni

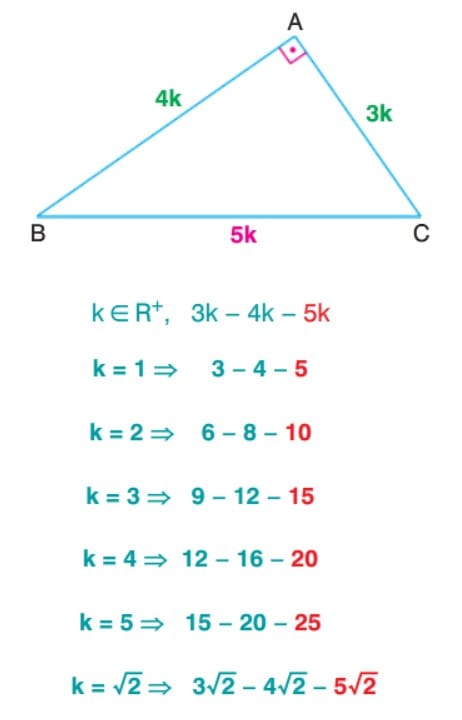
5-12-13 Dik Üçgeni

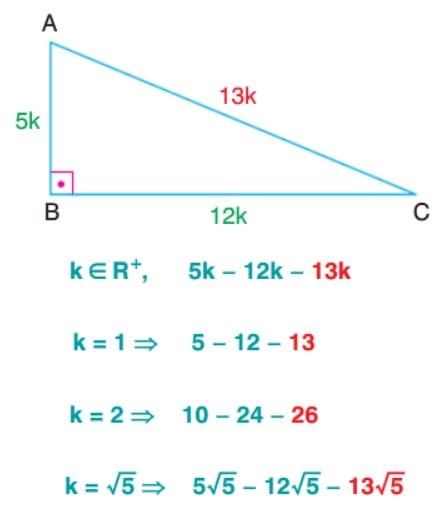
8-15-17 Dik Üçgeni

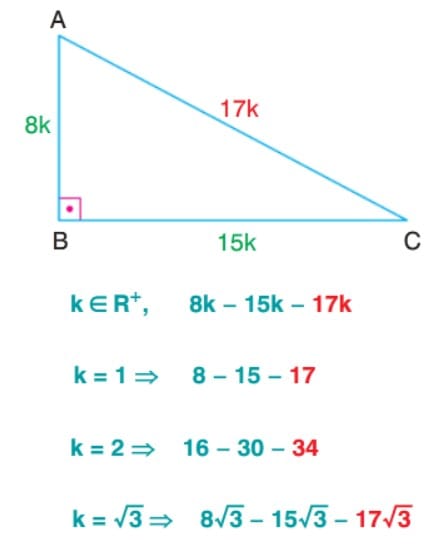
7-24-25 Dik Üçgeni

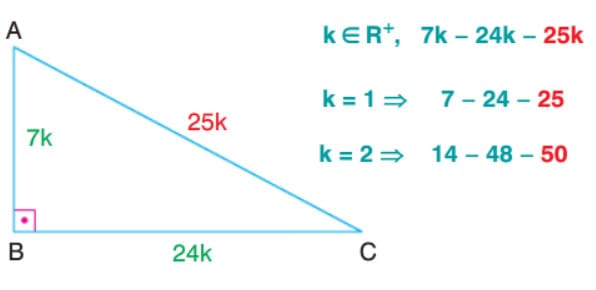
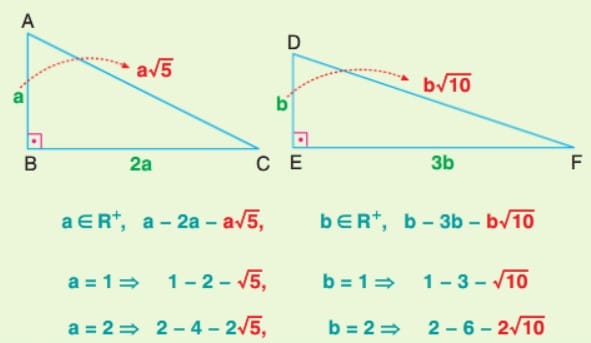
Çözümlü Sorular

Açılarına Göre Özel Üçgenler

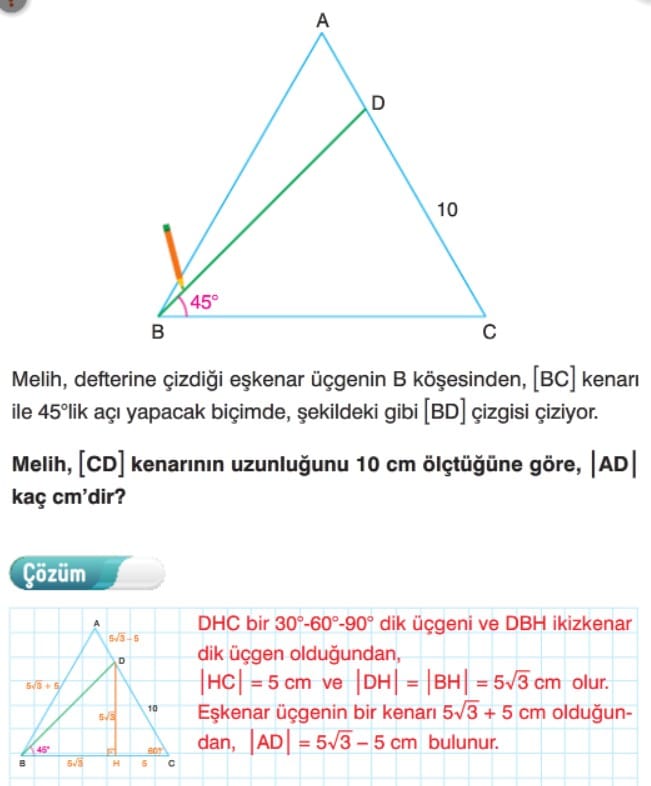
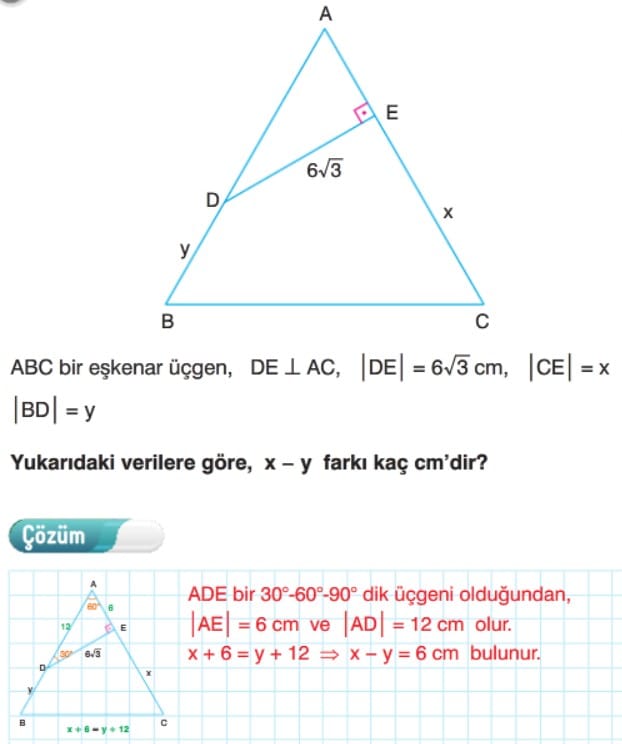
30-60-90 Dik Üçgeni

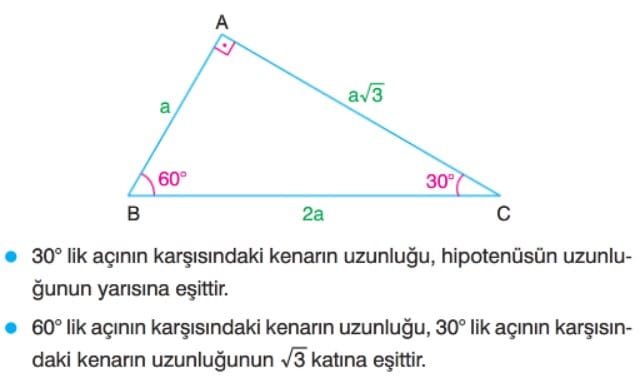
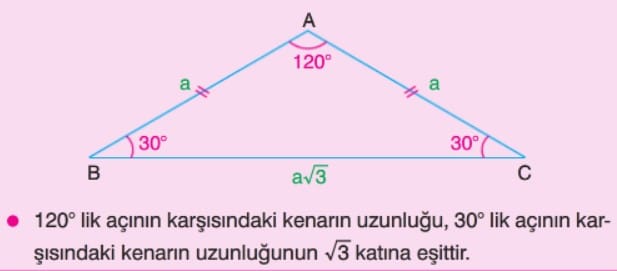
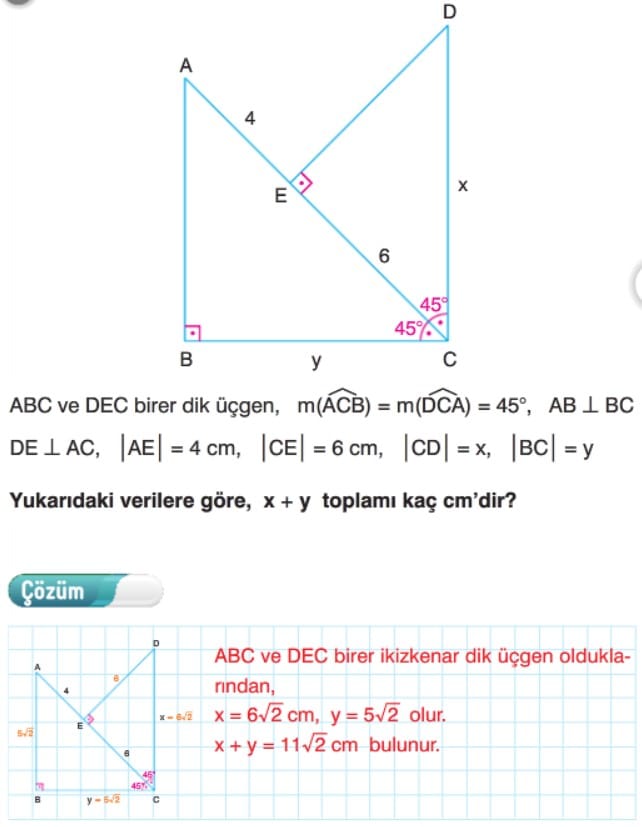
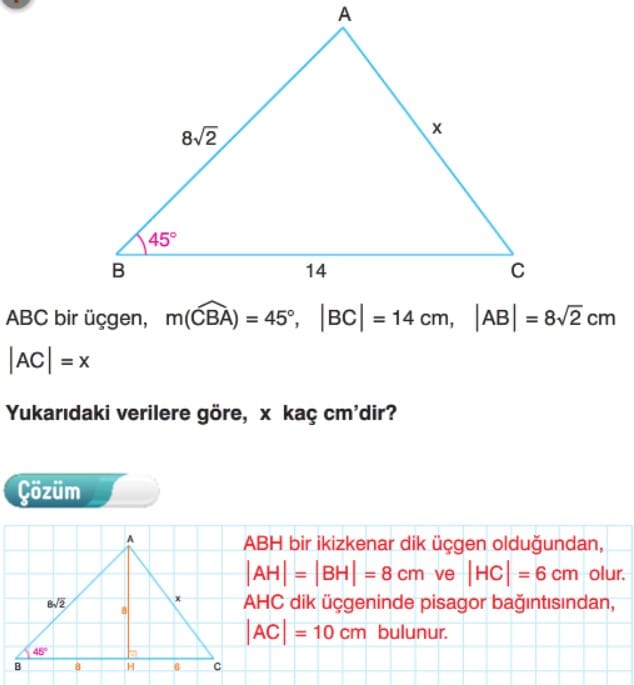
45-45-90 Dik Üçgeni

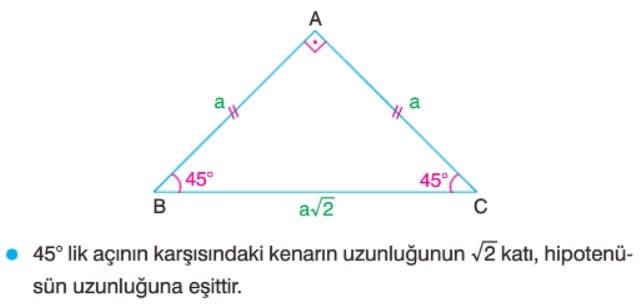
Çözümlü Sorular

---

Çözümlü Örnek Test Soruları

1. Soru
Bir dik üçgende dik kenarların uzunlukları 3 cm ve 4 cm’dir. Hipotenüsün uzunluğu nedir?
a) 5
b) 6
c) 7
d) 8
e) 9

Çözüm:
a kare + b kare = c kare
3 kare + 4 kare = c kare
9 + 16 = c kare
c kare = 25
c = 5
Cevap: a) 5

---

2. Soru
Bir dik üçgende hipotenüs uzunluğu 13 cm, bir dik kenarın uzunluğu 5 cm’dir. Diğer dik kenarın uzunluğu kaçtır?
a) 8
b) 9
c) 10
d) 11
e) 12

Çözüm:
a kare + b kare = c kare
5 kare + b kare = 13 kare
25 + b kare = 169
b kare = 169 – 25
b kare = 144
b = 12
Cevap: e) 12

---

3. Soru
Bir dik üçgende hipotenüs uzunluğu 10 cm, bir dik kenarın uzunluğu 6 cm’dir. Diğer dik kenar kaç cm’dir?
a) 6
b) 7
c) 8
d) 9
e) 10

Çözüm:
a kare + b kare = c kare
6 kare + b kare = 10 kare
36 + b kare = 100
b kare = 100 – 36
b kare = 64
b = 8
Cevap: c) 8

---

4. Soru
Bir dik üçgende dik kenarların uzunlukları 9 cm ve 12 cm’dir. Hipotenüs uzunluğu kaç cm’dir?
a) 13
b) 14
c) 15
d) 16
e) 17

Çözüm:
a kare + b kare = c kare
9 kare + 12 kare = c kare
81 + 144 = c kare
c kare = 225
c = 15
Cevap: c) 15

---

5. Soru
Bir dik üçgende hipotenüs uzunluğu 25 cm, bir dik kenarın uzunluğu 7 cm’dir. Diğer dik kenarın uzunluğu kaç cm’dir?
a) 20
b) 21
c) 22
d) 23
e) 24

Çözüm:
a kare + b kare = c kare
7 kare + b kare = 25 kare
49 + b kare = 625
b kare = 625 – 49
b kare = 576
b = 24
Cevap: e) 24

---

6. Soru
Bir dik üçgende dik kenarların uzunlukları 8 cm ve 15 cm’dir. Hipotenüs uzunluğu kaç cm’dir?
a) 16
b) 17
c) 18
d) 19
e) 20

Çözüm:
a kare + b kare = c kare
8 kare + 15 kare = c kare
64 + 225 = c kare
c kare = 289
c = 17
Cevap: b) 17

---

7. Soru
Bir dik üçgende hipotenüs uzunluğu 20 cm, bir dik kenarın uzunluğu 12 cm’dir. Diğer dik kenarın uzunluğu kaç cm’dir?
a) 12
b) 13
c) 14
d) 15
e) 16

Çözüm:
a kare + b kare = c kare
12 kare + b kare = 20 kare
144 + b kare = 400
b kare = 400 – 144
b kare = 256
b = 16
Cevap: e) 16

---

8. Soru
Bir dik üçgende hipotenüs 17 cm, bir dik kenar 8 cm’dir. Diğer dik kenar kaç cm’dir?
a) 10
b) 12
c) 14
d) 15
e) 16

Çözüm:
a kare + b kare = c kare
8 kare + b kare = 17 kare
64 + b kare = 289
b kare = 289 – 64
b kare = 225
b = 15
Cevap: d) 15