Dik Üçgende Dar Açıların Trigonometrik Oranları 9. Sınıf
Dik üçgenin kenar uzunluklarının birbirine oranlanmasına (bölünmesine) trigonometri denir.
Benzerliğin farklı bir uygulaması olarak düşünülebilir.
Çünkü, bir üçgenin iki kenar uzunluğunun birbirine oranı k ise bu üçgeni istediğimiz kadar büyüttüğümüzde yahut küçülttüğümüzde bu kenarların oranı yine k olur.
Bu sabit k oranına, trigonometrik oran diyoruz.
Trigonometrik oranlar aşağıdaki gibi standart hale getirilmiş ve sinüs, kosinüs, tanjant, kotanjant olarak isimlendirilmiştir.
Örnek:

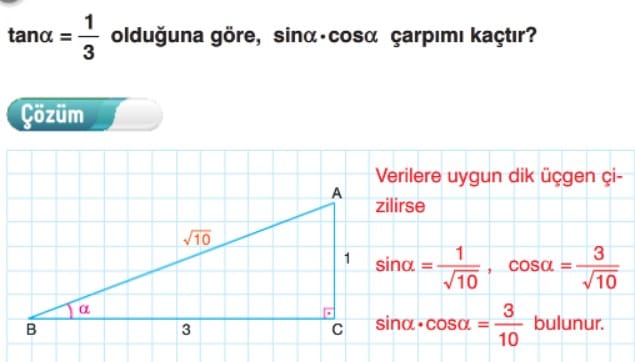
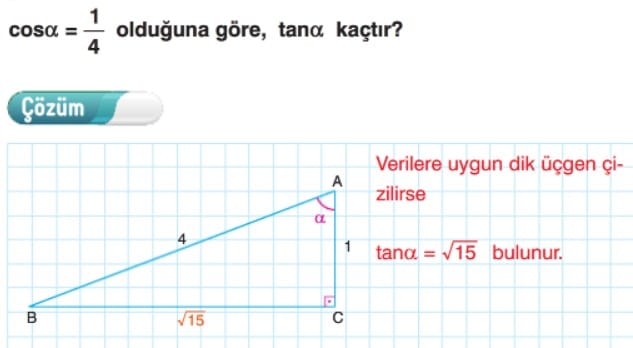
? Trigonometrik değerlerinden biri bilinen bir açının, diğer trigonometrik değerlerini bulabilmek için, mevcut verilere uygun bir dik üçgen çizilir.
Örnek:

Örnek:

Örnek:

Örnek:

Birim Çemberde Trigonometrik Oranlar
? Yarıçapı 1 birim olan çembere birim çember denir.
? Bu bölümde trigonometriyi, merkezi orijin olan birim çember üzerinde inceleyeceğiz.
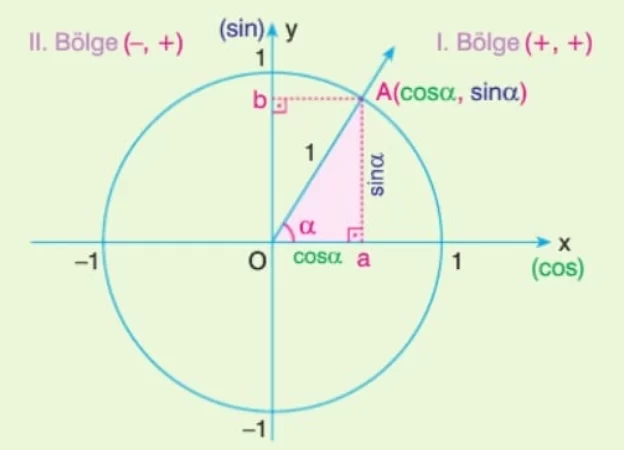
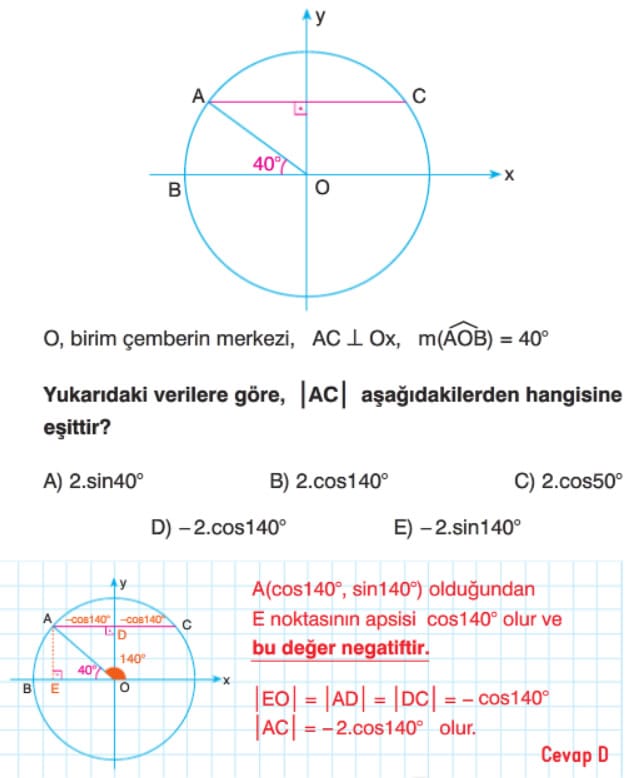
? Pozitif yönlü, başlangıç noktası orijin ve ölçüsü α olan bir açının birim çemberi kestiği A noktasının koordinatları (a, b) olsun.

? Dolayısıyla A noktasının apsisi cosα, ordinatı da sinα olur.
Örnek:

Dik Üçgende Dar Açıların Trigonometrik Oranları Çözümlü Sorular
Çözümlü Örnek Test Soruları
Konu: Dik Üçgende Dar Açıların Trigonometrik Oranları
1. Bir dik üçgende, ABC üçgeninde |AC| = 6, |BC| = 8 ve |AB| hipotenüstür. sin A değeri nedir?
A) 3/5
B) 4/5
C) 3/4
D) 5/6
Çözüm:
Öncelikle hipotenüsü bulalım:
AB² = AC² + BC²
AB² = 6² + 8²
AB² = 36 + 64 = 100
AB = 10
sin A = karşı / hipotenüs = 6 / 10 = 3/5
Doğru cevap: A
2. ABC dik üçgeninde, |AB| = 5 ve |AC| = 3 ise cos B nedir?
A) 3/5
B) 4/5
C) 5/3
D) 1/2
Çözüm:
Hipotenüsü bulalım:
BC² = AB² – AC²
BC² = 5² – 3²
BC² = 25 – 9 = 16
BC = 4
cos B = komşu / hipotenüs = 4 / 5
Doğru cevap: B
3. |AB| = 12 ve |AC| = 5 olan ABC dik üçgeninde tan A değeri kaçtır?
A) 5/12
B) 12/5
C) 5/13
D) 12/13
Çözüm:
Hipotenüsü bulalım:
BC² = AB² – AC²
BC² = 12² – 5²
BC² = 144 – 25 = 119
BC = √119
tan A = karşı / komşu = 5 / √119
Doğru cevap: A
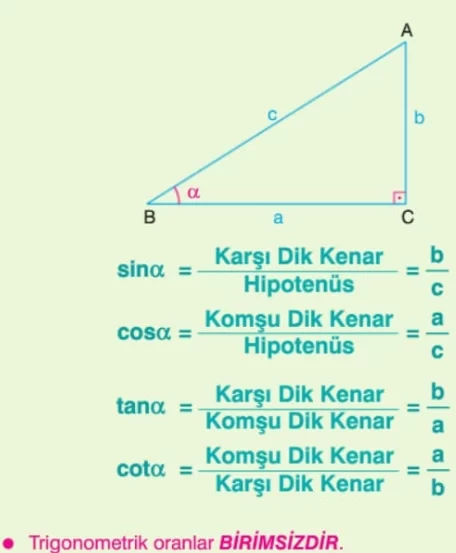
Dik üçgenin, bir dar açısına komşu olan dik kenar, karşısındaki dik kenar ve hipotenüs uzunluklarının birbirine oranları bazı özel adlar ile tanımlanmıştır. Tanımlanan bu oranlara trigonometrik oranlar denir. Bu oranlar, açının sinüsü (sin), kosinüsü (cos), tanjantı (tan) ve kotanjantı (cat) diye adlandırılır. Bu oranların tanımını bilmemiz gerekir.
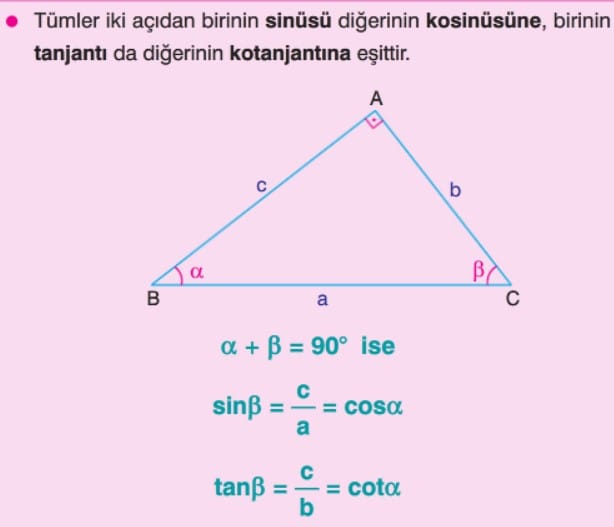
Ölçüleri toplamı 90° olan açılara tümler açılar denir. Tümler iki açıdan birinin sinüsü, diğerinin kosinüsüne, birinin tanjantı, diğerinin kotanjantına eşittir.
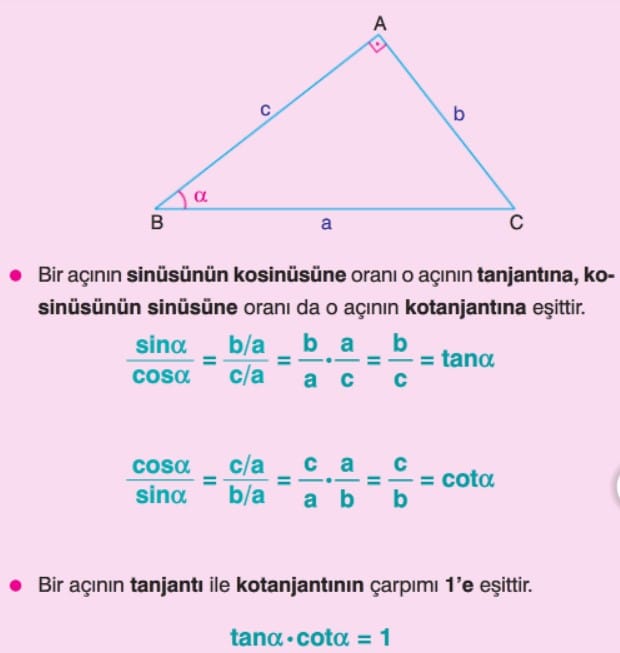
Bir dik üçgende, alfa bir dar açının ölçüsü ise sinüs alfa karşı dik kenar uzunluğu bölü hipotenüs uzunluğu, kosinüs alfa komşu dik kenar uzunluğu bölü hipotenüs uzunluğudur. Bir dik üçgende, alfa bir dar açının ölçüsü ise tanjant alfa karşı dik kenar uzunluğu bölü komşu dik kenar uzunluğu, kosinüs alfa komşu dik kenar uzunluğu bölü karşı dik kenar uzunluğudur.
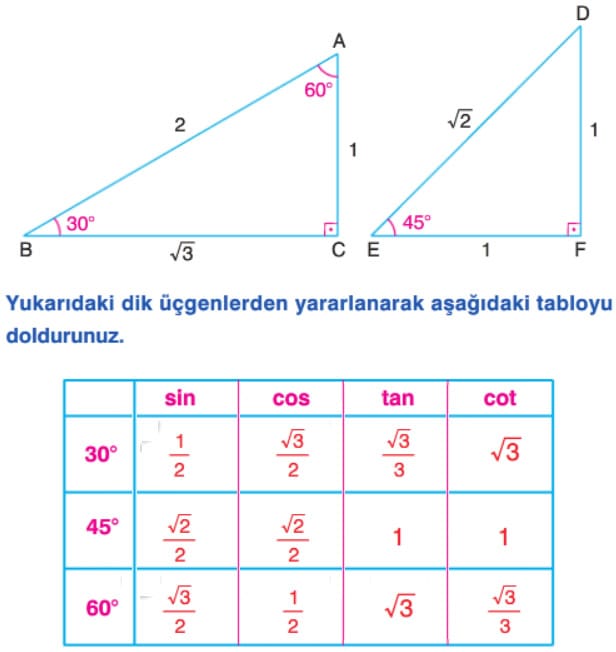
kenar uzunluğu 2 birim olan ABC eşkenar üçgeninde, AH yüksekliğini çizersek 30 60 90 dik üçgenini elde ederiz. Bu üçgen yardımıyla 30 ve 60 derecelik açıların sinüs kosinüs tanjant ve kotanjant oranlarını bulabiliriz.
Dik kenar uzunlukları 1 birim olan ABC ikizkenar dik üçgeni yardımıyla (45 45 90 dik üçgeni) 45 derecenin trigonometrik oranlarını yazabiliriz.
Dik üçgen, bir açısı tam olarak 90 derece olan üçgendir. Bu üçgende, dik açıya komşu olan diğer iki açı, sırasıyla, dik açıyı karşılık gelen kenarlarını hipotenüs ve dikey kenar olarak adlandırırız. Trigonometrik oranlar, bu dik üçgenin açıları ve kenarları arasındaki ilişkileri ifade eden matematiksel oranlardır. İşte dik üçgende trigonometrik oranlar:
Sinüs (sin): Bir açının sinüsü, o açının karşılık gelen kenarıyla hipotenüs arasındaki orandır. Mathematically,
sin(θ) = Karşı Dik Kenar / Hipotenüs
Kosinüs (cos): Bir açının kosinüsü, o açının hipotenüse olan dik uzaklığıyla hipotenüs arasındaki orandır. Mathematically,
cos(θ) = Komşu Dik Kenar / Hipotenüs
Tanjant (tan): Bir açının tanjantı, o açının karşılık gelen kenarı ile hipotenüs arasındaki orandır. Mathematically,
tan(θ) = Karşı Dik Kenar / Komşu Dik Kenar
Bu oranlar, dik üçgenin açılarını ve kenarlarını birbirine bağlayan temel trigonometrik fonksiyonlardır. Bu trigonometrik oranlar, özellikle trigonometri alanında kullanılan temel kavramlardır ve birçok matematiksel problemin çözümünde önemli bir role sahiptirler.
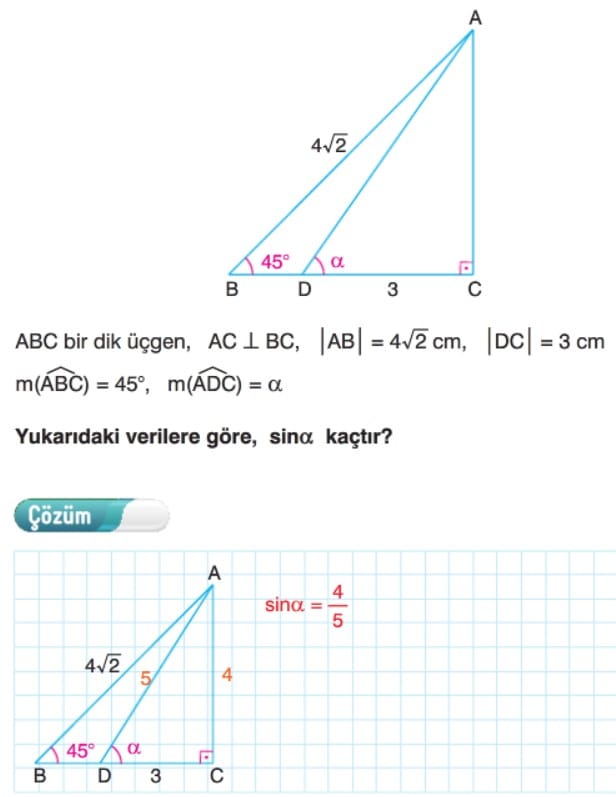
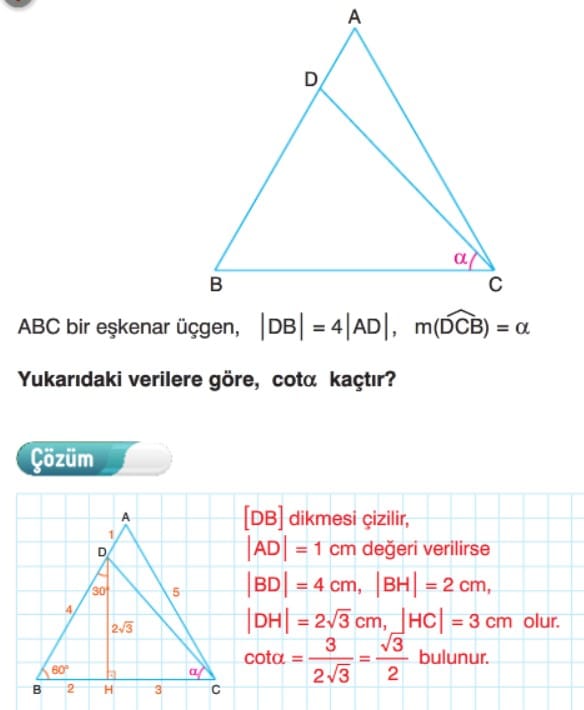
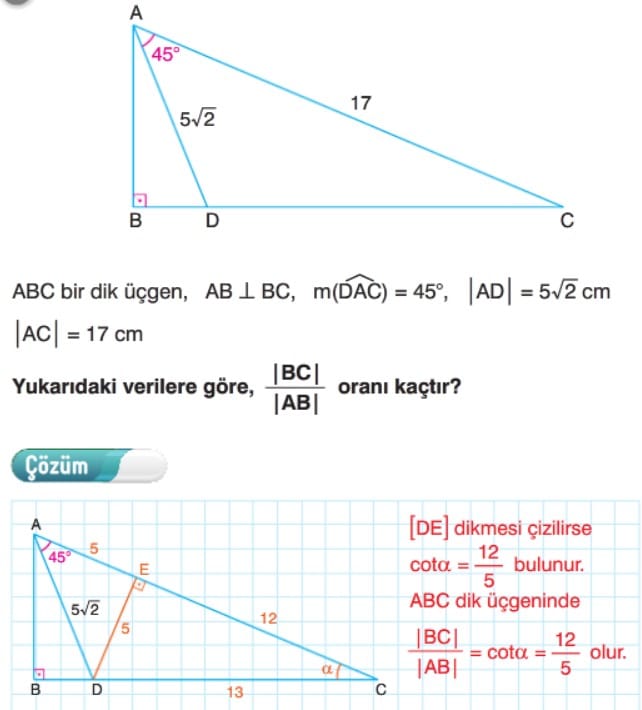





Sayenizde tamamlayamadığım notlarımı tamamlayarak çalışıyorum ancak birim çember konusu da ekler misiniz ? teşekkürler.