Dik Dairesel Silindir 11. Sınıf Matematik
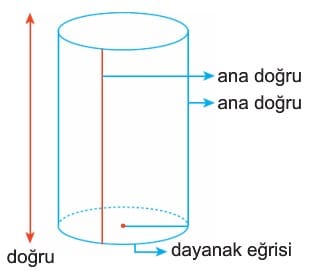
Düzlemsel bir eğriyle bu eğrinin düzleminde bulunmayan bir doğru verildiğinde daima bu doğruya paralel kalmak koşuluyla eğriye dayanarak hareket eden bir doğrunun taradığı yüzeye silindirik yüzey denir. Silindirik yüzeyle bu yüzeyi kesen iki düzlemin sınırladığı cisme silindir denir. Silindir yüzeyini oluşturan doğruların her birine ana doğru denir.

Dik Dairesel Silindir veya Dönel Silindir
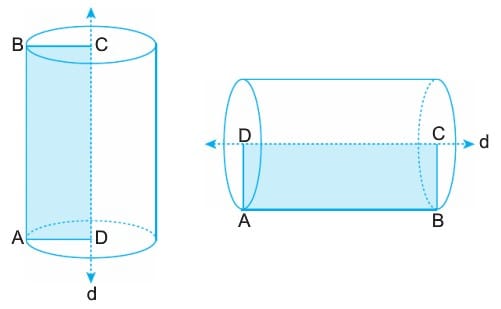
Yukarıdaki silindirler ABCD dikdörtgeninin [CD] etrafında 360° döndürülmesiyle elde edilmiştir.
Dik Dairesel Silindirin Alanı
Yukarıdaki dik dairesel silindir ana doğrusu boyunca kesilerek düzleme açıldığında
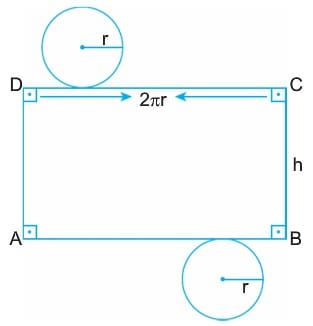
Şekli elde edilir. Burada ABCD bir dikdörtgendir.
|AB| = 2 . π . r (Çemberin çevresi)
- Yanal Alan:
A(ABCD) = 2πr . h - Yüzey (bütün) Alan:
A(ABCD) + 2 Dairenin alanı
Alan = 2πr . h + 2πr2
Dik Dairesel Silindirin Hacmi
Silindirin tabanı daire olduğundan dairenin alanı πr2 dir.
Hacim (silindir) = πr2 . h br3
Çözümlü Sorular
Dik Dairesel Silindir Video Hocalara Geldik
Dik Dairesel Silindir Video Yarıçap Yayınları
Çözümlü Örnek Test Soruları
1. Soru:
Taban yarıçapı 3 cm, yüksekliği 8 cm olan dik dairesel silindirin hacmi kaç cm küptür? (π = 3 alınacaktır.)
A) 216
B) 72
C) 144
D) 192
Cevap: A
Çözüm:
Dik dairesel silindirin hacmi formülü V = π.r².h
Burada π = 3, r = 3 cm ve h = 8 cm olduğundan:
V = 3 × 3² × 8 = 3 × 9 × 8 = 216 cm küptür.
2. Soru:
Taban çevresi 10π cm ve yüksekliği 12 cm olan dik dairesel silindirin yanal yüzey alanı kaç cm karedir?
A) 100π
B) 120π
C) 200π
D) 240π
Cevap: B
Çözüm:
Silindirin yanal yüzey alanı = 2πr × h (taban çevresi × yükseklik)
Taban çevresi = 2πr = 10π → r = 5 cm
Yanal Alan = 10π × 12 = 120π cm² olur.
3. Soru:
Hacmi 300π cm³ olan dik dairesel silindirin taban yarıçapı 5 cm olduğuna göre yüksekliği kaç cm’dir?
A) 6
B) 10
C) 12
D) 15
Cevap: C
Çözüm:
V = πr²h
300π = π × 5² × h → 300π = π × 25 × h
300π ÷ 25π = h → h = 12 cm bulunur.
4. Soru:
Yüksekliği taban yarıçapının iki katı olan bir dik dairesel silindirin hacmi 128π cm³ olduğuna göre taban yarıçapı kaç cm’dir?
A) 2
B) 4
C) 6
D) 8
Cevap: B
Çözüm:
Yükseklik h = 2r,
Hacim formülü: πr²h = 128π
πr² × 2r = 128π
2πr³ = 128π → r³ = 64 → r = 4 cm olur.
5. Soru:
Bir dik dairesel silindirin taban yarıçapı 7 cm ve yüksekliği 20 cm’dir. Bu silindirin tüm yüzey alanı kaç π cm²’dir?
A) 378
B) 196
C) 270
D) 450
Cevap: A
Çözüm:
Tüm yüzey alanı formülü: 2πr(h + r)
= 2π × 7 (20 + 7)
= 14π × 27
= 378π cm² olur.
Yanal ayrıtları tabanlara dik olan prizmaya dik prizma denir. Prizmalar tabanlarındaki geometrik şekle göre adlandırılır. Aşağıdaki cisim üçgen dik prizmadır.
Dik prizmanın taban çevresi TÇ ve yüksekliği h ise yanal alanı YA = TÇ . h olur. Bir dik prizmanın taban alanı TA ve yanal alanı YA olmak üzere yüzey alanı A = 2 TA + YA ve hacmi V = TA. h bağıntısıyla bulunur.
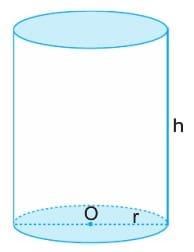
Yandaki şekilde silindiri oluşturan düzlemler arasında kalan dikme parçasına silindirin yüksekliği (h), silindirin altında ve üstünde oluşan kesitlere alt ve üst taban yüzeyleri, silindirik yüzey parçasına silindirin yanal yüzeyi, taban yüzeylerinin merkezlerini birleştiren doğruya da silindirin ekseni adı verilir. Tabanları karşılıklı iki noktasını birleştiren ve eksene paralel olan doğrulara ise dairesel silindirin ana doğruları denir. Ana doğruları dayanak eğrisinin bulunduğu düzleme dik olan silindire dik silindir denir. Alt ve üst tabanları daire olan dik silindir, dik dairesel silindir olarak adlandırılır.
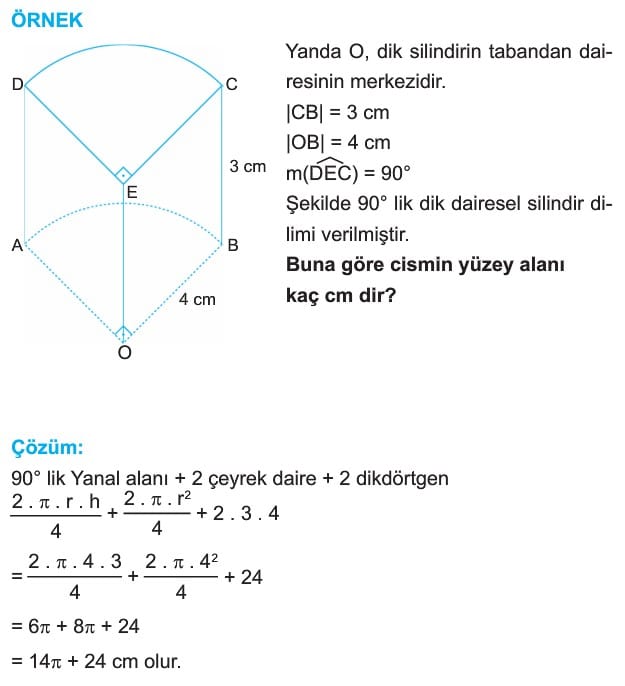
ÖRNEK: Taban yarıçapı 3 cm, yüksekliği 4 cm olan silindirin yanal ve tüm alanı kaç cm2 dir.
Çözüm: Yanal Alan (Sy) = 2πr . h
= 2.π.3.4 = 24πcm2
Tüm Alan (S)=2πr.h+2πr2
= 2.π.3.4 + 2π32
=24π+18π
=42πcm2
ÖRNEK: Hacimi 45π cm3 olan dik silindirin yüksekliği 5 cm olduğuna göre, taban yarıçapı kaç cm olur?
Çözüm: Vs = πr2 . h = 45π
πr2 . 5 = 45π
r2 = 9 ise r = 3 cmdir.
ÖRNEK: Taban yarıçapı 3 cm, yüksekliği 4 cm olan silindirin yanal ve tüm alanı kaç cm2 dir.
Çözüm: Yanal Alan (Sy) = 2πr . h
= 2.π.3.4 = 24πcm2
Tüm Alan (S)=2πr.h+2πr2
= 2.π.3.4 + 2π32
=24π+18π
=42πcm2
ÖRNEK: Yandaki dik silindirin taban yarıçapı 3, yüksekliği 5 cm dir. Üstü açık bu silindirin iç ve dış yüzeyleri boyanmıştır. Buna göre, boyanmış yüzeyin alanı kaç santimetre karedir?
Çözüm: Hem iç hemde dış yüzeyi boyandığından
Boyalı kısım = 2 . alt taban alanı + 2 . yanal alan
= 2πr2 + 2πrh
= 2π32 + 2π3.5
= 18π + 60π
= 78π cm2 olur.
Soru: Yanda yer düzlemine dik duran içi dolu silindir şeklindeki bir tahta parçası tabana dik bir biçimde kesilerek düzlemsel bir bölge elde ediliyor. Buna göre elde edilen bu düzlemsel bölge aşağıdakilerden hangisi olur?
A) Üçgensel bölge
B) Dairesel bölge
C) Dikdörtgensel bölge
D) Altıgensel bölge
E) Beşgensel bölge
Soru: Karesel bir karton kıvrılarak taban dairesinin yarıçapı 4 cm olan bir dik silindir oluşturuluyor. Buna göre, bu silindirin hacmi kaç pi cm3 tür?
A) 100 B) 112 C) 125 D) 135 E) 144
Alıştırma: Aşağıdaki boşlukları tablodaki uygun ifadelerle doldurunuz.
1. Taban yarıçapı 3 cm yüksekliği 2 cm olan dik dairesel silindirin hacmi …………………………. cm3 tür.
2. Hacmi 751: cm3 ve yüksekliği 3 cm olan dik dairesel silindirin taban yarıçapı …………………………. cm dir.
3. Bir dik dairesel silindirin yüksekliği 4 cm yanal alanı 481: cm2 ise taban yarıçapı …………………………. cm dir.
4. Taban yarıçapı yüksekliğine eşit dik dairesel silindirin hacmi Bir cm3 ise taban yarıçapı …………………………. cm dir.
5. Hacmi ve yanal alanı eşit olan dik dairesel silindirin taban çapı …………………………. br dir.