Deneysel ve Teorik Olasılık 11. Sınıf
Olasılık çeşitleri Teorik, Deneysel ve Öznel olasılık olmak üzere 3 çeşittir.
1. Deneysel Olasılık
Olasılık değerlerinin deneyerek, yaparak hesaplandığı olasılık türüdür.
Deneysel Olasılık Soruları ve Çözümleri
2. Teorik Olasılık
Deney yapmadan olasılık sonucunun hesaplanarak bulunduğu olasılık çeşitidir.
BİLGİ: Deneysel olasılıktaki deneme sayısı arttırıldığında sonucun teorik olasılığa yaklaştığı görülür.
3. Öznel Olasılık
Kişilerin kendi düşüncelerine göre karar verdikleri olasılıklara denir. Bu şekildeki olasılıklarda kişinin tahmini ve ismi yer alır.
Örneğin;
Galatasaray – Beşiktaş maçının sonucuna yönelik tahminler şöyledir.
Sedat: %70 Galatasaray kazanır.
Gürkan: %90 Beşiktaş kazanır.
İsmet: %100 Berabere kalırlar.
Bu olasılık tahminleri kişiden kişiye değiştiğinden dolayı öznel olasılıktır.
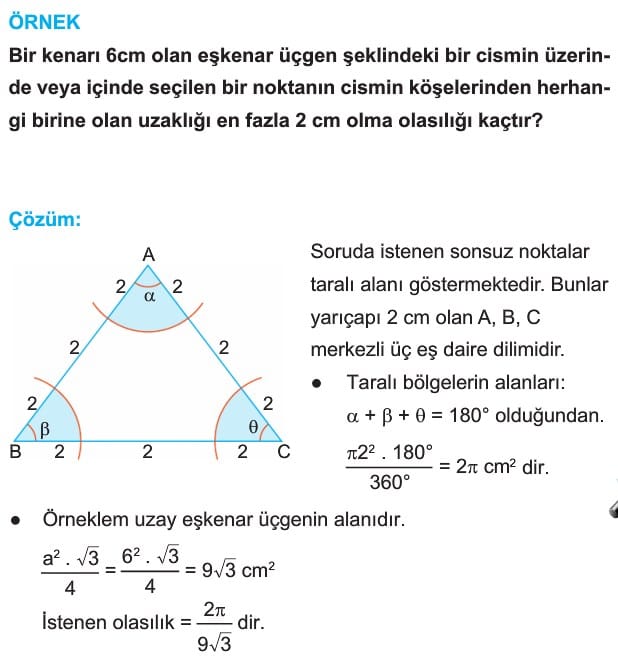
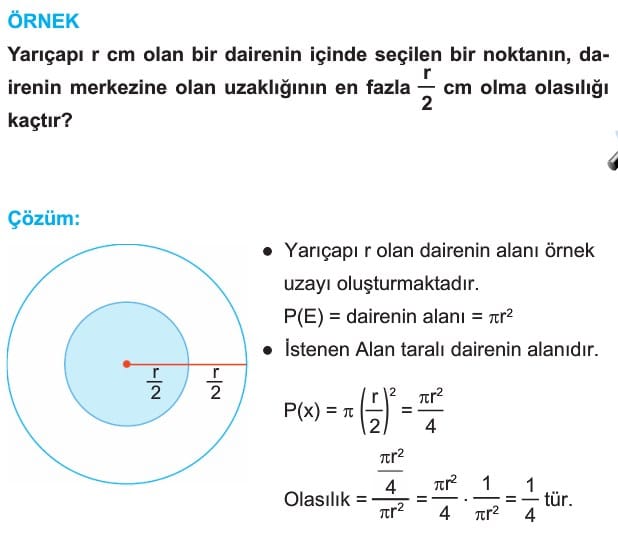
Sonsuz Elemanlı Örneklem Uzayında Olasılık
E örneklem uzayı sayılamayacak çoklukta örnek noktalardan (uzunluk, açı, alan, birim, …,) oluşuyorsa bu örneklem uzayına sonsuz örneklem uzayı denir.
x olayı E örneklem uzayında bir olay ise x in olasılığı
Sonsuz Elemanlı Örneklem Uzayında Olasılık Soruları ve Çözümleri
Deneysel ve Teorik Olasılık konu anlatımı soruları çözümleri 11. Sınıf
Örneğin; Damla hilesiz bir zarın 4 gelme olasılığını hesaplamak istiyor. Zarı 100 kez atıyor 83 kez 4 geliyor. Bulunan olasılık 83/100 dür. Zarı 500 kez atıyor 281 kez 4 geliyor. Bulunan olasılık 281/500 dür. Damla bu olasılıkları deneyerek bulmuştur. Bulunan bu olasılık deneysel olasılıktır.
Soru: Ege'nin üniversite sınavını kazanma olasılığı x, Eylül'ün üniversite sınavını kazanma olasılığı y dir. Buna göre, sadece birinin üniversite sınavını kazanma olasılığı hangisidir?
A) x+y-xy B) (x+1)(y-1) C) x+y
D) x+y-2xy E) (x+1)(y+1)
Soru: 30 kişilik bir sınıfta 10 öğrenci futbol, 15 öğrenci basketbol, 4 öğrenci her iki oyunu da oynamaktadır. Bu sınıftan seçilen bir öğrencinin futbol oynamadığı bilindiğine göre basketbol oynuyor olma olasılığı kaçtır?
Soru: Bir köydeki ailelerin %50 sinin televizyonu, %30 unun bulaşık makinesi %10 ununda hem televizyonu hem de bulaşık makinesi vardır. Bu köyden rastgele seçilen bir ailenin bulaşık makinesi yoksa televizyonlarının olma olasılığı kaçtır?
Soru: Bir torbada 4 kırmızı 5 siyah top vardır. Bu torbadan arka arkaya alınan iki topun birincisinin kırmızı ikincisinin siyah top olma olasılığı kaçtır?
Soru: Birinci torbada 4 kırmızı 5 siyah, ikinci torbada 3 kırmızı 2 siyah top vardır. 2. torbadan bir top alınıp 1. torbaya atılıyor. Bu durum sonrasında 1. torbadan alınan bir topun siyah renkli olma olasılığı kaçtır?
Soru: Bir sınıfta 10 kız 12 erkek öğrenci vardır. Bu sınıftaki kızların 3 ü erkeklerin 5 i beşiktaşlıdır. Bu sınıftan seçilen bir öğrencinin erkek veya beşiktaşlı olma olasılığı kaçtır?
Soru: 6 erkek 4 kızdan oluşan 10 kişilik bir gruptan 3 kişilik bir komite oluşturulacaktır. Bu komitede en az 2 erkek bulunma olasılığı kaçtır?
Soru: Bir sınıftaki öğrencilerin %40 ı erkektir. Erkeklerin %40 ı kızların %6O ı sınıflarını teşekkür belgesi alarak geçmişlerdir. Rastgele seçilen bir öğrencinin teşekkür belgesi aldığı bilindiğine göre kız öğrenci olma olasılığı kaçtır?
Soru: Bir sınıftaki öğrencilerin %40 ı fizik, %50 si matematik, %10 u da hem fizik hem de matematik dersinden proje almışlardır. Bu sınıftan rastgele seçilen bir öğrencinin matematikten proje almadığı bilindiğine göre fizikten de proje almış olma olasılığı kaçtır?
Soru: Birinci torbada 5 yeşil 4 sarı; ikinci bir torbada 3 yeşil 2 sarı 4 bilye vardır. Birinci torbadan bir bilye çekilip ikinci torbaya atılıyor. Daha sonra ikinci torbadan bir bilye çekilip birinci torbaya atılıyor. Bu durumdan sonra torbalardaki bilyelerin ilk durumla aynı olma olasılığı kaçtır?
Soru: İki torbadan birincisinde 3 mavi, 4 sarı; ikincisinde ise 2 mavi 5 sarı top vardır. Bir madeni para atılıyor. Para tura geldiğinde 1. torbadan, para yazı geldiğinde 2. torbadan bir top çekiliyor. Buna göre, çekilen topun sarı renkli olma olasılığı kaçtır?
Soru: Bir atölyede üretilen ürünlerin %60 ı X makinesinde, %40 ı Y makinesinde üretilmektedir. Bu makinelerdeki arızalı üretim oranları
X için %5
Y için %10
olduğuna göre, rastgele alınan bir ürünün bozuk veya Y makinesinde üretilmiş olma olasılığı yüzde kaçtır?
Uygulama: Bir şirket Bursa’da ilk kurduğu fabrikada televizyonlar için uzaktan kumanda üretmektedir. Talebin çok olması üzerine şirket yetkilileri girişimcilik örneği göstererek ve farklı bölgelerdeki hizmeti daha kolay karşılamak adına İzmir ile Malatya illerinde daha büyük kapasiteli birer tane fabrika kurar. Malatya’da günde 500, İzmir’de günde 450 ve Bursa’da günde 300 adet olmak üzere günde toplam 1250 adet uzaktan kumanda üretilmektedir. Üretilen uzaktan kumandaların Malatya’da %5 i, İzmir’de %6 sı, Bursa’da %2 si bozuk çıkmaktadır. Gün sonunda üretilen uzaktan kumandalardan rastgele seçilen birinin
a. Bozuk çıkma olasılığı,
b. Sağlam çıkma olasılığı,
c. Bozuk çıktıysa Malatya’da üretilmiş olma olasılığı,
ç. Sağlam çıktıysa İzmir’de üretilmiş olma olasılığını bulalım.
Tanıyalım: Şans oyunlarının bol olduğu Grek ve Roma toplumlarında yaşamış matematikçiler arasında Thales (Tales), Pyhagoras (Pisagor), Eulides (Öklit), Apollonius ve Archimedes gibi matematikçiler vardır. Oysa bu matematikçilerden kalan çalışmalarda olasılık kuramıyla ilgili tek bir ize dahi rastlanmamaktadır. Bugün olasılık kavramının başlangıcı olarak bilinen 1654 yılında neler olup bittiği enine boyuna bilinmektedir (Korkmaz, 2005). Chevalier de Méré, oyun yaşamındaki deneyimlerinden türettiği iki soruyu (biri zar sorusu, diğeri de bölüştürme sorusu) Blaise Pascal’a (1623 - 1662) yöneltmiş ve o da bu soruları çözmüştür. Fakat o dönemin büyük matematikçilerinden biri olarak kabul edilen Gilles Persone de Roberval’in eleştirileriyle karşılaşınca (Hacking, 1975, s. 125 aktaran Korkmaz, 2005) yaptıklarından kuşkulanmış, bu kuşkuları kafasından atabilmek için de yine o dönemin en büyük matematikçisi olarak kabul edilen Pierre de Fermat ile yazışmaya başlamıştır. İşte olasılık kuramı bu yazışmalardan doğmuştur. (Gillies, 2000, s. 3 aktaran Korkmaz, 2005).
Şans kavramını matematiğe Pascal ve Fermat kazandırmıştır fakat olasılığın kurucusu olarak Laplace bilinir. Bugünkü anlamda gelişimini Poisson’un (1781 - 1840) çalışmalarına borçludur. İlk dönemlerde bir olayın olma olasılığının gözlenmesiyle teorik olarak olma olasılığının bazı durumlarda örtüşmemesi nedeniyle zaman zaman olasılık ilkelerine şüpheyle bakılmıştır. Pascal ve Poisson bu sorunlu durumu çözmek için önemli çalışmalar yapmışlardır. Olasılıktaki kapsamlı gelişmeler Kolmogorov (1903 - 1987) tarafından 1930 yılında yazılan “Olasılık Kavramının Temelleri” kitabı ile başlamıştır. Artık Kolmogorov ile birlikte olasılık aksiyomatik bir temele oturtulmuş olur. (Baki, 2014, s.159).