Deltoid ve Özellikleri, Deltoidin Alanı 10. Sınıf

10. sınıf Matematik Konuları Konu Anlatımları Matematik

02.04.2025

Tabanları çakışık olan iki ikizkenar üçgenin oluşturduğu dörtgene deltoid denir.

DELTOİDİN ÖZELLİKLERİ

Deltoidin eş olmayan kenarlarının oluşturduğu açılar eştir.

Bir deltoidde, eş kenarların ortak köşelerini birleştiren köşegen, bu köşelerdeki açıların açıortayıdır.

Bir deltoidde eş kenarların ortak köşelerini birleştiren köşegen, diğer köşegene diktir ve bu köşegeni ortalar.

Çözümlü Sorular

DELTOİDİN ALANI

Çözümlü Sorular

Deltoid ve Özellikleri Hocalara Geldik

Çözümlü Örnek Test Soruları

Soru 1:
Bir deltoidin kenar uzunlukları 5 cm, 5 cm, 7 cm ve 7 cm’dir. Bu deltoidin çevresi kaç cm’dir?
A) 24
B) 22
C) 20
D) 18

Çözüm: Deltoidin çevresi = 5 + 5 + 7 + 7 = 24 cm
Cevap: A

Soru 2:
Köşegen uzunlukları 10 cm ve 6 cm olan bir deltoidin alanı kaç cm²’dir?
A) 30
B) 60
C) 15
D) 45

Çözüm: Deltoidin alanı = (10 × 6)/2 = 30 cm²
Cevap: A

Soru 3:
Aşağıdaki ifadelerden hangisi deltoid için yanlıştır?
A) İki çift eşit kenarı vardır
B) Köşegenleri dik kesişir
C) Karşılıklı açıları eşittir
D) Köşegenlerinden biri simetri eksenidir

Çözüm: Deltoidde karşılıklı açılar eşit olmak zorunda değildir.
Cevap: C

Soru 4:
Bir deltoidin uzun köşegeni 12 cm’dir ve bu köşegen deltoidi 8 cm² alanlı iki üçgene ayırıyorsa, kısa köşegenin uzunluğu kaç cm’dir?
A) 4
B) 8/3
C) 16/3
D) 6

Çözüm:
Alan = (12 × kısa köşegen)/2 = 16 ⇒ kısa köşegen = 16/3 cm
Cevap: C

Soru 5:
Çevresi 32 cm olan bir deltoidin eşit kenarlarından biri 6 cm ise, diğer eşit kenar çiftinin uzunluğu kaç cm’dir?
A) 10
B) 8
C) 12
D) 14

Çözüm:
6 + 6 + x + x = 32 ⇒ 2x = 20 ⇒ x = 10 cm
Cevap: A

Deltoid Özellikleri:

İki çift eşit kenarı vardır
Köşegenleri dik kesişir
Köşegenlerinden biri simetri eksenidir
Alan = (Köşegenler çarpımı)/2
Çevre = 2 × (farklı kenar çiftlerinin toplamı)

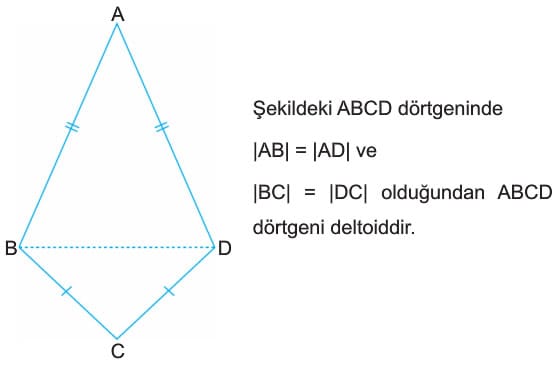
Şekildeki ABCD dörtğeninde |AB| = |AD| ve |BC| = |DC| olduğundan ABCD dörtgeni deltoiddir.
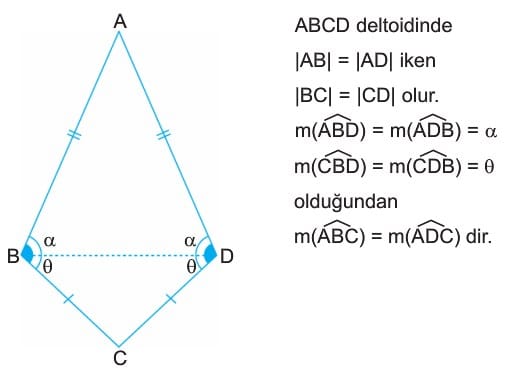
ABCD deltoidinde |AB| = |AD| iken |BC| = |CD| olur. m(ABD) = m(ADB) = alfa
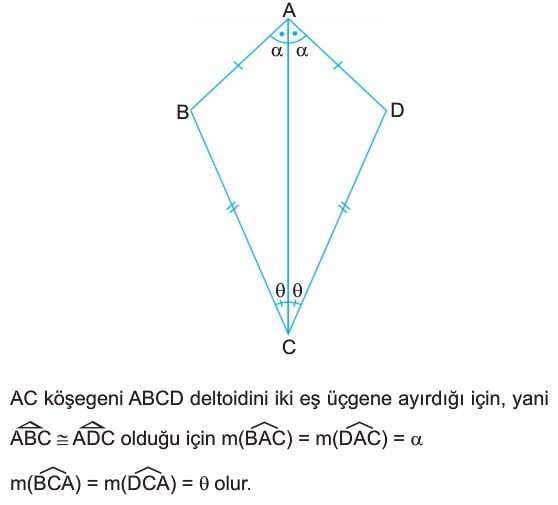
m(CBD) = m(CDB) = beta olduğundan m(ABC) = m(ADC)
AC köşegeni ABCD deltoidini iki eş üçgene ayırdığı için, yani
ABC eştir ADC üçgeni olduğu için m(BAC) = m(DAC) = alfa
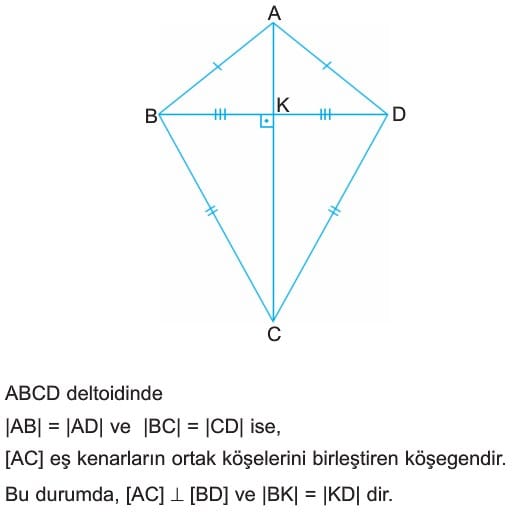
m(BCA) = m(DCA) = beta olur.
ABCD deltoidinde
|AB| = |AD| ve |BC| = |CD| ise,
[AC] eş kenarların ortak köşelerini birleştiren köşegendir.
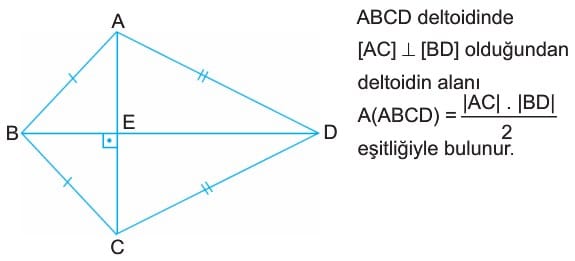
Bu durumda, [AC] dik [BD] ve |BK| = |KD| dir.
ABCD deltoidinde [AC] dik [BD] olduğundan deltoidin alanı
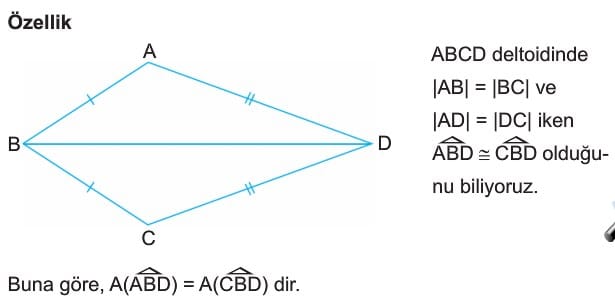
A(ABCD) = |AC| . |BD| / 2 eşitliğiyle bulunur.
Özellik: ABCD deltoidinde |AB| = |BC|, |AD| = |DC| iken ABD eştir CBD üçgeni olduğunu biliyoruz. Bundan dolayı A(ABD) = A(CBD) dir.
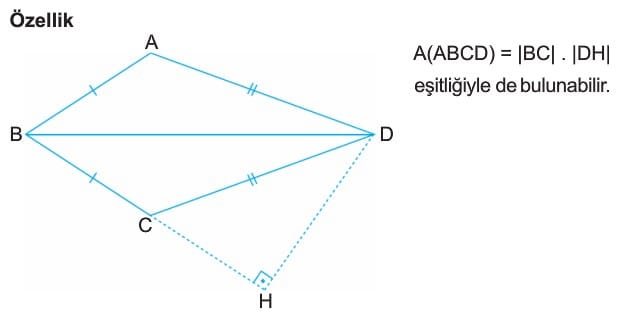
Özellik: ABCD deltoidinde D köşesinden karşı kenarın uzantısına yükseklik çizilerek, A(ABCD) = |BC| . |DH| eşitliğiyle de bulunabilir.

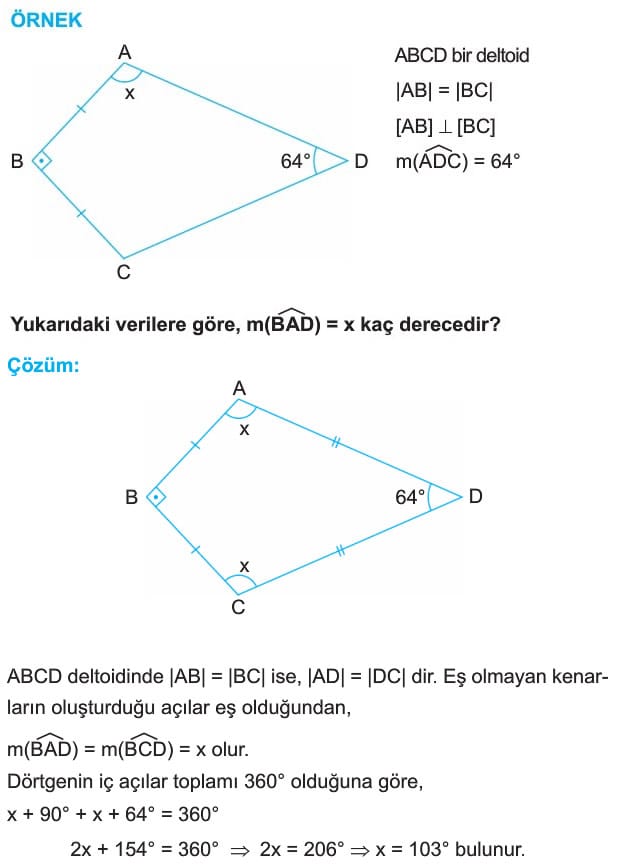
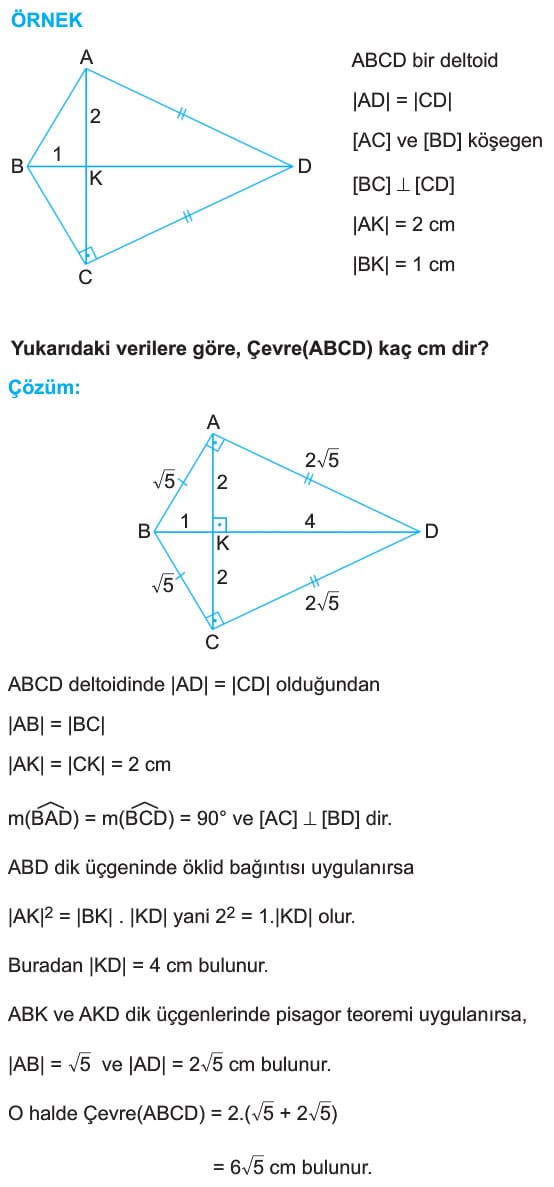
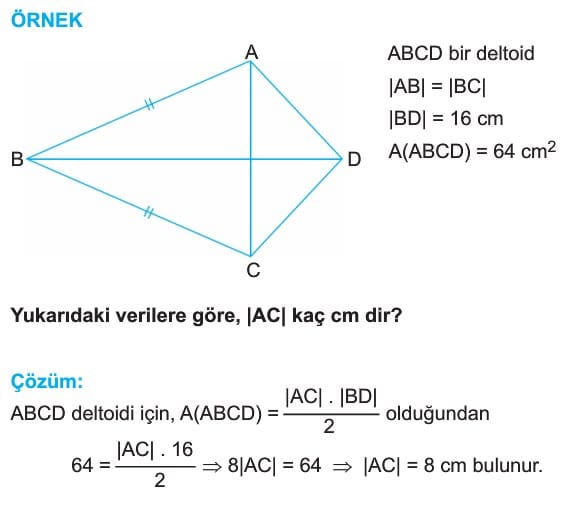
ÖRNEK: ABCD bir deltoid
|AB| = |BC|
[AB] dik [BC]
m(ADC) = 64°
Yukarıdaki verilere göre, m(BAD) = x kaç derecedir?
Çözüm: ABCD deltoidinde |AB| = |BC| ise, |AD| = |DC| dir. Eş olmayan kenarların oluşturduğu açılar eş olduğundan,
m(BAD) = m(BCD) = x olur.
Dörtğenin iç açılar toplamı 360° olduğuna göre,
x + 90° + x + 64° = 360°
2x + 154° = 360° ise 2x = 206° ise x =103° bulunur.

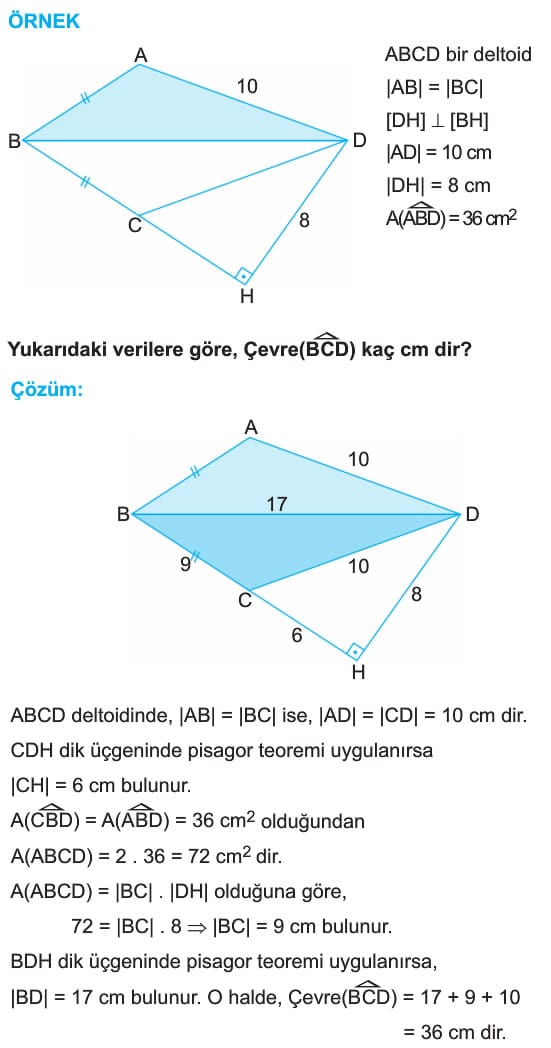
ÖRNEK: ABCD bir deltoid
|AB| = |BC|
[DH] dik [BH]
|AD| = 10 cm
|DH| = 8 cm
A(ABD)=36 cm²
Yukarıdaki verilere göre, Çevre(BCD) kaç cm dir?
Çözüm: ABCD deltoidinde, |AB| = |BC| ise, |AD| = |CD| = 10 cm dir.
CDH dik Üçğeninde pisagor teoremi uygulanırsa
|CH| = 6 cm bulunur.
A(CBD) = A(ABD) = 36 cm2 olduğundan
A(ABCD) = 2. 35 = 72 cm2 dir.
A(ABCD) = |BC| . |DH| olduğuna göre,
72 = |BC| . 8 ise |BC| = 9 cm bulunur.
BDH dik üçgeninde pisagor teoremi uygulanırsa,
|BD| = 17 cm bulunur. O halde, Çevre(BCD) = 17 + 9 +10 = 36 cm dir.

Deltoid konusu 11. sınıf geometri müfredatında yer almakta olup, ygs matematik, lys matematik ve kpss matematik sınavlarında soru gelebilmektedir. Geometri dersi Deltoid konu anlatımı videosu konu başlıkları,