n kenar sayısını göstermek Üzere n 2 3 olan kapalı şekillere çokgen denir.

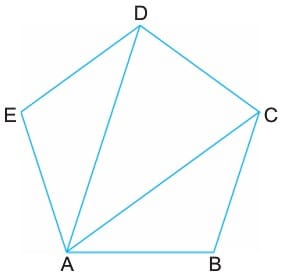
Şekildeki ABCDE çokgeninde A, B, C, D ve E noktalarına çokgenin köşeleri, [AB], [BC], [CD], [DE] ve [EA] doğru parçalarına çokgenin kenarları denir. Çokgenin içine çizilen [AD] ve [AC] doğru parçalarına çokgenin köşegenleri denir.

Çokgenler kenar sayısına göre isimlendirilir. Üç kenarlı ise Üçgen, dört kenarlı ise dörtgen isimini alır. ABCDE çokgeni beş kenarlı olduğundan beşgendir. Beşgenin 5 tane iç açısı, 5 tane de dış açısı vardır.

Kenar sayısı n olan bir çokgenin iç açılarının ölçüleri toplamı (n – 2). 180⁰ formülüyle bulunur.

Örneğin:
5 kenarlı bir çokgenin iç açılar toplamı (5 – 2).180° = 540°
6 kenaı1ı bir çokgenin iç açılar toplamı (6 – 2).180° = 720° ve
7 kenarlı bir çokgenin iç açılar toplamı (7 – 2).180° = 900° dir.

Dış açılar toplamı ise 360⁰ dir. Dış açılar toplamı kenar sayısına bağlı değildir.

Düzgün Çokgen

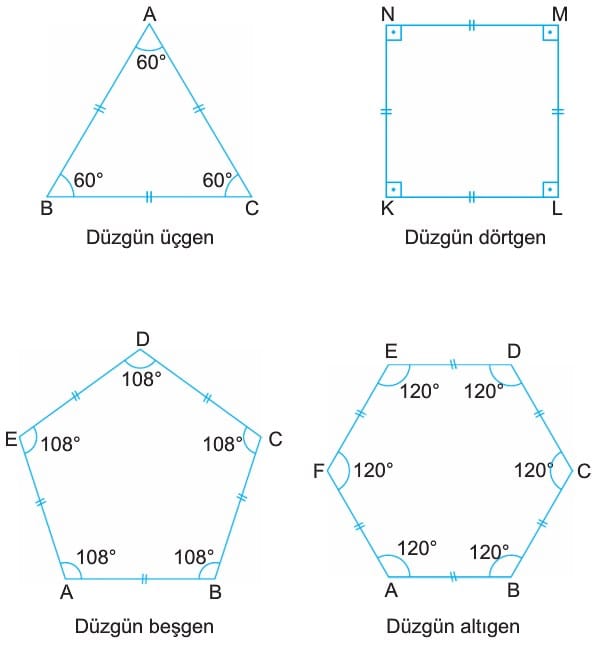
Tüm kenar uzunlukları, tüm iç açıları ve tüm dış açıları eşit olan çokgene düzgün çokgen denir. Eşkenar Üçgen, düzgün üçgen, kare ise düzgün dörtgendir.

2) Düzgün Çokgenlerin Özellikleri

1. Özellik

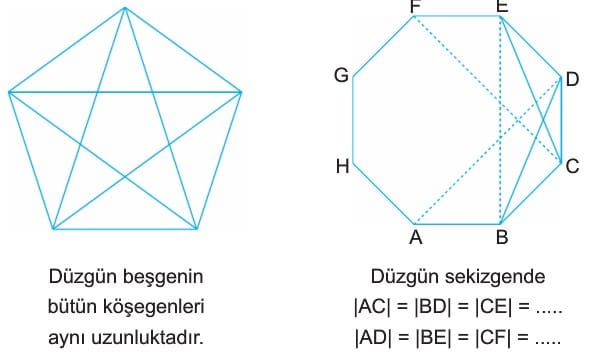
• Bir düzgün çokgende sabit bir köşeden aynı sayıda kenar atlanarak çizilen köşegenlerin uzunlukları eşittir.

2. Özellik

3. Özellik

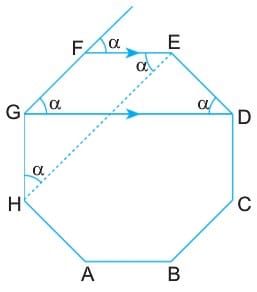
ABCDEFGH düzgün çokgeninde [GD] çizilerek GDEF dörtgeni, [HE] çizilerek HEFG dörtgeni oluşturulmuştur. Bu şekilde oluşturulan dörtgenler ikizkenar yamuktur. [FE] // [GD] ve [HE] // [GF] dir.

4. Özellik

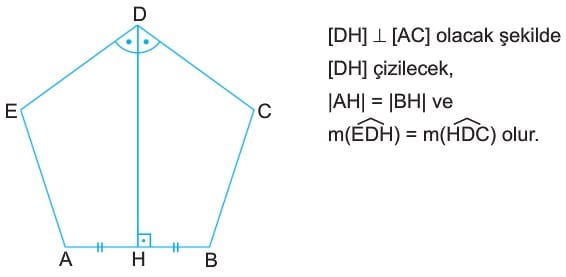
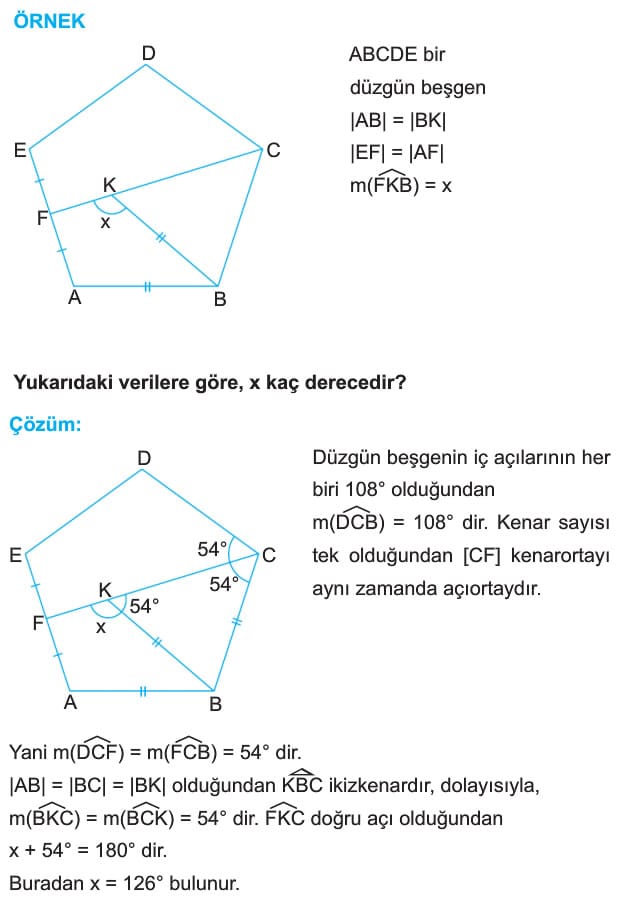
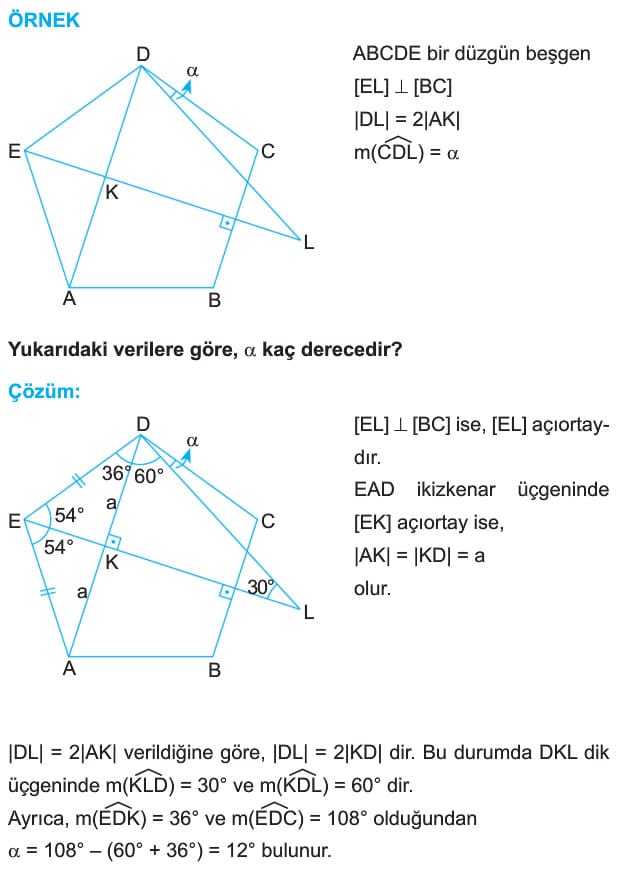
Bir düzgün çokgende kenar sayısı tek ise, bir köşeden karşısındaki kenara çizilen dikme, hem kenarortay, hem de açıortaydır.

5. Özellik

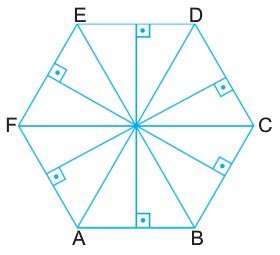
Bir düzgün çokgende kenar sayısı çift ise, çokgeni iki eş parçaya ayıran doğru parçaları simetri eksenidir.

Çözümlü Örnek Test Soruları

Soru 1
Bir çokgenin iç açılarının toplamı 1440° olduğuna göre, bu çokgen kaç kenarlıdır?

A) 8
B) 9
C) 10
D) 11
E) 12

Çözüm
Bir $n$ kenarlı çokgenin iç açılarının toplamı (n – 2) × 180 formülüyle bulunur.

(n – 2) × 180 = 1440
n – 2 = 1440 ÷ 180 = 8
n = 8 + 2 = 10

Cevap: C

Soru 2
Bir düzgün altıgenin bir iç açısının ölçüsü kaç derecedir?

A) 108°
B) 120°
C) 135°
D) 140°
E) 150°

Çözüm
Düzgün bir çokgenin bir iç açısının ölçüsü [(n – 2) × 180] ÷ n formülüyle bulunur.
Altıgen için n = 6 olduğundan:

[(6 – 2) × 180] ÷ 6 = (4 × 180) ÷ 6 = 120°

Cevap: B

Soru 3
Bir düzgün ongenin bir dış açısının ölçüsü kaç derecedir?

A) 30°
B) 36°
C) 40°
D) 45°
E) 50°

Çözüm
Düzgün bir çokgenin bir dış açısının ölçüsü 360° ÷ n formülüyle bulunur.
Ongen için n = 10 olduğundan:

360° ÷ 10 = 36°

Cevap: B

Soru 4
Bir düzgün sekizgenin bir iç açısının ölçüsü kaç derecedir?

A) 120°
B) 128.5°
C) 135°
D) 140°
E) 145°

Çözüm
Düzgün bir çokgenin bir iç açısının ölçüsü [(n – 2) × 180] ÷ n formülüyle bulunur.
Sekizgen için n = 8 olduğundan:

[(8 – 2) × 180] ÷ 8 = (6 × 180) ÷ 8 = 135°

Cevap: C

Soru 5
Bir düzgün yedigenin bir dış açısının ölçüsü kaç derecedir?

A) 45°
B) 51.4°
C) 54°
D) 60°
E) 72°

Çözüm
Düzgün bir çokgenin bir dış açısının ölçüsü 360° ÷ n formülüyle bulunur.
Yedigen için n = 7 olduğundan:

360° ÷ 7 ≈ 51.4°

Cevap: B

Soru 6
Bir düzgün dodekagonun (12 kenarlı çokgen) bir iç açısının ölçüsü kaç derecedir?

A) 130°
B) 140°
C) 144°
D) 150°
E) 156°

Çözüm
Düzgün bir çokgenin bir iç açısının ölçüsü [(n – 2) × 180] ÷ n formülüyle bulunur.
Dodekagon için n = 12 olduğundan:

[(12 – 2) × 180] ÷ 12 = (10 × 180) ÷ 12 = 150°

Cevap: D

Soru 7
Bir çokgenin dış açılarının toplamı kaç derecedir?

A) 180°
B) 270°
C) 360°
D) 540°
E) 720°

Çözüm
Herhangi bir çokgenin dış açılarının toplamı daima 360°’dir, kenar sayısından bağımsız olarak.

Cevap: C

Soru 8
Bir düzgün beşgenin bir iç açısının ölçüsü kaç derecedir?

A) 90°
B) 108°
C) 120°
D) 135°
E) 144°

Çözüm
Düzgün bir çokgenin bir iç açısının ölçüsü [(n – 2) × 180] ÷ n formülüyle bulunur.
Beşgen için n = 5 olduğundan:

[(5 – 2) × 180] ÷ 5 = (3 × 180) ÷ 5 = 108°

Cevap: B

Çokgenler konu anlatımı videosu konu başlıkları,

• Çokgen nedir, tanımı
• İç bükey (Konkav) çokgen ve Dış bükey (konveks) çokgen tanımları
• Çokgenlerin elemanları (Köşeleri, kenarları ve köşegenleri)
• Dış bükey çokgenin özellikleri (İç açıları toplamı, dış açıları toplamı, köşegenlerinin sayısı)
• Düzgün çokgenler ve özellikleri
• Bir çokgenin çizilebilme şartı
• Düzgün çokgenin alanı

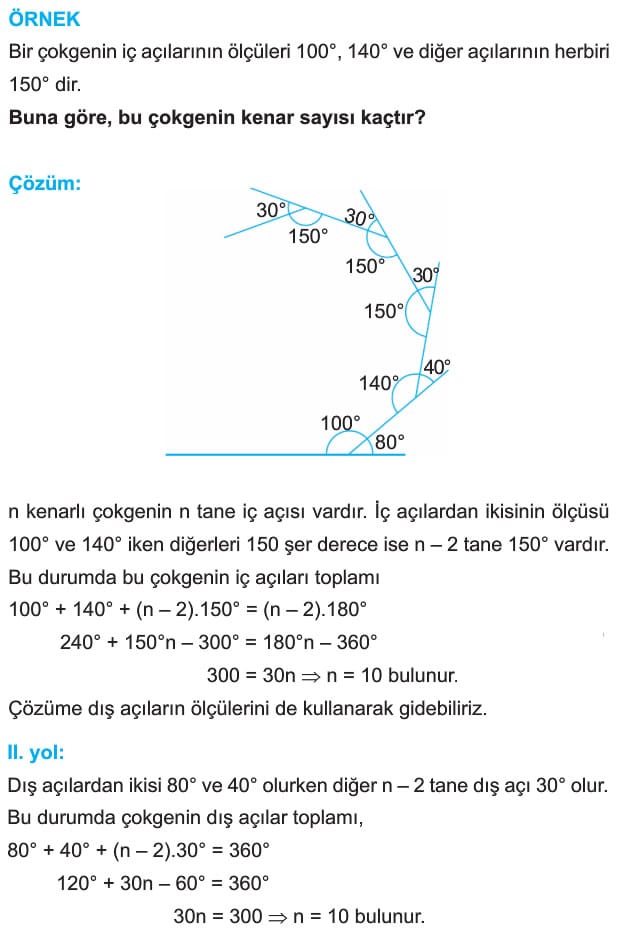
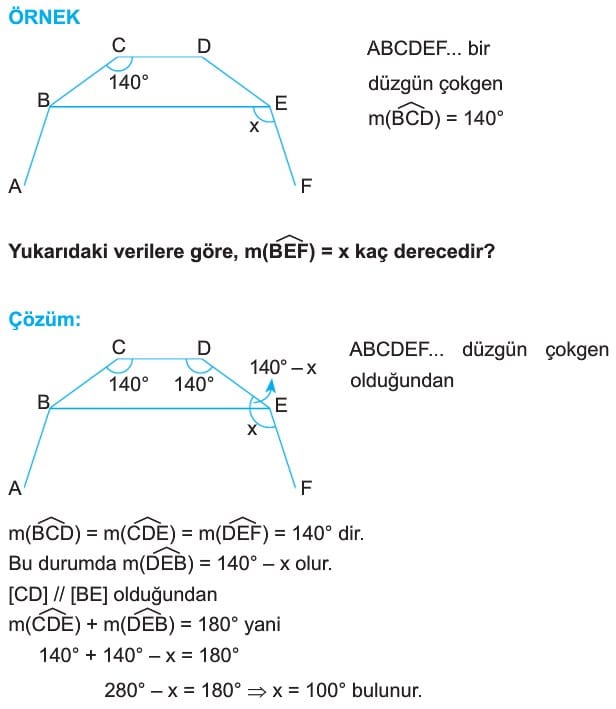
ÖRNEK: Bir çokgenin iç açılarının ölçüleri 1002 140” ve diğer açılarının her biri 150⁰ dir. Buna göre, bu çokgenin kenar sayısı kaçtır?
Çözüm: n kenarlı çokgenin n tane iç açısı vardır. İç açılardan ikisinin ölçüsü 100⁰ ve 140⁰ iken diğerleri 150 şer derece ise n – 2 tane 150⁰ vardır. Bu durumda bu çokgenin iç açıları toplamı 100° +140° + (n – 2).150° = (n – 2).180°
240⁰ + 150°n – 300⁰ =180°n – 360⁰
300 = 30n ise n = 10 bulunur.
Çözüme dış açıların ölçülerini de kullanarak gidebiliriz.
II. yol: Dış açılardan ikisi 80° ve 40° olurken diğer n – 2 tane dış açı 30° olur; Bu durumda çokgenin dış açılar toplamı,
80° + 40° + (n – 2).30° = 360°
120° + 30n – 60° = 360°
Son = 300 ise n = 10 bulunur.